2d-bicubic-interpolate 中文文档教程
2d-bicubic-interpolate
Ver. 1.0.7
此版本包括 Akshat Khare 的贡献。 根据 Akshat 拉取请求:
Previously the code failed for matrices with repeated value of z for
different record, which is undesired, so changed the code to accomodate
that issue.
Description
这个包是 cubic-spline 的简单实现,由 morganherlocker 用于双向插值(二维数组)。
此包的假定目的是插入两个变量的离散函数(例如,对于曲面图)。
z = f(x,y)
以下包是为另一个项目开发的,该项目利用它进行曲面图插值。
Dependencies
由于两个依赖项,程序包运行。 首先,当然是 cubic-spline by morganherlocker。 运行 2d-bicubic-spline 所需的另一个小包是 split-array,由 Arthur Verschaeve。 用于测试的开发依赖项包括 Mocha & 柴。
Install
安装包:
npm install --save 2d-bicubic-interpolate
Include in your project
import interpolateArray from '2d-bicubic-interpolate';
API
interpolateArray(data, n);
函数有两个参数:数据,包括要插值的数据集,以及描述插值“强度”的参数 n。 函数返回插值数据集。
data
数据集应该代表 离散函数 两个变量。 数据集应该是一个对象数组,其中每个对象都代表每个函数点的坐标。 坐标值应为实数。
const data = [
{
x: 0,
y: 0,
z: 2
},
{
x: 1,
y: 0,
z: 0.3
},
{
x: 0,
y: 1,
z: 1.4
},
{
x: 1,
y: 1,
z: 2.5
}
]
n parameter - the interpolation factor
插值因子,n参数需要是正整数或0。这个数字描述了多少个新点将被放置在主点之间。 例如,对于 n = 4,在输入数据的每 2 个主要点之间,将计算并插入四个新点。 对于 n = 0,不应用插值,输出与输入相同。
Output
函数 interpolateArray 返回新数据集,其结构与输入相同。 新数据数组的长度描述为:
L1 = L0 + (L0 - 1) * n
其中:
L1 - 输出数组的长度
L0 - 输入数组的长度
n - 插值因子
Examples
Example 1
import interpolateArray from '2d-bicubic-interpolate';
const data = [
{
x: 0,
y: 0,
z: 0.3
},
{
x: 1,
y: 0,
z: 1.2
},
{
x: 0,
y: 1,
z: 1.4
},
{
x: 1,
y: 1,
z: 2.2
}
];
console.log(interpolateArray(data, 1));
/*
console:
(9) [{…}, {…}, {…}, {…}, {…}, {…}, {…}, {…}, {…}]
0:{x: 0, y: 0, z: 0.3}
1:{x: 0, y: 0.5, z: 0.85}
2:{x: 0, y: 1, z: 1.4}
3:{x: 0.5, y: 0, z: 0.75}
4:{x: 0.5, y: 0.5, z: 1.275}
5:{x: 0.5, y: 1, z: 1.8}
6:{x: 1, y: 0, z: 1.2}
7:{x: 1, y: 0.5, z: 1.7}
8:{x: 1, y: 1, z: 2.2}
*/
Example 2
算法的工作原理由 3D 曲面图 (vis.js) 表示,表示一些双变量的离散函数。< br> 插值前数据:
InterpolateArray(data, 0);
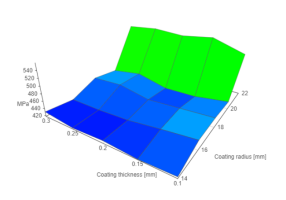
用不同插值因子插值的数据: 使用不同插值因子插值的数据:
InterpolateArray(data, 1);
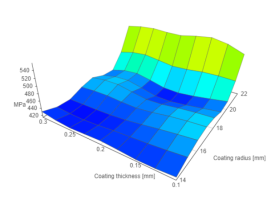
InterpolateArray(data, 10);
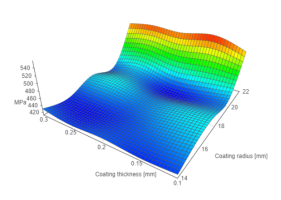
2d-bicubic-interpolate
Ver. 1.0.7
This version includes contribution of Akshat Khare. According to Akshat pull request:
Previously the code failed for matrices with repeated value of z for
different record, which is undesired, so changed the code to accomodate
that issue.
Description
This package is a simple implementation of a cubic-spline by morganherlocker for two-directional interpolation (2-dimensional arrays).
Assumed purpose of this package is to interpolate discrete function of two variables (e.g., for a surface plot).
z = f(x,y)
Following package was developed for another project that utilizes it for surface plot interpolation.
Dependencies
Package runs thanks to two dependencies. Firstly, of course cubic-spline by morganherlocker must be included. Another little package needed to run 2d-bicubic-spline is split-array by Arthur Verschaeve. Development dependencies fot testing include Mocha & Chai.
Install
To install package:
npm install --save 2d-bicubic-interpolate
Include in your project
import interpolateArray from '2d-bicubic-interpolate';
API
interpolateArray(data, n);
Function takes two parameters: data, including data set to interpolate, and parameter n that describes 'strength' of interpolation. Function returns interpolated data set.
data
Data set is expected to be representation of a discrete function of two variables. Data set is expected to be an array of objects, where every each object presents coordinates for each point of function. Coordinates values are expected to be real numbers.
const data = [
{
x: 0,
y: 0,
z: 2
},
{
x: 1,
y: 0,
z: 0.3
},
{
x: 0,
y: 1,
z: 1.4
},
{
x: 1,
y: 1,
z: 2.5
}
]
n parameter - the interpolation factor
Interpolation factor, the n parameter need to be a positive integer or 0. This number describes how many new points are going to be put between primary points. E.g., for n = 4, between every 2 primary points from input data, four new points are going to be calculated and inserted between. For n = 0, no interpolation is applied and output is the same as input.
Output
Function interpolateArray returns new data set, which has the same structure as an input. Length of new data array is described as:
L1 = L0 + (L0 - 1) * n
Where:
L1 - length of output array
L0 - length of input array
n - interpolation factor
Examples
Example 1
import interpolateArray from '2d-bicubic-interpolate';
const data = [
{
x: 0,
y: 0,
z: 0.3
},
{
x: 1,
y: 0,
z: 1.2
},
{
x: 0,
y: 1,
z: 1.4
},
{
x: 1,
y: 1,
z: 2.2
}
];
console.log(interpolateArray(data, 1));
/*
console:
(9) [{…}, {…}, {…}, {…}, {…}, {…}, {…}, {…}, {…}]
0:{x: 0, y: 0, z: 0.3}
1:{x: 0, y: 0.5, z: 0.85}
2:{x: 0, y: 1, z: 1.4}
3:{x: 0.5, y: 0, z: 0.75}
4:{x: 0.5, y: 0.5, z: 1.275}
5:{x: 0.5, y: 1, z: 1.8}
6:{x: 1, y: 0, z: 1.2}
7:{x: 1, y: 0.5, z: 1.7}
8:{x: 1, y: 1, z: 2.2}
*/
Example 2
Working principle of algorithm is presented by a 3D surface chart (vis.js), representing some discrete function of two-variables.
Data before interpolation:
InterpolateArray(data, 0);

Data interpolated with different interpolation factors: Data interpolated with different interpolation factors:
InterpolateArray(data, 1);

InterpolateArray(data, 10);

你可能也喜欢
- 3d-viewer-vue 中文文档教程
- 7-segment-timer.contracts 中文文档教程
- @1mmunity/discord-bot-base 中文文档教程
- @1ncounter/vue-cli-plugin-mock 中文文档教程
- @3ddie/react-native-calendars 中文文档教程
- @_mehrad/ngx-daterangepicker-material 中文文档教程
- @aaas/file-set 中文文档教程
- @abcnews/dev-proxy 中文文档教程
- @abear/hweb-tools 中文文档教程
- @abizzle/eslint-config-abizzle 中文文档教程
