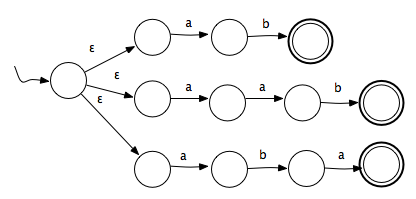
如何将 (ab u aab u aba)* 转换为 NFA?
(ab u aab u aba)*
我做到了,但我想要一些关于其正确性的反馈:
如果正确:我们可以进一步简化 (ab u aab u aba)* 吗?
如果没有:我错过了什么?
编辑:看来我缺少从所有 3 个最终状态回到初始状态的电子转换,我需要一个初始和最终的新状态,它将在电子转换时转到旧的初始状态。 (克莱恩星规则)。
PS 我们还可以简化 (aub)*aabab 和 ( aub)*a(aub)(aub)(aub)(aub)。
我之所以问这个问题,是因为如果没有办法简化/最小化,这将是一个长得可笑的 DFA...
(ab u aab u aba)*
I did it but I would like some feedback on its correctness:
If it is correct: Can we simplify (ab u aab u aba)* any further?
If not: What did I miss?
EDIT: It seems I am missing e-transitions from all 3 final states back to the initial state and I need a new state that is initial and final which will go to the old initial state on e-transition. (Kleene Star rule).

P.S. Can we also simplify (a u b)*aabab and (a u b)*a(a u b)(a u b)(a u b)(a u b).
The reason why I ask because if there's no way to simplify/minimize, it will be a ridiculously long DFA...
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(1)
我可以看到您的第一个案例的一个小简化,您可以将其写为 (a(bu ab u ba))* 但这不一定有帮助。我仍然猜测您的 DFA 不需要您想象的那么多状态。
后两种情况都需要具有 32 个状态的 DFA,以便跟踪最后读取的 5 个字符。不同之处在于,第二个 DFA 只有 1 个终止状态,而第三个 DFA 有 16 个。
I can see a small simplification of your first case in that you can write it as (a(b u ab u ba))* but that doesn't necessarily help. I would still guess that your DFA won't need as many states as you think.
Both of the latter cases will need DFAs with 32 states in order to keep track of the last 5 characters read. The difference is that the second DFA only has one terminal state while the third DFA has 16.