如何使用运算符(或其他东西)编写 NNN .... N ?
嗯..我从昨天开始学习APL。我正在观看 YouTube 视频,从基础开始教授各种符号,并且我正在使用 NARS2000。
我想要的是打印斐波那契数列。我知道有几个代码,但是由于我没有研究过高级的东西,所以我开始编写自己的代码。
首先我制作了这个数组: 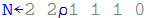
这个想法很简单:Nⁿ 中 (1,1) 处的元素是第 (n+1) 个斐波那契序列。
我所做的是:
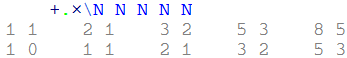
和
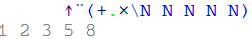
好吧,它有效。但是,如果我想要第 16 个学期,那么我应该这样做
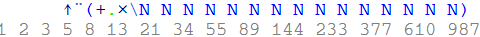
我需要的是写入任意数量的Ns。我当然知道{rho}。然而,

(底部被切掉)
我注意到 (i 2 2 ){rho}N 和 i Ns 不同。
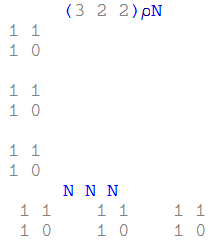
我应该使用什么运算符来执行与 NN N...N 相同的操作?
Well.. I have started to learn APL since yesterday. I'm watching youtube videos teaching about various symbols from basic, and I'm using NARS2000.
What I want is to print the Fibonacci sequence. I know there's several codes, but since I haven't studied advanced things, I started to write my own code.
First I made this array: 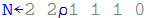
The idea is simple : the element at (1,1) in Nⁿ is (n+1)th fibonacci sequence.
What I did was:
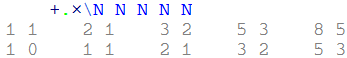
and
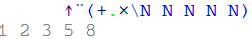
Well, it works. However, if I want 16th term, then I should do
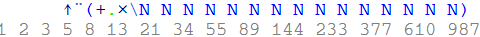
What I need is to write arbitary amount of Ns. Of course I know about {rho}. However,

(bottom was cut)
And I noticed that (i 2 2){rho}N and i Ns are different.
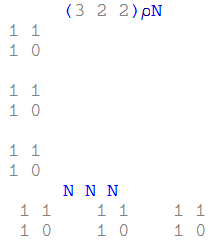
What operator I should use to do same thing as N N N...N does?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
你就快到了。
⍴(“重塑”)是正确的运算符;但是,您希望它将矩阵 N 视为单个标量元素,而不是矩阵。为此,您可以使用“enclose”运算符⊂将其包装起来:如果我们将其包装起来,我们会得到(例如)以下内容表达式:(
不过,请允许我说一句:根据定义,斐波那契数列以
0和1开头。)You were almost there.
⍴("reshape") is the right operator to use; however, you want it to treat your matrix N not as a matrix, but as a single, scalar element. For this purpose, you wrap it using the "enclose" operator⊂:If we wrap this up, we arrive at (e.g.) the following expression:
(Allow me one remark, though: by definition, the Fibonacci sequence starts with
0and1.)如果你想从 0 和 1 开始,只需使用 0 1 1 1 而不是 1 1 1 0
If you want to start with 0 and 1, just use 0 1 1 1 instead of 1 1 1 0