Mathematica 对 #^2 和 #^2 的令人费解的解释/@范围[n]

发布于 2024-12-09 21:08:46 字数 681 浏览 2 评论 0原文

我对 Mathematica 对以下内容的回应感到困惑：

ClearAll[n]
#^2 & /@ Range[n]
#^2 & /@ Range[n] // StandardForm

Range1

似乎连 Mathematica (8.0) 也不相信它是什么刚刚说过：

#^2 & /@ Range[5]
Range[5^2]

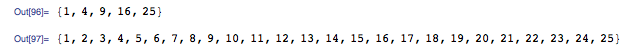
Range2

对正在发生的事情有什么想法吗？

编辑：

此问题的原始上下文如下。我已经写过

PrimeOmega[Range[n]] - PrimeNu[Range[n]]

，由于 n 将会非常大（2^50），我想我可以通过将其重写为来节省时间：

 PrimeOmega[#] - PrimeNu[#] &/@Range[n]

回想起来，这可能不是一个好主意。（我可以使用 Module 来“计算”范围一次。）

原文

I'm puzzled by Mathematica's responses to the following:

ClearAll[n]
#^2 & /@ Range[n]
#^2 & /@ Range[n] // StandardForm

Range1

It seems that even Mathematica (8.0) doesn't believe what it has just said:

#^2 & /@ Range[5]
Range[5^2]

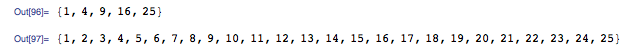
Range2

Any thoughts about what is happening?

Edit:

The original context for this question was the following. I had written

PrimeOmega[Range[n]] - PrimeNu[Range[n]]

and since n was going to be very large (2^50), I thought I might save time by rewriting it as:

 PrimeOmega[#] - PrimeNu[#] &/@Range[n]

Thinking back, that probably wasn't such a good idea. (I could have used Module to 'compute' the Range only once.)

分享到QQ

分享到微博

如果你对这篇内容有疑问，欢迎到本站社区发帖提问参与讨论，获取更多帮助，或者扫码二维码加入 Web 技术交流群。

发布评论

需要登录才能够评论，你可以免费注册一个本站的账号。

花开雨落又逢春i 2024-12-16 21:08:46

由于 n 未定义，因此 Range[n] 计算为自身。因此，Map 对它的作用就像对任何其他符号头一样，将您的函数映射到其元素上 - 这里它只是 n

In[11]:= #^2 & /@ someHead[n]
Out[11]= someHead[n^2]

EDIT

解决问题在您的编辑中 - 对于数字 n，Range 可以计算为列表，并且您会得到预期的结果（即 Range[5]^2< /code> 都是关于求值的顺序的。 Range[5^2]，您可以使用 #^2&/@Unevaluated[Range[5]]，在这种情况下，一切都会像符号一样发生>n 上面）。事实上，Range 在非数字输入时发出错误消息。另外，它与问题无关，但像 #^2& 这样的函数是 Listable 的，您不必映射它们。

Since n is undefined, Range[n] evaluated to itself. Therefore, Map acts on it as on any other symbolic head, mapping your function on its elements - here it is just n

In[11]:= #^2 & /@ someHead[n]
Out[11]= someHead[n^2]

EDIT

Addressing the question in your edit - for numeric n, Range evaluates to a list all right, and you get the expected result (which is, Range[5]^2. It is all about the order of evaluation. To get Range[5^2], you could have used #^2&/@Unevaluated[Range[5]], in which case everything happens just like for symbolic n above) . In fact, Range issues an error message on non-numeric input. Also, it is tangential to the question, but functions like #^2& are Listable, and you don't have to map them.

回复收藏 0 原文

弃爱 2024-12-16 21:08:46

有点偏离主题，但您可以通过根据 FactorInteger 重新定义来提高速度，然后每个输入仅调用一次。

f1[n_] := PrimeOmega[Range[n]] - PrimeNu[Range[n]]
f2[n_] := With[{fax=FactorInteger[#]}, Total[fax[[All,2]]]-Length[fax]]& /@ Range[n]

示例：

In[27]:= Timing[pdiff1 = f1[2^20];]
Out[27]= {37.730264, Null}

In[28]:= Timing[pdiff2 = f2[2^20];]
Out[28]= {9.364576, Null}

In[29]:= pdiff1===pdiff2
Out[29]= True

丹尼尔·利希特布劳

Slightly off topic, but you can improve the speed by redefining in terms of FactorInteger, which then is only called once per input.

f1[n_] := PrimeOmega[Range[n]] - PrimeNu[Range[n]]
f2[n_] := With[{fax=FactorInteger[#]}, Total[fax[[All,2]]]-Length[fax]]& /@ Range[n]

Example:

In[27]:= Timing[pdiff1 = f1[2^20];]
Out[27]= {37.730264, Null}

In[28]:= Timing[pdiff2 = f2[2^20];]
Out[28]= {9.364576, Null}

In[29]:= pdiff1===pdiff2
Out[29]= True

Daniel Lichtblau

回复收藏 0 原文

~没有更多了~