如何从显式方程构造多边形?
假设我有一个可以在 OpenGL 中表示对象形状的显式方程,我应该如何从显式方程中“绘制”出形状?
例如,我有这个显式方程: 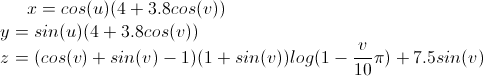
u 和 v 都是实数。
然后我尝试在 OpenGL C++ 中执行此操作:
float maxParts = 20;
vector<float> point(3);
glBegin(GL_QUAD_STRIP);
for(int i=0; i<=maxParts; i++) {
float u = ((float)i/maxParts)*2*M_PI;
for(int j=-maxParts; j<=maxParts; j++) {
float v = (j/maxParts) * M_PI;
point[0] = cos(u) * (4.0+3.8*cos(v));
point[1] = sin(u) * (4.0+3.8*cos(v));
point[2] = (cos(v) + sin(v) - 1.0) * (1.0 + sin(v)) * log(1.0-M_PI*v/10.0) + 7.5 * sin(v);
glVertex3f(point[0], point[1], point[2]);
}
}
glEnd();
但事实证明它真的很糟糕。上面的代码对形状有些许印象,但多边形渲染不正确。我应该如何迭代 x、y 和 z 坐标的显式方程以根据方程构造形状?
Suppose I have an explicit equation that could represent an object shape in OpenGL, how should I sort of "plot" out the shape from the explicit equation?
For example, I have this explicit equation: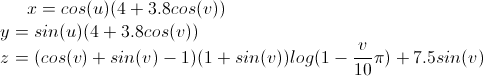
Both u and v are members of the real numbers.
I then tried to do this in OpenGL C++:
float maxParts = 20;
vector<float> point(3);
glBegin(GL_QUAD_STRIP);
for(int i=0; i<=maxParts; i++) {
float u = ((float)i/maxParts)*2*M_PI;
for(int j=-maxParts; j<=maxParts; j++) {
float v = (j/maxParts) * M_PI;
point[0] = cos(u) * (4.0+3.8*cos(v));
point[1] = sin(u) * (4.0+3.8*cos(v));
point[2] = (cos(v) + sin(v) - 1.0) * (1.0 + sin(v)) * log(1.0-M_PI*v/10.0) + 7.5 * sin(v);
glVertex3f(point[0], point[1], point[2]);
}
}
glEnd();
But it turns out to be just really crappy. The above code somewhat gives a slight impression of the shape but the polygons are not rendered properly. How should I iterate through the explicit equation for the x, y and z coordinates to construct the shape from the equation?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(1)
一般来说,你会朝着正确的方向前进。然而,您错过了关键的步骤,您必须将补丁分割成更小的四边形(将其细分)。因此,您不仅要迭代采样点,还要迭代补丁,并且必须为每个补丁生成 4 个采样点。
您还需要提供顶点法线。顶点法线由向量 δ{x,y,z}/δu 和 δ{x,y,z}/δv 的叉积给出
根据评论进行编辑
用于发出独立四边形的代码示例:
You're generally going into the right direction. However you missed the crucial step, that you'll have to split down the patch into smaller quads (tesselate it). So you don't just iterate over the sampling points, you iterate over the patches and must generate 4 sampling points for each patch.
Also you need to supply the vertex normals. The vertex normals are given by taking the cross product of the vectors δ{x,y,z}/δu and δ{x,y,z}/δv
EDIT due to comment
Code example for emitting independent quads: