食物网中的营养位置/高度（遵循网络中的路径）

Question

作为为我正在开发的包开发演示的一部分，我需要量化经典的生态食物网，如下所述。我已经检查过纯素、双向和 sna，但没有看到任何能满足我需要的东西，尽管我可能是错的 - 这些都是大包。因此，我想知道这个想法是否已经包含在包中，或者是否有人有一个聪明的方法来计算结果。看起来应该是一个包。

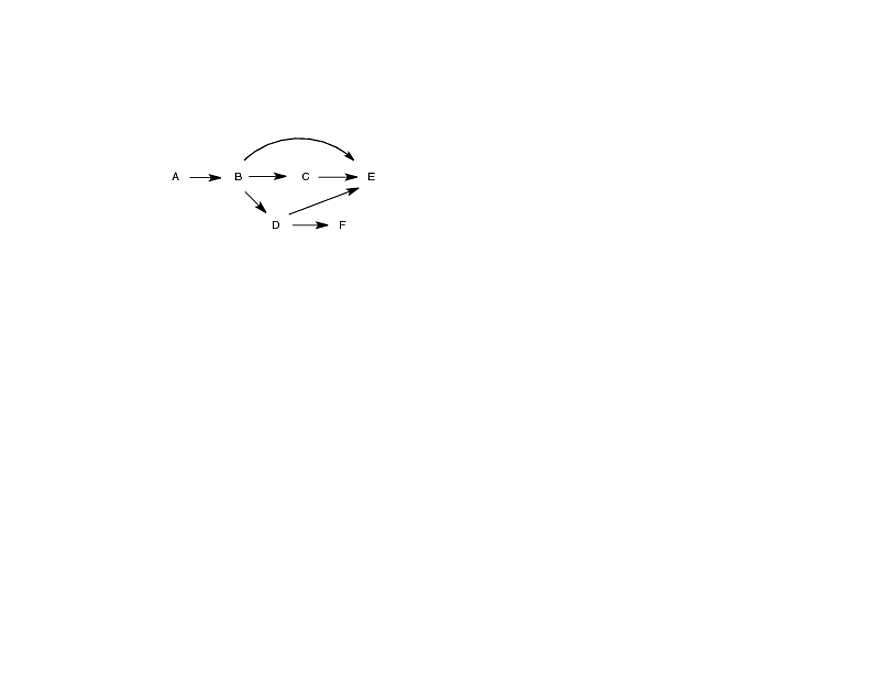
食物网可以通过物种 A:F 之间的相互作用矩阵来描述，如代码和图表所示。用语言来说，人们会说“A吃B，B又吃E”等等（在矩阵中很难看出，在图中微不足道）。

species <- LETTERS[1:6]

links <- c(0, 1, 0, 0, 0, 0,
    1, 0, 1, 1, 1, 0,
    0, 1, 0, 0, 1, 0,
    0, 1, 0, 0, 1, 1,
    0, 1, 1, 1, 0, 0,
    0, 0, 0, 1, 0, 0)

L <- matrix(links, nrow = 6, byrow = TRUE,
    dimnames = list(species, species))

我想计算每个物种的营养位置和营养高度。营养级位置定义为食物链中特定物种以下的物种总数 + 1。在图中，A 的营养级位置为 6，D 的营养级位置为 3。另一方面，营养级高度是平均值物种在其参与的每个单独链中的位置。物种B连接到4条不同的链（路径）；它的高度是一次考虑的位置的平均值：(3 + 3 + 3 + 2)/4 = 2.75。

在计算上，需要读取矩阵 L，然后通过矩阵隐含的不同路径来计算所需的值。

如果这不是太迟钝，有谁知道一个可以做到这一点的包，或者找到一种遵循路径并计算各种长度/选项的方法？它“感觉”好像必须有一些递归/应用方法应该有效，但我不想重新发明东西。

提前致谢

Answer 1

这是经典的图论内容。你所拥有的是一个有向图，其中动物是节点，“A 吃 B”是边。那么你的矩阵就是一个对边进行编码的邻接矩阵（但你可能希望矩阵的一半为0，所以你不会让A吃B而B吃A。类似地，对角线上的零，除非你有同类相食行为）。这是另一个答案中链接的有向无环图。

图论包在图形模型任务视图中列出：

http://ftp.heanet.ie/mirrors/cran.r-project.org/web/views/gR.html

我认为 igraph 会做你想做的。首先从你的矩阵中创建一个图形对象（使用仅包含上三角形的修改后的矩阵）：

> LG=graph.adjacency(L)
> LG
Vertices: 6 
Edges: 7 
Directed: TRUE 
Edges:

[0] 'A' -> 'B'
[1] 'B' -> 'C'
[2] 'B' -> 'D'
[3] 'B' -> 'E'
[4] 'C' -> 'E'
[5] 'D' -> 'E'
[6] 'D' -> 'F'

然后你可以使用neighborhood.size来获取营养位置：

> neighborhood.size(LG,Inf,mode="out")
[1] 6 5 2 3 1 1

其顺序应该是A，B，C，D，E，F。请注意，使用 Inf 来停止限制邻域，并使用 mode="out" 来仅沿着吃的方向遵循图形边缘。

所有关于食物链的讨论都让我感到饥饿。希望这能让你开始。

巴里

Answer 2

这是计算您所追求的营养高度的一种方法。

假设矩阵 L 编码 DAG ，其中从每行中的物种到每列中的物种的链接。
L_(i,j)=1 表示 spp_i 吃 spp_j。

那么L*L表示连接每对物种的两步“营养路径”的数量，L*L*L包含三步路径的数量，等等在。在它们之间，“矩阵幂”集记录了连接节点对的所有路径，无论长度如何。

根据您的描述，一个物种的营养高度是一加上将其连接到图表尖端的“叶节点”之一的所有路径的平均路径长度。

## Here I've edited the matrix L to make it a DAG
species <- LETTERS[1:6]

links <-
  c(0, 1, 0, 0, 0, 0,
    0, 0, 1, 1, 1, 0,
    0, 0, 0, 0, 1, 0,
    0, 0, 0, 0, 1, 1,
    0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0)

L <- matrix(links, nrow = 6, byrow = TRUE,
    dimnames = list(FROM=species, TO=species))

此函数（使用 expm 包中的运算符）应该可以满足您的要求。它可以做一些更详细的评论，但如果我有时间，我会在稍后添加。

library(expm) ## provides "%^%", a matrix power operator

calcHeight <- function(MAT) {
    ## Find 'leaf nodes' (i.e. species that are only eaten,
    ## and don't eat any others)
    leaves <- which(rowSums(L)==0)

    ## Find the maximum possible chain length (if this is a DAG)
    maxHeight <- nrow(MAT) - length(leaves) - 1
    ## Then use it to determine which matrix powers we'll need to calculate.
    index <- seq_len(maxHeight)

    paths <- lapply(index, FUN=function(steps) MAT %^% steps)
    pathSteps <- lapply(index, FUN=function(steps) (1 + steps) * paths[[steps]])

    ## Trophic height is expressed relative to leaf nodes
    paths <- Reduce("+", paths)[-leaves, leaves]
    pathSteps <- Reduce("+", pathSteps)[-leaves, leaves]

    rowSums(pathSteps)/rowSums(paths)
}

calcHeight(L)
   A    B    C    D 
3.75 2.75 2.00 2.00