如何在 scipy 创建的树状图中获得与颜色簇相对应的平面聚类

Question

使用发布的代码 在这里，我创建了一个很好的层次聚类：

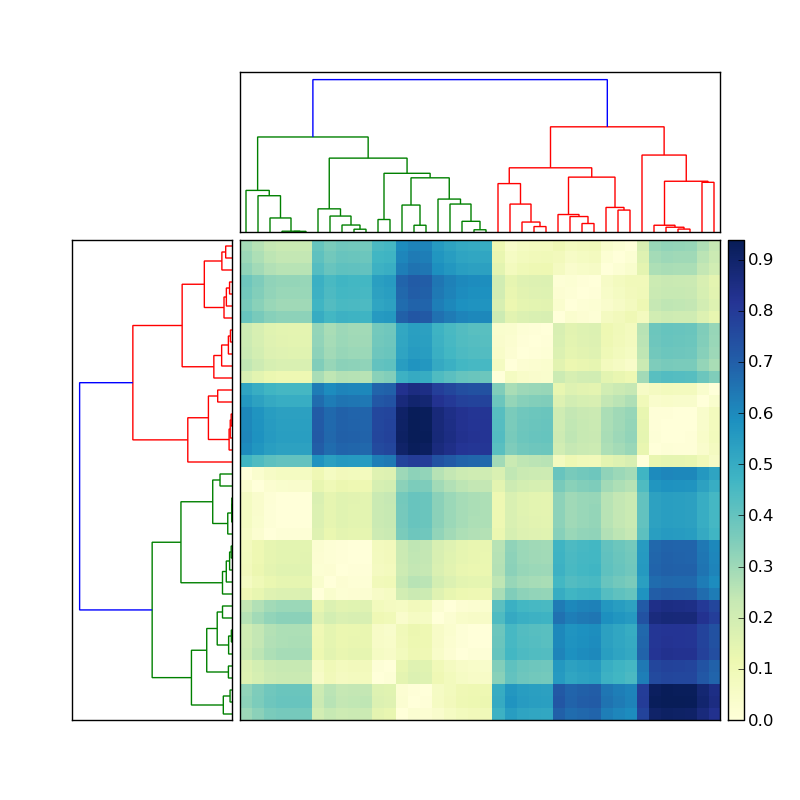
假设左侧的树状图是通过执行以下操作创建的

Y = sch.linkage(D, method='average') # D is a distance matrix
cutoff = 0.5*max(Y[:,2])
Z = sch.dendrogram(Y, orientation='right', color_threshold=cutoff)

：现在如何获取每个彩色簇的成员的索引？ 为了简化这种情况，忽略顶部的聚类，仅关注矩阵左侧的树状图。

此信息应存储在树状图 Z 存储变量中。有一个函数应该可以做我想要的事情，称为fcluster（请参阅文档此处）。但是，我看不到在哪里可以为 fcluster 提供与我在创建树状图时指定的相同的 cutoff。看来 fcluster 中的阈值变量，t 必须根据各种模糊的测量值（不一致不一致，距离>、maxclust、monocrit）。有什么想法吗？

Answer 1

我认为你走在正确的道路上。让我们试试这个：

import scipy
import scipy.cluster.hierarchy as sch
X = scipy.randn(100, 2)     # 100 2-dimensional observations
d = sch.distance.pdist(X)   # vector of (100 choose 2) pairwise distances
L = sch.linkage(d, method='complete')
ind = sch.fcluster(L, 0.5*d.max(), 'distance')

ind 将为您提供 100 个输入观测值中每个观测值的聚类索引。 ind 取决于您在 linkage 中使用的方法。尝试 method=single、complete 和 average。然后注意 ind 有何不同。

示例：

In [59]: L = sch.linkage(d, method='complete')

In [60]: sch.fcluster(L, 0.5*d.max(), 'distance')
Out[60]: 
array([5, 4, 2, 2, 5, 5, 1, 5, 5, 2, 5, 2, 5, 5, 1, 1, 5, 5, 4, 2, 5, 2, 5,
       2, 5, 3, 5, 3, 5, 5, 5, 5, 5, 5, 5, 2, 2, 5, 5, 4, 1, 4, 5, 2, 1, 4,
       2, 4, 2, 2, 5, 5, 5, 2, 5, 5, 3, 5, 5, 4, 5, 4, 5, 3, 5, 3, 5, 5, 5,
       2, 3, 5, 5, 4, 5, 5, 2, 2, 5, 2, 2, 4, 1, 2, 1, 5, 2, 5, 5, 5, 1, 5,
       4, 2, 4, 5, 2, 4, 4, 2])

In [61]: L = sch.linkage(d, method='single')

In [62]: sch.fcluster(L, 0.5*d.max(), 'distance')
Out[62]: 
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1])

scipy.cluster.hierarchy 确实令人困惑。在你的链接中，我什至不认识我自己的代码！

Answer 2

我编写了一些代码来解压缩链接矩阵。它返回一个字典，其中包含按每个聚合步骤分组的标签索引。我只在complete链接集群的结果上进行了尝试。字典的键从 len(labels)+1 开始，因为最初，每个标签都被视为自己的簇。这可能会回答你的问题。

import pandas as pd
import numpy as np
from scipy.cluster.hierarchy import linkage

np.random.seed(123)
labels = ['ID_0','ID_1','ID_2','ID_3','ID_4']

X = np.corrcoef(np.random.random_sample([5,3])*10)
row_clusters = linkage(x_corr, method='complete')    

def extract_levels(row_clusters, labels):
    clusters = {}
    for row in xrange(row_clusters.shape[0]):
        cluster_n = row + len(labels)
        # which clusters / labels are present in this row
        glob1, glob2 = row_clusters[row, 0], row_clusters[row, 1]

        # if this is a cluster, pull the cluster
        this_clust = []
        for glob in [glob1, glob2]:
            if glob > (len(labels)-1):
                this_clust += clusters[glob]
            # if it isn't, add the label to this cluster
            else:
                this_clust.append(glob)

        clusters[cluster_n] = this_clust
    return clusters

返回：

{5: [0.0, 2.0],
 6: [3.0, 4.0],
 7: [1.0, 0.0, 2.0],
 8: [3.0, 4.0, 1.0, 0.0, 2.0]}

Answer 3

我知道这对游戏来说已经很晚了，但是我根据帖子 此处。它已在 pip 上注册，因此要安装，您只需调用

pip install pydendroheatmap

此处查看该项目的 github 页面：https://github。 com/themantalope/pydendroheatmap

Answer 4

您还可以尝试 cut_tree，它有一个高度参数，可以为您提供超测量所需的信息。