寻找直线交点的算法
我在某处看到了一个关于线路交叉的问题并试图解决。
有一个 8 位像素的 64x64 网格,上面有一堆 1 像素宽的不同颜色的垂直和水平线。所有平行线之间至少有一个空格。问题是找出每组彩色线所产生的线交叉数量(例如,所有绿线交叉都计为一个总和)。并找出哪一组线的交叉次数最少。此外,同一颜色的所有垂直线的尺寸相同,并且同一颜色的所有水平线的尺寸相同。
我有一些想法,但它们似乎都效率很低。这将涉及到遍历网格中的每个像素,如果遇到颜色,请确定它是垂直线还是水平线,然后一直沿着该线的方向前进,同时检查相邻边是否有不同颜色。
我正在尝试确定首先计算每种颜色的水平线和垂直线的长度是否会加快该过程。你们对于如何做到这一点有什么绝妙的想法吗?
这里有两个例子。请注意,平行线之间始终有一个空格。

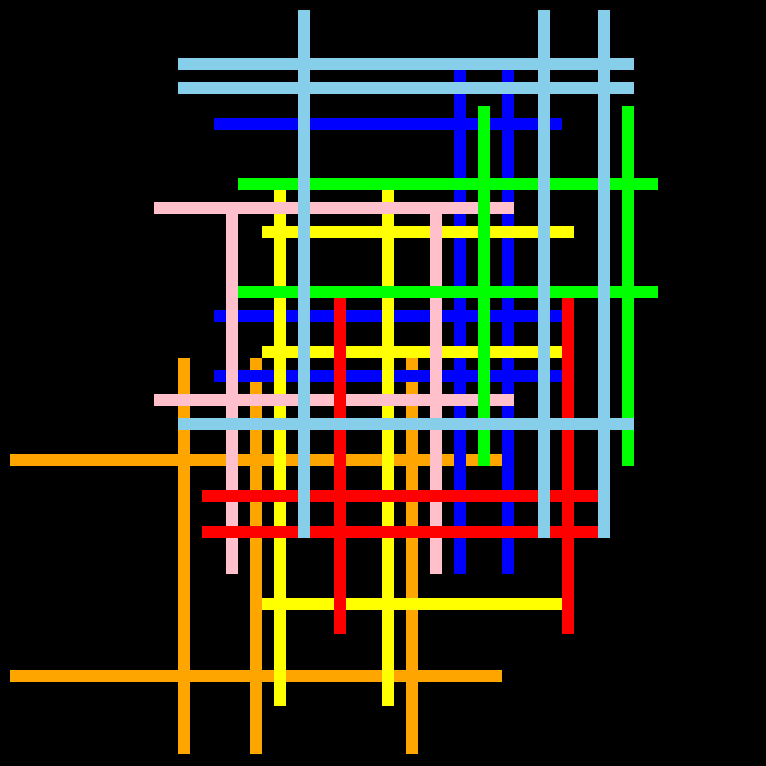
there's this problem about line crossings I saw somewhere and was trying to solve.
There's a 64x64 grid of 8 bit pixels and it has a bunch of 1 pixel wide vertical and horizontal lines of different colors on it. All parallel lines have at least one space between them. The problem is to find the number of line crossings that each set of colored lines makes (e.g. all green line crossings count towards one sum). And find which set of lines had the fewest amount of crossings. Also, all vertical lines of a color are the same size and all horizontal lines of the same color are the same size.
I had a few ideas but they all seem pretty inefficient. It would involve going through every pixel in the grid, if you run into a color determine if it's a vertical or horizontal line, and then go in the direction of the line all the while checking adjacent sides for different colors.
I'm trying to decide if first counting the length of the horizontal and vertical lines for each color would speed up the process. Do you guys have any brilliant ideas for how to do this?
Here are two examples. Notice that parallel lines always have a space in between them.


如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(4)
在带有线条的网格上寻找 2 种 3x3 方块:
“.”代表背景(总是黑色?),“a”和“b”代表2种不同的颜色(也不同于背景颜色)。如果找到,则将 a 色线交叉点和 b 色线交叉点的计数增加 1。
On the grid with your lines look for 2 types of 3x3 squares:
"." represents background (always black?), "a" and "b" represent 2 different colors (also different from the background color). If found, bump up by 1 the counts for a-colored line intersections and b-colored line intersections.
扫描像素网格实际上非常快速且高效。计算机视觉系统执行此类操作是标准的。许多此类扫描都会生成经过 FIR 滤波的图像版本,强调所搜索的细节类型。
主要技术术语是“卷积”(参见http://en.wikipedia.org/wiki/Convolution)。我认为它是一种加权移动平均线,尽管权重可能是负数。维基百科上的动画显示了使用相当无聊的脉冲(它可能是更有趣的形状)和一维信号(如声音)而不是二维(图像)信号的卷积,但这是一个非常普遍的概念。
人们很容易认为,通过避免提前计算过滤版本可以完成更有效的事情,但这样做的通常效果是,因为您没有预先计算所有这些像素,所以最终会多次计算每个像素。换句话说,将过滤后的图像视为基于查找表的优化,或者一种动态编程。
其速度快的一些特殊原因是...
另一个优点是您只需要编写一个图像过滤卷积函数。特定于应用程序的部分是如何定义过滤器内核,它只是权重值的网格。事实上,您可能根本不应该自己编写这个函数 - 各种数字代码库可以提供高度优化的版本。
为了处理不同颜色的线条,我只需首先为每种颜色生成一个灰度图像,然后分别过滤和检查每个颜色。再次,将此视为优化 - 尝试避免生成单独的图像可能会导致更多的工作,而不是更少。
您可以基于以下 FIR 滤波器内核进行卷积...
点为零(与像素无关),或者可能为负值(更喜欢黑色)。星号是正值(首选白色)。也就是说,寻找交叉点处的三乘三十字。
然后,您扫描过滤后的结果,寻找比某个阈值更亮的灰度像素 - 与您的图案最匹配的像素。如果您确实只想要精确的交叉点,您可能只接受完美匹配的颜色,但您可能需要考虑 T 型连接等。
Scanning a pixel grid is actually very fast and efficient. It's standard for computer vision systems to do that kind of thing. A lot of these scans produce a FIR filtered versions of images that emphasize the kinds of details being searched for.
The main technical term is "convolution" (see http://en.wikipedia.org/wiki/Convolution). I think of it as a kind of weighted moving average, though weights can be negative. The animations on Wikipedia show convolution using a rather boring pulse (it could have been a more interesting shape), and on a 1D signal (like a sound) rather than a 2D (image) signal, but this is a very general concept.
It's tempting to think that something more efficient can be done by avoiding calculating that filtered version in advance, but the usual effect of that is that because you haven't precalculated all those pixels, you end up calculating each pixel several times. In other words, think of the filtered image as a lookup-table based optimisation, or a kind of dynamic programming.
Some particular reasons why this is fast are...
Another advantage is that you only need to write one image-filtering convolution function. The application-specific part is how you define the filter kernel, which is just a grid of weight values. In fact you probably shouldn't write this function yourself at all - various libraries of numeric code can supply highly optimised versions.
For handling the different colours of lines, I'd simply generate one greyscale image for each colour first, then filter and check each separately. Again, think of this as the optimisation - trying to avoid generating the separate images will likely result in more work, not less.
You could do a convolution that based on the following FIR filter kernel...
Dots are zeros (pixel irrelevant) or, possibly, negative values (prefer black). Asterisks are positive values (prefer white). That is, look for the three-by-three crosses at the intersections.
Then you scan the filtered result looking for greyscale pixels that are brighter than some threshold - the best matches for your pattern. If you really only want exact crossing points, you may only accept the perfect-match colour, but you might want to make allowances for T-style joins etc.
您唯一的输入是 64x64 网格吗?如果是这样,那么您正在寻找具有 64x64 风格的内容,因为没有其他方法可以确保您发现了所有行。因此,我假设您正在谈论操作级别的优化,而不是渐近的优化。我似乎记得旧的“图形宝石”系列有很多这样的例子,重点是减少指令数量。我自己更擅长渐近问题,但这里有一些小想法:
网格单元具有 grid[i,j] 是绿色交集的属性,如果
因此您只需扫描数组一次,而不必担心显式检测水平和垂直线...只需使用这种关系遍历它并在找到交叉点时计算出交叉点。所以至少您只使用了一个具有相当简单逻辑的 64x64 循环。
由于没有两条平行线直接相邻,因此您知道当您经过已填充的单元格时,可以将内循环计数器增加 2。这将为您节省一些工作。
根据您的架构,您可能有一种快速的方法来对整个网格与其自身的偏移副本进行 AND 运算,这将是计算上述交集公式的一种很酷的方法。但是,您仍然必须遍历整个过程才能找到剩余的填充单元格(即交叉点)。
即使您没有图形处理器之类的东西来让您对整个网格进行“与”操作,如果颜色数量小于字号的一半,您也可以使用这个想法。例如,如果您有 8 种颜色和 64 位机器,那么您可以将 8 个像素填充到一个无符号整数中。所以现在你可以一次对8个网格单元进行外循环比较操作。这可能会为您节省大量工作,值得进行两次遍历,一次用于水平外循环,一次用于垂直外循环。
Is your only input the 64x64 grid? If so, then you're looking at something with a 64x64 flavor, since there's no other way to ensure you've discovered all the lines. So I will assume you're talking about optimizing at the operation level, not asymptotically. I seem to remember the old "Graphics Gems" series had lots of examples like this, with an emphasis on reducing instruction count. I'm better at asymptotic questions myself, but here are a few small ideas:
The grid cells have the property that grid[i,j] is a green intersection if
So you can just scan the array once, without worrying about explicitly detecting horizontal and vertical lines ... just go through it using this relationship and tally up intersections as you find them. So at least you're just using a single 64x64 loop with fairly simple logic.
Since no two parallel lines are directly adjacent, you know you can bump your inner loop counter by 2 when you pass a populated cell. That'll save you a little work.
Depending on your architecture, you might have a fast way to AND the whole grid with offset copies of itself, which would be a cool way to compute the above intersection formula. But then you still have to iterate through the whole things to find the remaining populated cells (which are the intersection points).
Even if you don't have something like a graphics processor that lets you AND the whole grid, you can use the idea if the number of colors is less than half of your word size. For example, if you have 8 colors and a 64-bit machine, then you can cram 8 pixels into a single unsigned integer. So now you can do the outer loop comparison operation for 8 grid cells at a time. This might save you so much work it's worth doing two passes, one for a horizontal outer loop and one for a vertical outer loop.
找到直线交叉点的简单方法
Simple way to find straight intersection