我想编写一个广泛使用 BLAS 和 LAPACK 线性代数功能的程序。由于性能是一个问题,我做了一些基准测试,想知道我采取的方法是否合法。
可以这么说,我有三个参赛者,想通过简单的矩阵乘法来测试他们的表现。参赛者是:
- Numpy,仅使用
dot 的功能。
- Python,通过共享对象调用 BLAS 功能。
- C++,通过共享对象调用 BLAS 功能。
场景
我实现了不同维度i的矩阵-矩阵乘法。 i 从 5 运行到 500,增量为 5,矩阵 m1 和 m2 设置如下:
m1 = numpy.random.rand(i,i).astype(numpy.float32)
m2 = numpy.random.rand(i,i).astype(numpy.float32)
1. Numpy
使用的代码看起来像这样:
tNumpy = timeit.Timer("numpy.dot(m1, m2)", "import numpy; from __main__ import m1, m2")
rNumpy.append((i, tNumpy.repeat(20, 1)))
2. Python,通过共享对象调用 BLAS
使用该函数,
_blaslib = ctypes.cdll.LoadLibrary("libblas.so")
def Mul(m1, m2, i, r):
no_trans = c_char("n")
n = c_int(i)
one = c_float(1.0)
zero = c_float(0.0)
_blaslib.sgemm_(byref(no_trans), byref(no_trans), byref(n), byref(n), byref(n),
byref(one), m1.ctypes.data_as(ctypes.c_void_p), byref(n),
m2.ctypes.data_as(ctypes.c_void_p), byref(n), byref(zero),
r.ctypes.data_as(ctypes.c_void_p), byref(n))
测试代码看起来像这样:
r = numpy.zeros((i,i), numpy.float32)
tBlas = timeit.Timer("Mul(m1, m2, i, r)", "import numpy; from __main__ import i, m1, m2, r, Mul")
rBlas.append((i, tBlas.repeat(20, 1)))
3. c++,通过共享对象调用 BLAS
现在,c++ 代码自然有点长,所以我将信息减少到最小值。
我加载该函数并
void* handle = dlopen("libblas.so", RTLD_LAZY);
void* Func = dlsym(handle, "sgemm_");
使用 gettimeofday 测量时间,如下所示:
gettimeofday(&start, NULL);
f(&no_trans, &no_trans, &dim, &dim, &dim, &one, A, &dim, B, &dim, &zero, Return, &dim);
gettimeofday(&end, NULL);
dTimes[j] = CalcTime(start, end);
其中 j 是运行 20 次的循环。 计算经过的时间
double CalcTime(timeval start, timeval end)
{
double factor = 1000000;
return (((double)end.tv_sec) * factor + ((double)end.tv_usec) - (((double)start.tv_sec) * factor + ((double)start.tv_usec))) / factor;
}
我用结果
结果如下图所示:
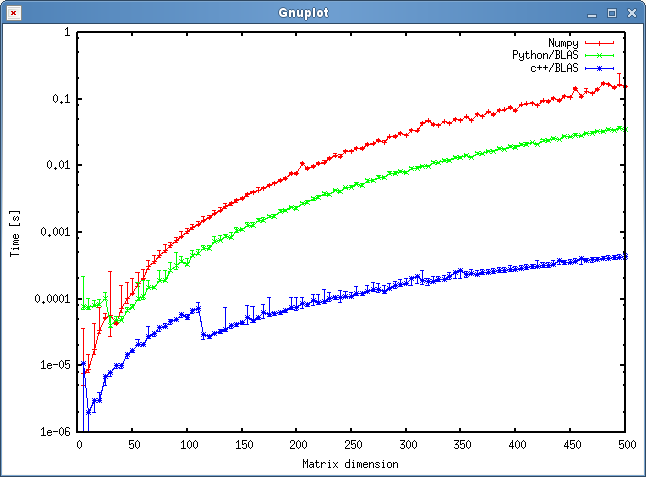
问题
- 你认为我的方法吗是公平的,还是有一些我可以避免的不必要的开销?
- 您是否期望结果会显示 c++ 和 python 方法之间存在如此巨大的差异?两者都使用共享对象进行计算。
- 由于我更愿意在我的程序中使用 python,那么在调用 BLAS 或 LAPACK 例程时我可以做些什么来提高性能?
下载
完整的基准测试可以在此处下载。 (JF Sebastian 使该链接成为可能^^)
I would like to write a program that makes extensive use of BLAS and LAPACK linear algebra functionalities. Since performance is an issue I did some benchmarking and would like know, if the approach I took is legitimate.
I have, so to speak, three contestants and want to test their performance with a simple matrix-matrix multiplication. The contestants are:
- Numpy, making use only of the functionality of
dot.
- Python, calling the BLAS functionalities through a shared object.
- C++, calling the BLAS functionalities through a shared object.
Scenario
I implemented a matrix-matrix multiplication for different dimensions i. i runs from 5 to 500 with an increment of 5 and the matricies m1 and m2 are set up like this:
m1 = numpy.random.rand(i,i).astype(numpy.float32)
m2 = numpy.random.rand(i,i).astype(numpy.float32)
1. Numpy
The code used looks like this:
tNumpy = timeit.Timer("numpy.dot(m1, m2)", "import numpy; from __main__ import m1, m2")
rNumpy.append((i, tNumpy.repeat(20, 1)))
2. Python, calling BLAS through a shared object
With the function
_blaslib = ctypes.cdll.LoadLibrary("libblas.so")
def Mul(m1, m2, i, r):
no_trans = c_char("n")
n = c_int(i)
one = c_float(1.0)
zero = c_float(0.0)
_blaslib.sgemm_(byref(no_trans), byref(no_trans), byref(n), byref(n), byref(n),
byref(one), m1.ctypes.data_as(ctypes.c_void_p), byref(n),
m2.ctypes.data_as(ctypes.c_void_p), byref(n), byref(zero),
r.ctypes.data_as(ctypes.c_void_p), byref(n))
the test code looks like this:
r = numpy.zeros((i,i), numpy.float32)
tBlas = timeit.Timer("Mul(m1, m2, i, r)", "import numpy; from __main__ import i, m1, m2, r, Mul")
rBlas.append((i, tBlas.repeat(20, 1)))
3. c++, calling BLAS through a shared object
Now the c++ code naturally is a little longer so I reduce the information to a minimum.
I load the function with
void* handle = dlopen("libblas.so", RTLD_LAZY);
void* Func = dlsym(handle, "sgemm_");
I measure the time with gettimeofday like this:
gettimeofday(&start, NULL);
f(&no_trans, &no_trans, &dim, &dim, &dim, &one, A, &dim, B, &dim, &zero, Return, &dim);
gettimeofday(&end, NULL);
dTimes[j] = CalcTime(start, end);
where j is a loop running 20 times. I calculate the time passed with
double CalcTime(timeval start, timeval end)
{
double factor = 1000000;
return (((double)end.tv_sec) * factor + ((double)end.tv_usec) - (((double)start.tv_sec) * factor + ((double)start.tv_usec))) / factor;
}
Results
The result is shown in the plot below:

Questions
- Do you think my approach is fair, or are there some unnecessary overheads I can avoid?
- Would you expect that the result would show such a huge discrepancy between the c++ and python approach? Both are using shared objects for their calculations.
- Since I would rather use python for my program, what could I do to increase the performance when calling BLAS or LAPACK routines?
Download
The complete benchmark can be downloaded here. (J.F. Sebastian made that link possible^^)



发布评论
评论(5)
更新(2014 年 7 月 30 日):
我在新的 HPC 上重新运行了基准测试。
硬件和软件堆栈都与原始答案中的设置发生了变化。
我将结果放入 Google 电子表格(还包含原始答案的结果)。
硬件
我们的 HPC 有两种不同的节点,一种采用 Intel Sandy Bridge CPU,另一种采用较新的 Ivy Bridge CPU:
Sandy(MKL、OpenBLAS、ATLAS):
Ivy(MKL、 OpenBLAS、ATLAS):
软件
两个节点的软件堆栈相同。使用OpenBLAS代替GotoBLAS2,并且还有一个设置为8个线程(硬编码)的多线程ATLAS BLAS。
点积基准
基准代码如下。不过,对于新机器,我还运行了矩阵大小 5000 和 8000 的基准测试。
下表包括原始答案的基准测试结果(重命名:MKL --> Nehalem MKL、Netlib Blas --> Nehalem Netlib BLAS 等)
单线程性能:
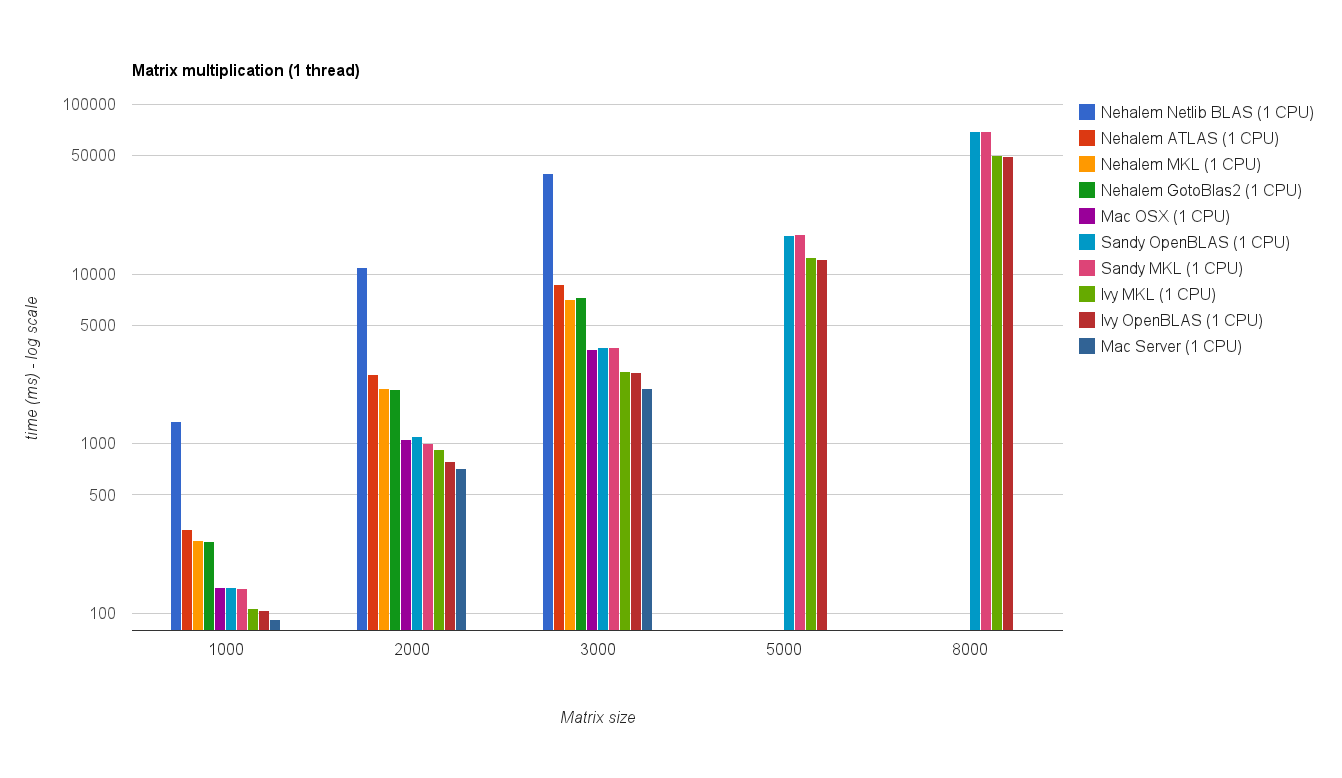
多线程性能(8 个线程):
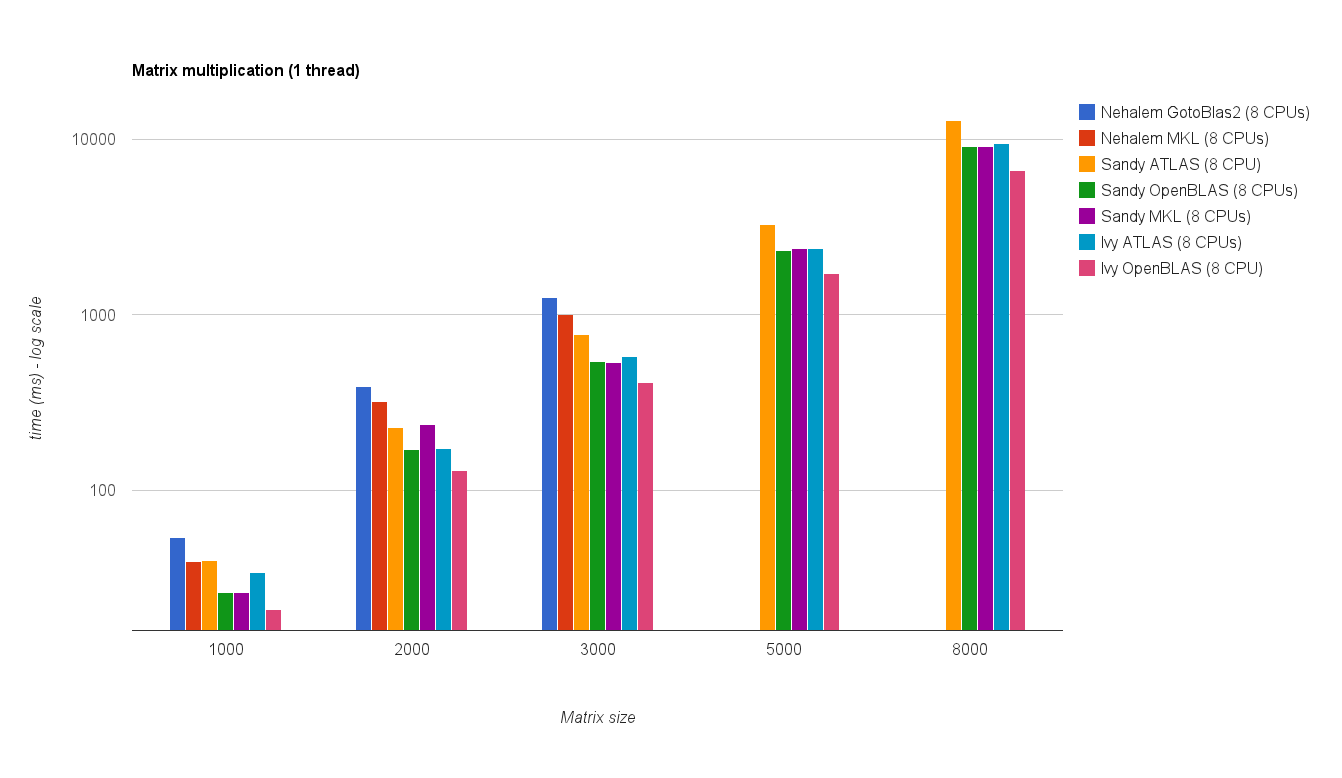
线程与矩阵大小 (Ivy Bridge MKL):
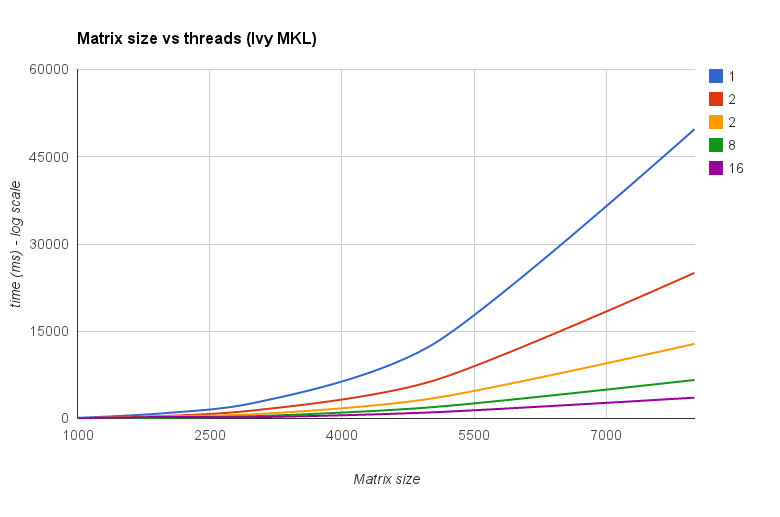
基准套件
单线程性能:
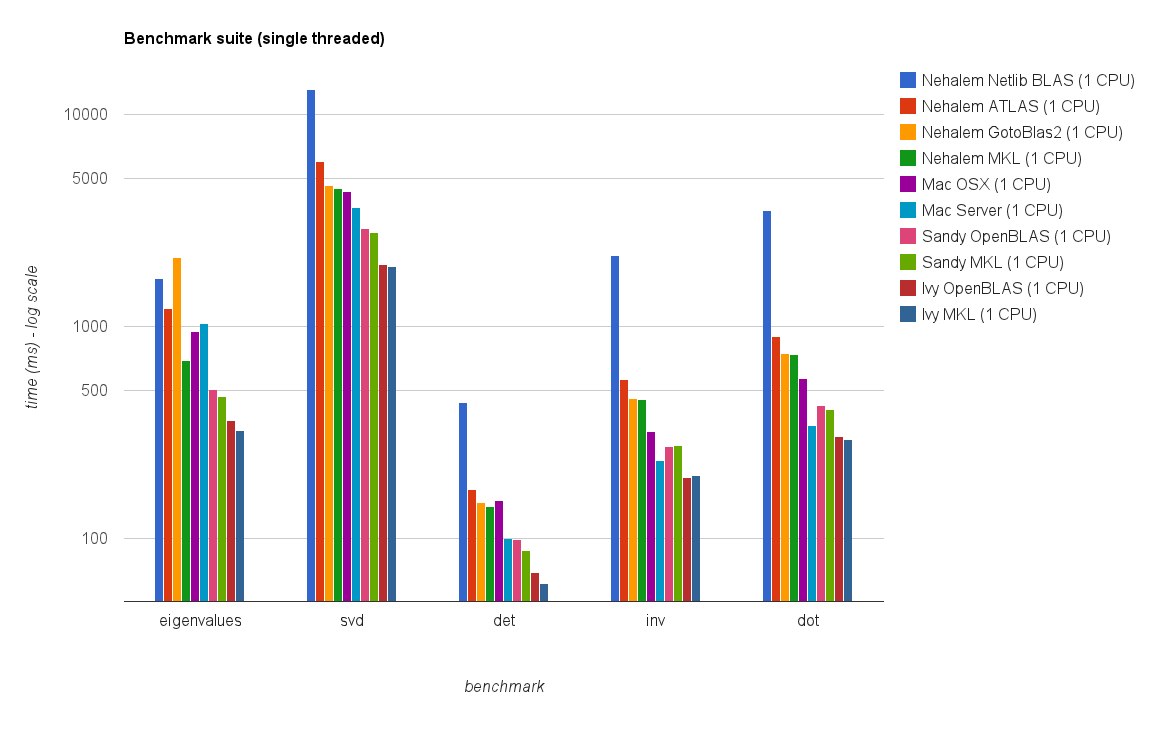
多线程(8 线程)性能:
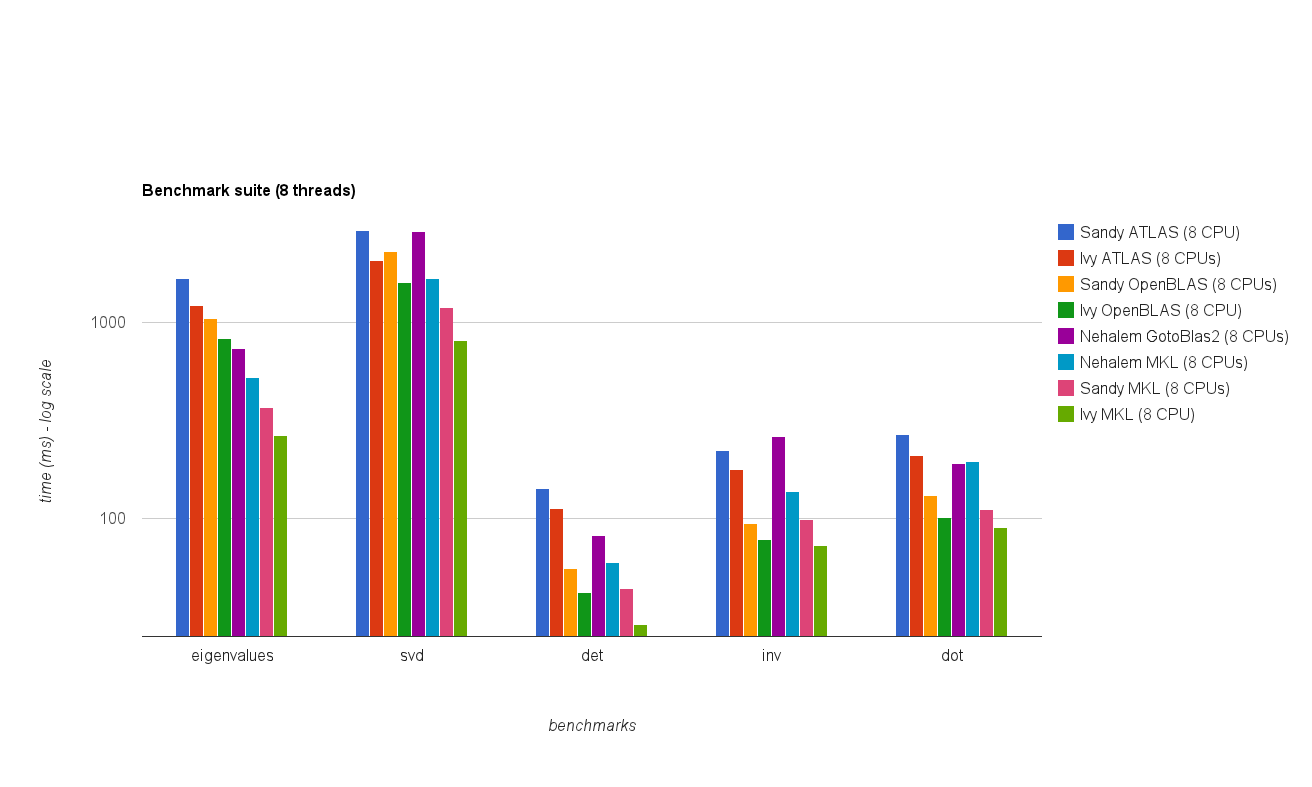
结论
新的基准测试结果与原始答案中的结果类似。除了特征值测试之外,OpenBLAS 和MKL 的性能处于同一水平。
特征值测试仅在单线程模式下的OpenBLAS上表现得相当好。
在多线程模式下性能较差。
“矩阵大小与线程图表”还显示,虽然 MKL 以及 OpenBLAS 通常可以很好地随内核/线程数量进行扩展,但它取决于矩阵的大小。对于小型矩阵,添加更多核心不会显着提高性能。
从 Sandy Bridge 到 Ivy Bridge 性能也提高了大约 30%,这可能是由于更高的时钟速率 (+ 0.8 Ghz) 和/或更好的架构。
原始答案(04.10.2011):
前段时间我必须优化一些使用 numpy 和 BLAS 用 python 编写的线性代数计算/算法,所以我对不同的 numpy/BLAS 配置进行了基准测试/测试。
具体来说,我测试了:
我确实运行了两个不同的基准测试:
以下是我的结果:
机器
Linux(MKL、ATLAS、No-MKL、GotoBlas2):
Mac Book Pro(加速框架):
Mac Server(加速框架):
点积基准
代码:
结果:
基准套件
代码:
有关基准测试套件的更多信息,请参阅此处< /a>.
结果:
安装
MKL 的安装包括安装完整的英特尔编译器套件非常简单。然而,由于一些错误/问题,使用 MKL 支持配置和编译 numpy 有点麻烦。
GotoBlas2 是一个小包,可以轻松编译为共享库。然而,由于 bug 你有在构建共享库后重新创建共享库,以便将其与 numpy 一起使用。
除此之外,由于某种原因,为多个目标平台构建它并不起作用。因此,我必须为每个我想要优化的 libgoto2.so 文件的平台创建一个 .so 文件。
如果您从 Ubuntu 的存储库安装 numpy,它将自动安装并配置 numpy 以使用 ATLAS。从源代码安装 ATLAS 可能需要一些时间,并且需要一些额外的步骤(fortran 等)。
如果您在具有 Fink 或 Mac Ports 的 Mac OS X 计算机上安装 numpy,它会将 numpy 配置为使用 ATLAS 或 Apple 的 Accelerate框架。
您可以通过在 numpy.core._dotblas 文件上运行 ldd 或调用 numpy.show_config() 进行检查。
结论
MKL 表现最佳,紧随其后的是 GotoBlas2。
在特征值测试中,GotoBlas2 的表现出奇地比预期差。不知道为什么会出现这种情况。
Apple 的 Accelerate Framework 性能非常好,尤其是在单线程模式下(与其他 BLAS 实现相比)。
GotoBlas2 和 MKL 都可以很好地适应线程数量。因此,如果您必须处理大矩阵,那么在多个线程上运行它会很有帮助。
无论如何,不要使用默认的 netlib blas 实现,因为它对于任何严肃的计算工作来说都太慢了。
在我们的集群上,我还安装了 AMD 的 ACML,性能与 MKL 和 GotoBlas2 类似。我没有任何数字。
我个人建议使用GotoBlas2,因为它更容易安装而且是免费的。
如果你想用 C++/C 编写代码,还可以查看 Eigen3 ,它应该是在某些案例中优于MKL/GotoBlas2,并且也很容易使用。
UPDATE (30.07.2014):
I re-run the the benchmark on our new HPC.
Both the hardware as well as the software stack changed from the setup in the original answer.
I put the results in a google spreadsheet (contains also the results from the original answer).
Hardware
Our HPC has two different nodes one with Intel Sandy Bridge CPUs and one with the newer Ivy Bridge CPUs:
Sandy (MKL, OpenBLAS, ATLAS):
Ivy (MKL, OpenBLAS, ATLAS):
Software
The software stack is for both nodes the sam. Instead of GotoBLAS2, OpenBLAS is used and there is also a multi-threaded ATLAS BLAS that is set to 8 threads (hardcoded).
Dot-Product Benchmark
Benchmark-code is the same as below. However for the new machines I also ran the benchmark for matrix sizes 5000 and 8000.
The table below includes the benchmark results from the original answer (renamed: MKL --> Nehalem MKL, Netlib Blas --> Nehalem Netlib BLAS, etc)
Single threaded performance:

Multi threaded performance (8 threads):

Threads vs Matrix size (Ivy Bridge MKL):

Benchmark Suite
Single threaded performance:

Multi threaded (8 threads) performance:

Conclusion
The new benchmark results are similar to the ones in the original answer. OpenBLAS and MKL perform on the same level, with the exception of Eigenvalue test.
The Eigenvalue test performs only reasonably well on OpenBLAS in single threaded mode.
In multi-threaded mode the performance is worse.
The "Matrix size vs threads chart" also show that although MKL as well as OpenBLAS generally scale well with number of cores/threads,it depends on the size of the matrix. For small matrices adding more cores won't improve performance very much.
There is also approximately 30% performance increase from Sandy Bridge to Ivy Bridge which might be either due to higher clock rate (+ 0.8 Ghz) and/or better architecture.
Original Answer (04.10.2011):
Some time ago I had to optimize some linear algebra calculations/algorithms which were written in python using numpy and BLAS so I benchmarked/tested different numpy/BLAS configurations.
Specifically I tested:
I did run two different benchmarks:
Here are my results:
Machines
Linux (MKL, ATLAS, No-MKL, GotoBlas2):
Mac Book Pro (Accelerate Framework):
Mac Server (Accelerate Framework):
Dot product benchmark
Code:
Results:
Benchmark Suite
Code:
For additional information about the benchmark suite see here.
Results:
Installation
Installation of MKL included installing the complete Intel Compiler Suite which is pretty straight forward. However because of some bugs/issues configuring and compiling numpy with MKL support was a bit of a hassle.
GotoBlas2 is a small package which can be easily compiled as a shared library. However because of a bug you have to re-create the shared library after building it in order to use it with numpy.
In addition to this building it for multiple target plattform didn't work for some reason. So I had to create an .so file for each platform for which i want to have an optimized libgoto2.so file.
If you install numpy from Ubuntu's repository it will automatically install and configure numpy to use ATLAS. Installing ATLAS from source can take some time and requires some additional steps (fortran, etc).
If you install numpy on a Mac OS X machine with Fink or Mac Ports it will either configure numpy to use ATLAS or Apple's Accelerate Framework.
You can check by either running ldd on the numpy.core._dotblas file or calling numpy.show_config().
Conclusions
MKL performs best closely followed by GotoBlas2.
In the eigenvalue test GotoBlas2 performs surprisingly worse than expected. Not sure why this is the case.
Apple's Accelerate Framework performs really good especially in single threaded mode (compared to the other BLAS implementations).
Both GotoBlas2 and MKL scale very well with number of threads. So if you have to deal with big matrices running it on multiple threads will help a lot.
In any case don't use the default netlib blas implementation because it is way too slow for any serious computational work.
On our cluster I also installed AMD's ACML and performance was similar to MKL and GotoBlas2. I don't have any numbers tough.
I personally would recommend to use GotoBlas2 because it's easier to install and it's free.
If you want to code in C++/C also check out Eigen3 which is supposed to outperform MKL/GotoBlas2 in some cases and is also pretty easy to use.
我已经运行了您的基准测试。在我的机器上 C++ 和 numpy 没有区别:
由于结果没有差异,这看起来很公平。
不。
确保 numpy 在您的系统上使用 BLAS/LAPACK 库的优化版本。
I've run your benchmark. There is no difference between C++ and numpy on my machine:
It seems fair due to there is no difference in results.
No.
Make sure that numpy uses optimized version of BLAS/LAPACK libraries on your system.
这是另一个基准测试(在 Linux 上,只需输入
make):http: //dl.dropbox.com/u/5453551/blas_call_benchmark.ziphttp://dl.dropbox.com/u/5453551/blas_call_benchmark.png
我愿意对于大型矩阵,Numpy、Ctypes 和 Fortran 之间的不同方法之间没有本质上的区别。 (Fortran 而不是 C++ --- 如果这很重要,那么您的基准测试可能已被破坏。)
C++ 中的
CalcTime函数似乎存在符号错误。... + ((double)start.tv_usec))应该改为... - ((double)start.tv_usec))。编辑:未能计算
CalcTime函数中的大括号 - 没关系。作为指导:如果您进行基准测试,请始终将所有代码发布到某处。在没有完整代码的情况下对基准进行评论,尤其是在令人惊讶的情况下,通常效率不高。
要找出 Numpy 链接到哪个 BLAS,请执行以下操作:
$ python Python 2.7.2+ (default, Aug 16 2011, 07:24:41) [GCC 4.6.1] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> import numpy.core._dotblas >>> numpy.core._dotblas.__file__ '/usr/lib/pymodules/python2.7/numpy/core/_dotblas.so' >>> $ ldd /usr/lib/pymodules/python2.7/numpy/core/_dotblas.so linux-vdso.so.1 => (0x00007fff5ebff000) libblas.so.3gf => /usr/lib/libblas.so.3gf (0x00007fbe618b3000) libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6 (0x00007fbe61514000)更新:如果您无法导入 numpy.core._dotblas,则您的 Numpy 正在使用 BLAS 的内部后备副本,速度较慢,不适合用于性能计算!
下面@Woltan 的回复表明,这是他/她在 Numpy 与 Ctypes+BLAS 中看到的差异的解释。
要解决此问题,您需要 ATLAS 或 MKL --- 检查以下说明: http://scipy.org/Installing_SciPy /Linux 大多数 Linux 发行版都附带 ATLAS,因此最好的选择是安装其
libatlas-dev软件包(名称可能有所不同)。Here's another benchmark (on Linux, just type
make): http://dl.dropbox.com/u/5453551/blas_call_benchmark.ziphttp://dl.dropbox.com/u/5453551/blas_call_benchmark.png
I do not see essentially any difference between the different methods for large matrices, between Numpy, Ctypes and Fortran. (Fortran instead of C++ --- and if this matters, your benchmark is probably broken.)
Your
CalcTimefunction in C++ seems to have a sign error.... + ((double)start.tv_usec))should be instead... - ((double)start.tv_usec)).EDIT: failed to count the braces in the
CalcTimefunction -- it's OK.As a guideline: if you do a benchmark, please always post all the code somewhere. Commenting on benchmarks, especially when surprising, without having the full code is usually not productive.
To find out which BLAS Numpy is linked against, do:
$ python Python 2.7.2+ (default, Aug 16 2011, 07:24:41) [GCC 4.6.1] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> import numpy.core._dotblas >>> numpy.core._dotblas.__file__ '/usr/lib/pymodules/python2.7/numpy/core/_dotblas.so' >>> $ ldd /usr/lib/pymodules/python2.7/numpy/core/_dotblas.so linux-vdso.so.1 => (0x00007fff5ebff000) libblas.so.3gf => /usr/lib/libblas.so.3gf (0x00007fbe618b3000) libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6 (0x00007fbe61514000)UPDATE: If you can't import numpy.core._dotblas, your Numpy is using its internal fallback copy of BLAS, which is slower, and not meant to be used in performance computing!
The reply from @Woltan below indicates that this is the explanation for the difference he/she sees in Numpy vs. Ctypes+BLAS.
To fix the situation, you need either ATLAS or MKL --- check these instructions: http://scipy.org/Installing_SciPy/Linux Most Linux distributions ship with ATLAS, so the best option is to install their
libatlas-devpackage (name may vary).鉴于您的分析所表现出的严谨性,迄今为止的结果令我感到惊讶。我将其作为“答案”,但只是因为它对于评论来说太长并且确实提供了可能性(尽管我希望您已经考虑过它)。
我本以为 numpy/python 方法不会为具有合理复杂性的矩阵增加太多开销,因为随着复杂性的增加,python 参与的比例应该很小。我对图表右侧的结果更感兴趣,但显示的数量级差异会令人不安。
我想知道您是否正在使用 numpy 可以利用的最佳算法。来自 Linux 的编译指南:
“构建 FFTW (3.1.2):
SciPy 版本 >= 0.7 和 Numpy >= 1.2:
由于许可证、配置和维护问题,SciPy >= 0.7 和 NumPy >= 1.2 版本中删除了对 FFTW 的支持。现在改为使用 fftpack 的内置版本。
如果您的分析需要的话,有几种方法可以利用 FFTW 的速度。
降级到包含支持的 Numpy/Scipy 版本。
安装或创建您自己的 FFTW 包装器。请参阅 http://developer.berlios.de/projects/pyfftw/ 作为未经认可的例如。”
您是否使用 mkl 编译了 numpy?(http://www.scipy.org/Installing_SciPy/Linux#head-7ce43956a69ec51c6f2cedd894a4715d5bfff974(尽管有url),关键部分是:
如果你在Windows上,你可以获得一个使用 mkl 编译二进制文件(并且还获得 pyfftw 和许多其他相关算法)位于: http://www.lfd.uci.edu/~gohlke/pythonlibs/,其中感谢加州大学欧文分校荧光动力学实验室的 Christoph Gohlke。
警告,无论哪种情况,都有许多许可问题等需要注意,但英特尔页面对此进行了解释。再说一次,我想你已经考虑过这一点,但是如果你满足许可要求(这在 Linux 上很容易做到),相对于使用简单的自动构建,这将大大加快 numpy 部分的速度,甚至不需要 FFTW。我有兴趣关注此主题并看看其他人的想法。无论如何,非常严谨,问题也很好。感谢您发布它。
Given the rigor you've shown with your analysis, I'm surprised by the results thus far. I put this as an 'answer' but only because it's too long for a comment and does provide a possibility (though I expect you've considered it).
I would've thought the numpy/python approach wouldn't add much overhead for a matrix of reasonable complexity, since as the complexity increases, the proportion that python participates in should be small. I'm more interested in the results on the right hand side of the graph, but orders of magnitude discrepancy shown there would be disturbing.
I wonder if you're using the best algorithms that numpy can leverage. From the compilation guide for linux:
"Build FFTW (3.1.2):
SciPy Versions >= 0.7 and Numpy >= 1.2:
Because of license, configuration, and maintenance issues support for FFTW was removed in versions of SciPy >= 0.7 and NumPy >= 1.2. Instead now uses a built-in version of fftpack.
There are a couple ways to take advantage of the speed of FFTW if necessary for your analysis.
Downgrade to a Numpy/Scipy version that includes support.
Install or create your own wrapper of FFTW. See http://developer.berlios.de/projects/pyfftw/ as an un-endorsed example."
Did you compile numpy with mkl? (http://software.intel.com/en-us/articles/intel-mkl/). If you're running on linux, the instructions for compiling numpy with mkl are here: http://www.scipy.org/Installing_SciPy/Linux#head-7ce43956a69ec51c6f2cedd894a4715d5bfff974 (in spite of url). The key part is:
If you're on windows, you can obtain a compiled binary with mkl, (and also obtain pyfftw, and many other related algorithms) at: http://www.lfd.uci.edu/~gohlke/pythonlibs/, with a debt of gratitude to Christoph Gohlke at the Laboratory for Fluorescence Dynamics, UC Irvine.
Caveat, in either case, there are many licensing issues and so on to be aware of, but the intel page explains those. Again, I imagine you've considered this, but if you meet the licensing requirements (which on linux is very easy to do), this would speed up the numpy part a great deal relative to using a simple automatic build, without even FFTW. I'll be interested to follow this thread and see what others think. Regardless, excellent rigor and excellent question. Thanks for posting it.
让我为一个有点奇怪的发现做出贡献
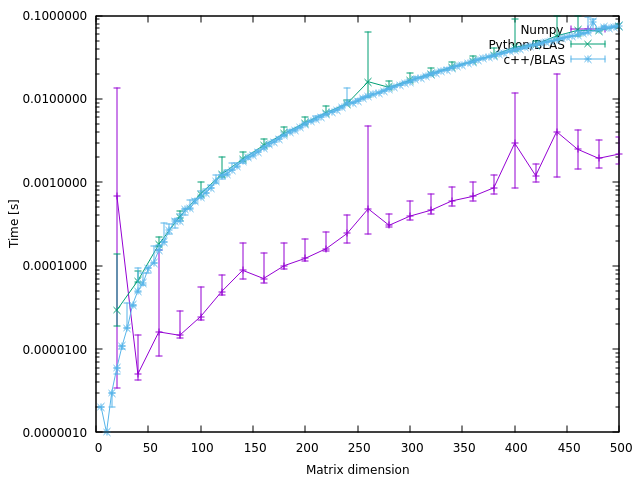
我的
numpy链接到mkl,如 numpy.show_config() 所示。我不知道使用了什么样的libblas.soC++/BLAS。我希望有人能告诉我一个方法来解决这个问题。我认为结果很大程度上取决于所使用的库。我无法孤立 C++/BLAS 的效率。
Let me contribute to a somewhat weird finding

My
numpyis linked tomkl, as given by numpy.show_config(). I have no idea what kind oflibblas.soC++/BLAS was used. I hope someone can tell me a way to figure it out.I think the results strongly depend on the library was used. I cannot isolate the efficiency of C++/BLAS.