基于多边形的寻路
我已经用 Java 实现了一个基于网格的基本 A* 探路者。我想制作一个基于导航网格/多边形的探路器,但我遇到的问题是:
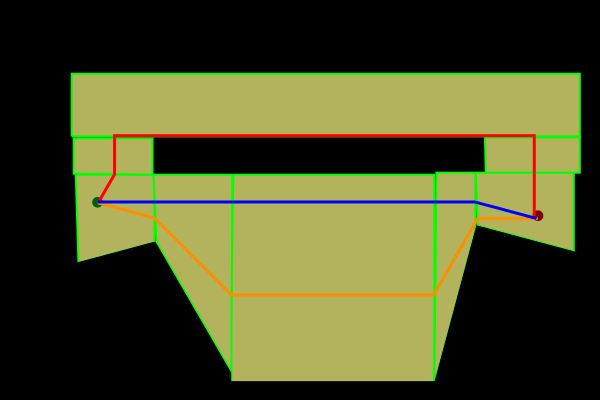
如果我找到了橙色路线,那么我可以使用类似 漏斗算法来拉直它以获得所需的路线(蓝色)。然而,如果程序计算每条路线(红色和橙色)的成本,那么它会说红色路线是最便宜的路线。如何对我的 A* 算法进行编程和/或创建我的网格体以避免这种情况发生。
I have implemented a basic grid based A* pathfindinder in Java. I would like to make a navigational mesh/polygon based pathfinder, but the problem I have is this:

If I found the orange route then I could use something like a funnel algorithm to straighten it to get the desired route (blue). However, if the program calculates the cost of each of the routes, red and orange, then it will say the red one is the cheaper one. How do I program my A* algorithm and/or create my meshes so that this doesn't happen.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
抱歉,我无法直接帮助您解决问题,但我们将基于多边形的探路器移植到 haxe,它可以编译为 java(到目前为止仅尝试过 swing,但可能很快会尝试 slick2d),并且可以根据一些研究将其集成到 Java 项目中。它名为 hxDaedalus,位于 github 上,可能是一个有趣的参考点。
Sorry I can't help with your question directly, but we ported a polygon based pathfinder to haxe and it can compile to java ( only tried with swing so far but might try slick2d soon ) and could be integrated into a Java project given some research. It's called hxDaedalus and is on github and might be an interesting point of reference.
计算几何:算法与应用中的第15章描述并解决了这个问题:自由空间可以可以用梯形地图来描述,但是使用地图找到的路径不一定是最短的。推荐的表示(也在 LaValle 的 规划算法(第 6.2.4 节) 中讨论过)是所谓的可见性图,它具有连接障碍物顶点的边。
伪代码和图表可从本书主页和 Google 预览也包含本章的部分内容。
Chapter 15 in Computational Geometry: Algorithms and Applications describes and solves exactly this problem: the free space can be described by a trapezoidal map, but paths found using the map aren't necessarily the shortest. The recommended representation (also discussed in LaValle's Planning Algorithms (Section 6.2.4)) is a so-called visibility graph, which has edges that connect vertices of the obstacles.
Pseudo-code and figures are available from the book homepage and the Google preview also contains parts of the chapter.