在屏幕上绘制 n 个 GPS 坐标，而不是*不*任何地图

Question

假设我在位置 M（纬度，经度），并且我还有 3 个 GPS 坐标 A（纬度，经度），B（纬度，经度）和 C（纬度，经度），它们都在 M 周围 500 米半径范围内

注意：我想在屏幕上将它们相对于彼此绘制，但不与任何其他地图或其他任何东西以及 GPS 数量M 周围的点可能会增加或减少但始终位于 M 周围 500 米半径内。M

将位于屏幕中心。 ScreeWidth=320，ScreenHeight=400

我有以下信息

M =  31.484083, 74.392708,

A =  31.483552, 74.392386 and distance from M is 66.42 Meters approximately
B =  31.483534, 74.392532 and distance from M is 63.23 Meters approximately
C =  31.483421, 74.392434 and distance from M is 78.00 Meters approximately

M 将在屏幕的 WIDTH/2 和 HEIGHT/2 处绘制

A、B 和 C 需要一个转换函数，该函数将返回 x 和 y（以像素为单位），并尊重 M 和

屏幕宽度和高度，请记住这些点始终位于 M 周围 500 米半径内。

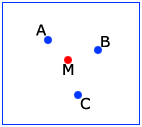
这样我就可以绘制这些点，如下图所示。

这是图像：

https://picasaweb.google.com/lh/photo/J7PE6RuSqu7Pv9xv9D2PgQ?feat= directlink

我只需要 x 和 y 的转换函数，我知道怎么做将它们绘制在屏幕上

Answer 1

好吧，您需要实现一种将纬度/经度映射到像素，并将像素映射到纬度经度的方法...或者确定距参考点 M 的距离/方位角的方法，然后将该距离/方位角映射到像素值。

如果您希望通过纬度/经度进行引用，请使用每像素纬度的一定度数和每像素经度的一定度数的线性像素图。我建议您访问 google 地球，检查您感兴趣的区域 500 米的纬度和经度差异。世界上所有点的纬度设置为每度 60 海里，我很确定经度大约是每度 60*cos(lat) 海里（近似值，谷歌搜索一下）。

如果您希望通过距离进行参考，我建议使用球形地球近似，并使用半正弦建立一种方法来确定跨越大球体的距离。如果您使用 matlab，找到此类示例的最佳位置是文件交换中的 google 或 mathworks.com。

当你有办法将经纬度或距离/纬度映射到像素值后......剩下的就是绘图了。

祝你好运

下面是名为 vreckon 和 geodistance 的代码，如果你想在 java 中实现，你可以自己解析它 - 我自己已经做了 vreckon 所以我会给你工作 vreckon java，如果你想做 geodistance （检查之间的距离两个经纬度点）你需要自己做。

VRECKON 的 JAVA 代码 ::::::

hvDistance 是距您的经纬度点的水平距离，latitudeOrigin 和 longitudeOrigin 是您的纬度/经度位置，方位角是距您的原点的方向。

输出将是新的纬度和经度点。如果您想在 java 中实现，您应该能够通过 matlab 代码并对下面的地理距离执行相同的操作。这正是使您达到 WGS84 标准精度的东西。享受

private void vreckon(){
    double rng = hvDistance; 

    double m = 6;
    double a = 6378137.0;
    double f = 1/298.257223563;
    double b = a*(1-f);
    double lat0 = deg2rad(latitudeOrigin);
    double lon0 = deg2rad(longitudeOrigin);
    double az = deg2rad(azimuth);

    double axa = a*a;
    double bxb = b*b;

    double tan_U1 = (1-f)*Math.sin(lat0)/Math.cos(lat0);

    double U1 = Math.atan(tan_U1);
    double cos_alfa1 = Math.cos(az);
    double sig1 = Math.atan2(tan_U1, cos_alfa1);

    double cos_U1 = Math.cos(U1);
    double sin_alfa1 = Math.sin(az);

    double sin_alfa = cos_U1*sin_alfa1;

    double cos2_alfa = (1-sin_alfa)*(1+sin_alfa);
    double uxu = cos2_alfa*(axa-bxb)/bxb;

    double A = 1+uxu/16384*(4096+uxu*(-768+uxu*(320-175*uxu)));
    double B = uxu/1024*(256+uxu*(-128+uxu*(74-47*uxu)));

    double sig = rng/(b*A);

    double change = 1;

    double twosig_m;
    double cos_twosig_m;
    double cos2_twosig_m;
    double dsig;
    double sigold;

    while(Math.abs(change) > 1e-9){
        twosig_m = 2*sig1+sig;
        cos_twosig_m = Math.cos(twosig_m);
        cos2_twosig_m = cos_twosig_m*cos_twosig_m;
        dsig = B*Math.sin(sig)*(cos_twosig_m+1/4*B*(Math.cos(sig)*(-1+2.*cos2_twosig_m)-1/6*B*cos_twosig_m*(-3+4*(Math.sin(sig)*Math.sin(sig)))*(-3+4*cos2_twosig_m)));
        sigold = sig;
        sig = rng/(b*A)+dsig;
        change = sig-sigold;
    }

    twosig_m = 2*sig1+sig;

    cos_twosig_m = Math.cos(twosig_m);
    cos2_twosig_m = cos_twosig_m*cos_twosig_m;
    double sin_U1 = Math.sin(U1);

    double cos_sig = Math.cos(sig);
    double sin_sig = Math.sin(sig);
    double sin2_alfa = sin_alfa*sin_alfa;

    double latOut = Math.atan2(sin_U1*cos_sig+cos_U1*sin_sig*cos_alfa1,(1-f)*Math.sqrt(sin2_alfa+(sin_U1*sin_sig-cos_U1*cos_sig*cos_alfa1)*(sin_U1*sin_sig-cos_U1*cos_sig*cos_alfa1)));

    double lambda = Math.atan2(sin_sig*sin_alfa1,cos_U1*cos_sig-sin_U1*sin_sig*cos_alfa1);
    double C = f/16*cos2_alfa*(4+f*(4-3*cos2_alfa));
    double L = lambda-(1-C)*f*sin_alfa*(sig+C*sin_sig*(cos_twosig_m+C*cos_sig*(-1+2*cos2_twosig_m)));

    double lonOut = L+lon0;

    latOut = rad2deg(latOut);
    lonOut = rad2deg(lonOut);

    reckonedLatitude = latOut;
    reckonedLongitude = lonOut;
}

用于地理距离的 MATLAB 代码 :::::

function [r az] = geodistance(lat1,lon1,lat2,lon2,ellip,earthR)
%GEODISTANCE: Calculates the distance in meters between two points on earth surface.
%
% Usage:  r = geodistance(lat1,lon1,lat2,lon2, ellipsoid ) ;
%
%     Coordinates values should be specified in decimal degrees.
%     Method can be an integer between 1 and 23, default is m = 6.
%         Methods 1 and 2 are based on spherical trigonometry and a
%         spheroidal model for the earth, respectively.
%     Methods 3 to 24 use Vincenty's formulae, based on ellipsoid
%         parameters.
%         Here it follows the correspondence between m and thge type of
%         ellipsoid:
%
%         m =  3 -> ANS ,        m =  4 -> GRS80,    m = 5 -> WGS72,
%         m =  6 -> WGS84,       m =  7 -> NSWC-9Z2,
%         m =  8 -> Clarke 1866, m =  9 -> Clarke 1880,
%         m = 10 -> Airy 1830,
%         m = 11 -> Bessel 1841 (Ethiopia,Indonesia,Japan,Korea),
%         m = 12 -> Bessel 1841 (Namibia),
%         m = 13 -> Sabah and Sarawak (Everest,Brunei,E.Malaysia),
%         m = 14 -> India 1830, m = 15 -> India 1956,
%         m = 16 -> W. Malaysia and Singapore 1948,
%         m = 17 -> W. Malaysia 1969,
%         m = 18 -> Helmert 1906, m = 19 -> Helmert 1960,
%         m = 20 -> Hayford International 1924,
%         m = 21 -> Hough 1960, m = 22 -> Krassovsky 1940,
%         m = 23 -> Modified Fischer 1960,
%         m = 24 -> South American 1969.
%
%     Important notes:
%
%    1)South latitudes are negative.
%    2)East longitudes are positive.
%    3)Great circle distance is the shortest distance between two points
%          on a sphere. This coincides with the circumference of a circle which
%          passes through both points and the centre of the sphere.
%    4)Geodesic distance is the shortest distance between two points on a spheroid.
%    5)Normal section distance is formed by a plane on a spheroid containing a
%          point at one end of the line and the normal of the point at the other end.
%          For all practical purposes, the difference between a normal section and a
%          geodesic distance is insignificant.
%    6)The method m=2 assumes a spheroidal model for the earth with an average
%          radius of 6364.963 km. It has been derived for use within Australia.
%          The formula is estimated to have an accuracy of about 200 metres over 50 km,
%          but may deteriorate with longer distances.
%          However, it is not symmetric when the points are exchanged.
%***************************************************************************************
% Based loosely from code from [email protected]
% Vastly modified and improved.
% By J. Sullivan 12/2010
%***************************************************************************************

%% Defensive Programming

error(nargchk(4,6,nargin));

if any([isempty(lat1) isempty(lon1) isempty(lat2) isempty(lon2)]);
    error('One or more input arguments are empty.')
end
%% Farm out to GPU, if possible
if any([numel(lat1) numel(lat2) numel(lon1) numel(lon2)] >  250000) ...
        && ~any([numel(lat1) numel(lat2) numel(lon1) numel(lon2)] > 6000000)
    [lat1 lat2 lon1 lon2] = makeIntoGPUArrays(lat1,lat2,lon1,lon2);
end
%% Prepare the Data
r = [ ];
lambda1 = lon1*pi/180;
phi1 = lat1*pi/180;
lambda2 = lon2*pi/180;
phi2 = lat2*pi/180;
isEast = lon1 < lon2;
L = lambda2 - lambda1;
%% Load Earth Ellipsoid Models
alla = [earthRadius 0 6378160 6378137.0 6378135 6378137.0 6378145 6378206.4 6378249.145,...
    6377563.396 6377397.155 6377483.865,...
    6377298.556 6377276.345 6377301.243 6377304.063 6377295.664 6378200 6378270 6378388  6378270 6378245,...
    6378155 6378160];

allf = [0 0  1/298.25 1/298.257222101 1/298.26 1/298.257223563 1/298.25 1/294.9786982 1/293.465,...
    1/299.3249646 1/299.1528128,...
    1/299.1528128 1/300.8017 1/300.8017 1/300.8017 1/300.8017 1/300.8017 1/298.3 1/297 1/297 1/297,...
    1/298.3 1/298.3 1/298.25];
%% Choose Ellipsoid
if nargin > 4 && length(ellip) == 2;
    m = inf;
    a = ellip(1);
    b = a*cos(ellip(2));
    f = (a-b)/a;
elseif nargin < 5
    m = 6;
    a = alla(6);
    f = allf(6);
    b = a*(1-f);
elseif length(ellip) == 1
    m = ellip;
    a = alla(ellip);
    f = allf(ellip);
    b = a*(1-f);
end
samePoint = gather(abs( lambda1 - lambda2 ) < eps) & gather(abs( phi1 - phi2 ) < eps);
%% Sheperical Earth
if m == 1 % Great Circle Distance, based on spherical trigonometry
    clear lat1 lat2 lon1 lon2
    if nargin < 6; earthR = a; end
    tmp = sin(phi1).*sin(phi2)+cos(phi1).*cos(phi2).*cos(lambda2-lambda1);
    tmp(tmp > 1) = 1;
    r = earthR.*acos(tmp);
    r = gather(abs(r));
    if nargout > 1
        az = atan2(cos(phi2).*sin(lambda2-lambda1),cos(phi1).*sin(phi2)...
            -sin(phi1).*cos(phi2).*cos(lambda2-lambda1));
        % Azimuths are undefined at the poles, so we choose a convention: zero at
        % the north pole and pi at the south pole.
        az(phi1 <= -pi/2) = 0;
        az(phi2 >=  pi/2) = 0;
        az(phi2 <= -pi/2) = pi;
        az(phi1 >=  pi/2) = pi;
        az = gather(rad2deg(az));
    end

elseif m == 2 % Spheroidal model for the earth
    % Azimuth Calculations for this model are NOT consistant with a
    % spheriod.

    term1 = 111.08956*( lat1 - lat2 + 0.000001 );
    term2 = cos( phi1  + ( (phi2 - phi1)/2 ) );
    term3 = ( lon2 - lon1 + 0.000001 )/( lat2 - lat1 + 0.000001 );
    r = 1000*abs( term1/cos( atan( term2*term3 ) ) );
    if nargout > 1
        az = atan2(cos(phi2).*sin(lambda2-lambda1),cos(phi1).*sin(phi2)...
            -sin(phi1).*cos(phi2).*cos(lambda2-lambda1));
        % Azimuths are undefined at the poles, so we choose a convention: zero at
        % the north pole and pi at the south pole.
        az(phi1 <= -pi/2) = 0;
        az(phi2 >=  pi/2) = 0;
        az(phi2 <= -pi/2) = pi;
        az(phi1 >=  pi/2) = pi;
        az = rad2deg(az);
    end

else
    %% Apply Vincenty's formulae
    clear lambda1 lambda2 lat1 lat2 lon1 lon2

    axa = a^2;
    bxb = b^2;

    U1 = atan( ( 1 - f )*tan( phi1 ) );
    U2 = atan( ( 1 - f )*tan( phi2 ) );

    clear phi1 phi2

    lambda     =  L;
    lambda_old = sqrt(-1);
    ntrials = 0;

    while gather(any(any( abs( lambda - lambda_old ) > 1e-9 )))

        ntrials = ntrials + 1;

        lambda_old = lambda;
        sin_sigma = sqrt( ( cos(U2).*sin(lambda) ).^2 + ( cos(U1).*sin(U2) - sin(U1).*cos(U2).*cos(lambda) ).^2 );
        cos_sigma = sin( U1 ).*sin( U2 ) + cos( U1 ).*cos( U2 ).*cos( lambda );
        sigma = atan2( sin_sigma,cos_sigma );
        sin_alpha = cos( U1 ).*cos( U2 ).*sin( lambda )./sin_sigma;
        cos2_alpha = 1 - sin_alpha.^2;
        cos_2sigmam = cos_sigma - 2.*sin( U1 ).*sin( U2 )./cos2_alpha;

        C = (f/16).*cos2_alpha.*( 4 + f.*( 4 - 3.*cos2_alpha ) );

        lambda  = L + ( 1 - C ).*f.*sin_alpha.*( sigma + C.*sin_sigma.*( ...
            cos_2sigmam + C.*cos_sigma.*( -1 + 2*( cos_2sigmam ).^2 ) ) );

        if ntrials > 1000
            disp('Convergence failure...')
            return
        end
    end
    clear C sin_alpha lambda_old L
    %% Get Distance After Convergence acheived
    uxu = cos2_alpha.*(axa - bxb)./bxb;
    clear cos2_alpha bxb axa
    A = 1 + (uxu/16384).*(4096 + uxu.*(-768 + uxu.*(320 - 175.*uxu)));
    B = (uxu./1024).*(256 + uxu.*(-128 + uxu.*(74 - 47.*uxu)));
    clear uxu
    delta_sigma = B.*sin_sigma.*(cos_2sigmam + (B/4).*(cos_sigma.*...
        (-1 + 2.*cos_2sigmam.^2) -(B/6).*cos_2sigmam.*(-3 + 4.*sin_sigma.^2)...
        .*(-3 + 4.*cos_2sigmam.^2)));
    clear sin_sigma cos_sigma cos_2sigmam B
    delta_sigma(isnan(delta_sigma)) = 0;
    r = gather(b.*A.*(sigma - delta_sigma));
    clear sigma A delta_sigma
    %% Same Point Check
    r(samePoint) = 0;
    %% Calculate Azimuth if needed
    if nargout >= 2
        lambda(gather(isnan(lambda)) & gather(isEast)) = pi/2;
        lambda(gather(isnan(lambda)) & ~gather(isEast)) = -pi/2;
        az = rad2deg(atan2(cos(U2).*sin(lambda),cos(U1).*sin(U2)-sin(U1).*cos(U2).*cos(lambda)));
        clear U1 U2 lambda
        az = gather(zero22pi(az));
        az(samePoint) = 0;
    end
end

% clearvars -except az r

Answer 2

好吧，最后我设法编写了一个转换函数，它对我有用并且工作正常，因为我在不同位置进行了测试，并且参考中心点（M），所有其他点都以完美的比例显示。

public static POINT XY(double centerLatitude, double centerLongitude, double Latitude, double Longitude, double MetersPerPixel) {
    double rto = 1/MetersPerPixel;
    double dLAT = ((centerLatitude - Latitude)/ 0.00001) * rto;
    double dLNG = -1 * ((centerLongitude - Longitude) / 0.00001) * rto;
    int y = (int)Math.round(dLAT);
    int x = (int)Math.round(dLNG);
    POINT crd = new POINT(x, y );
    return crd;
}