我有一个结构良好的树,它代表一个数学表达式。例如,给定字符串:"1+2-3*4/5",它会被解析为:
subtract(add(1,2),divide(multiply(3,4),5))
表示为这棵树:

我想要做的是尽可能地减少这棵树。在上面的例子中,这非常简单,因为所有数字都是常量。然而,一旦我允许未知数(用 $ 后跟标识符表示),事情就开始变得更加棘手:
"3*$a/$a" 变成 split(multiply(3,$a), $a)
这应该简化为 3,因为 $a 项应该相互抵消。问题是,“我如何以通用的方式认识到这一点?”我如何识别 min(3, sin($x)) 始终为 sin($x)?如何识别 sqrt(pow($a, 2)) 是 abs($a)?我如何识别 nthroot(pow(42, $a), $a)(42 的第 a 根到第 a功率)是42?
我意识到这个问题相当广泛,但我已经为此绞尽脑汁有一段时间了,但还没有提出任何足够令人满意的答案。
I have a well-formed tree that represents a mathematical expression. For example, given the string: "1+2-3*4/5", this gets parsed into:
subtract(add(1,2),divide(multiply(3,4),5))
Which is expressed as this tree:
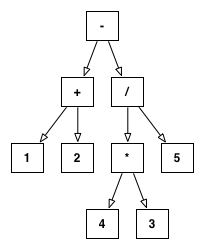
What I'd like to be able to do is take this tree and reduce it as much as possible. In the case above, this is pretty simple, because all of the numbers are constants. However, things start to get trickier once I allow for unknowns (denoted with a $ followed by an identifier):
"3*$a/$a" becomes divide(multiply(3,$a), $a)
This should simplify to 3, since the $a terms should cancel each other out. The question is, "how do I go about recognizing this in a generic manner?" How do I recognize that min(3, sin($x)) is always going to be sin($x)? How do I recognize that sqrt(pow($a, 2)) is abs($a)? How do I recognize that nthroot(pow(42, $a), $a) (the ath root of 42 to the ath power) is 42?
I realize this question is pretty broad, but I've been beating my head against this for a while and haven't come up with anything satisfactory enough.




发布评论
评论(6)
您可能想要实现术语重写系统。关于基础数学,请查看WikiPedia。
术语重写模块的结构
由于我最近实现了一个解决方案...
首先,准备一个类 CExpression,它对表达式的结构进行建模。
实现
CRule,其中包含模式和替换。使用特殊符号作为模式变量,需要在模式匹配时进行绑定,并在替换表达式中进行替换。然后,实现一个类
CRule。它的主要方法applyRule(CExpression, CRule)尝试将规则与表达式的任何适用的子表达式进行匹配。如果匹配,则返回结果。最后,实现一个类
CRuleSet,它只是一组 CRule 对象。主要方法reduce(CExpression)应用规则集,只要不能应用更多规则,然后返回简化的表达式。此外,您还需要一个类
CBindingEnvironment,它将已匹配的符号映射到匹配的值。尝试将表达式重写为正常形式
不要忘记,这种方法在一定程度上有效,但可能不完整。这是因为以下所有规则都执行局部术语重写。
为了使这种本地重写逻辑更强大,应该尝试将表达式转换为我称之为范式的东西。这是我的方法:
如果某个术语包含文字值,请尝试将该术语尽可能移到右侧。
最终,这个文字值可能出现在最右边,并且可以作为完整文字表达式的一部分进行计算。
何时计算完全文字表达式
一个有趣的问题是何时计算完全文字表达式。假设你有一个表达式
,它会减少到
现在假设 x 被 3 替换。这会产生类似的结果
,因此急切求值返回一个稍微不正确的值。
另一方面,如果保留 ( 1 / 3 ) 并首先将 x 替换为 3,则
重写规则将给出
因此,稍后评估完全文字表达式可能会很有用。
重写规则示例
以下是我的规则在应用程序中的显示方式: _1、_2、... 符号匹配任何子表达式:
或更复杂一些
某些特殊符号仅匹配特殊子表达式。例如 _Literal1, _Literal2, ... 仅匹配文字值:
此规则将非文字表达式移至左侧:
任何以“_”开头的名称都是模式变量。当系统匹配规则时,它会保留一堆已匹配符号的分配。
最后,不要忘记规则可能会产生非终止的替换序列。
因此,在减少表达式的同时,使过程记住之前已经到达了哪些中间表达式。
在我的实现中,我不直接保存中间表达式。我保留中间表达式的 MD5() 哈希数组。
一组规则作为起点
这是一组开始的规则:
使规则成为一流表达式
有趣的一点:由于上述规则是特殊表达式,因此通过表达式解析器正确评估,用户甚至可以添加新规则,从而增强应用程序的重写能力。
解析表达式(或更一般:语言)
对于 Cocoa/OBjC 应用程序,Dave DeLong 的 DDMathParser 是语法分析数学表达式的完美选择。
对于其他语言,我们的老朋友Lex & Yacc 或较新的 GNU Bison 可能会有所帮助。
更年轻,并且拥有大量可供使用的语法文件,ANTLR 是一个基于 Java 的现代解析器生成器。除了纯粹的命令行使用之外,ANTLRWorks 还提供了GUI 前端构建和调试基于 ANTLR 的解析器。 ANTLR 为各种宿主语言生成语法,例如JAVA、C、Python、PHP 或 C#。 ActionScript 运行时当前为 损坏。
如果您想自下而上学习如何解析表达式(或一般语言),我建议您这样做Niklaus Wirth 提供的免费书籍文本(或 德语版),Pascal 和 Modula-2 的著名发明者。
You probably want to implement a term rewriting system. Regarding the underlying math, have a look at WikiPedia.
Structure of a term rewrite module
Since I implemented a solution recently...
First, prepare a class CExpression, which models the structure of your expression.
Implement
CRule, which contains a pattern and a replacement. Use special symbols as pattern variables, which need to get bound during pattern matching and replaced in the replacement expression.Then, implement a class
CRule. It's main methodapplyRule(CExpression, CRule)tries to match the rule against any applicable subexpression of expression. In case it matches, return the result.Finaly, implement a class
CRuleSet, which is simply a set of CRule objects. The main methodreduce(CExpression)applies the set of rules as long as no more rules can be applied and then returns the reduced expression.Additionally, you need a class
CBindingEnvironment, which maps already matched symbols to the matched values.Try to rewrite expression to a normal form
Don't forget, that this approach works to a certain point, but is likely to be non complete. This is due to the fact, that all of the following rules perform local term rewrites.
To make this local rewrite logic stronger, one should try to transform expressions into something I'd call a normal form. This is my approach:
If a term contains literal values, try to move the term as far to the right as possible.
Eventually, this literal value may appear rightmost and can be evaluated as part of a fully literal expression.
When to evaluate fully literal expression
An interesting question is when to evaluate fully literal expression. Suppose you have an expression
which would reduce to
Now suppose x gets replaced by 3. This would yield something like
Thus eager evaluation returns a slightly incorrect value.
At the other side, if you keep ( 1 / 3 ) and first replace x by 3
a rewrite rule would give
Thus, it might be useful to evaluate fully literal expression late.
Examples of rewrite rules
Here is how my rules appear inside the application: The _1, _2, ... symbols match any subexpression:
or a bit more complicated
Certain special symbols only match special subexpressions. E.g. _Literal1, _Literal2, ... match only literal values:
This rule moves non-literal expression to the left:
Any name, that begins with a '_', is a pattern variable. While the system matches a rule, it keeps a stack of assignments of already matched symbols.
Finally, don't forget that rules may yield non terminating replacement sequences.
Thus while reducing expression, make the process remember, which intermediate expressions have already been reached before.
In my implementation, I don't save intermediate expressions directly. I keep an array of MD5() hashes of intermediate expression.
A set of rules as a starting point
Here's a set of rules to get started:
Make rules first-class expressions
An interesting point: Since the above rules are special expression, which get correctly evaluate by the expression parser, users can even add new rules and thus enhance the application's rewrite capabilities.
Parsing expressions (or more general: languages)
For Cocoa/OBjC applications, Dave DeLong's DDMathParser is a perfect candidate to syntactically analyse mathematical expressions.
For other languages, our old friends Lex & Yacc or the newer GNU Bison might be of help.
Far younger and with an enourmous set of ready to use syntax-files, ANTLR is a modern parser generator based on Java. Besides purely command-line use, ANTLRWorks provides a GUI frontend to construct and debug ANTLR based parsers. ANTLR generates grammars for various host language, like JAVA, C, Python, PHP or C#. The ActionScript runtime is currently broken.
In case you'd like to learn how to parse expressions (or languages in general) from the bottom-up, I'd propose this free book's text from Niklaus Wirth (or the german book edition), the famous inventor of Pascal and Modula-2.
这个任务可能会变得相当复杂(除了最简单的转换之外)。本质上,这就是代数软件一直在做的事情。
您可以找到有关如何完成此操作的可读介绍(基于规则的评估),例如 Mathematica。
This task can become quite complicated (besides the simplest transformation). Essentially this is what algebra software does all the time.
You can find a readable introduction how this is done (rule-based evaluation) e.g. for Mathematica.
您想要构建一个 CAS(计算代数系统),并且该主题非常广泛,以至于有一个专门的研究领域。这意味着有一些书籍可能会比SO更好地回答您的问题。
我知道有些系统构建的树首先减少常量,然后将树放入标准化形式,然后使用 经过验证/已知公式的大型数据库将问题转化为其他形式。
You're wanting to build a CAS (compute algebra system) and the topic is so wide that there is an entire field of study dedicated to it. Which means there are a few books that will probably answer your question better than SO.
I know some systems build trees that reduce constants first and then put the tree into a normalized form and then use a large database of proven/known formulas to transform the problem into some other form.
我相信你必须“暴力”这样的树。
您必须制定一些规则来描述可能的简化。然后你必须遍历树并搜索适用的规则。由于某些简化可能会导致比其他简化更简单的结果,因此您必须执行与在地铁计划中查找最短路线类似的操作:尝试所有可能性并按某些质量标准对结果进行排序。
由于此类场景的数量是有限的,您可能能够通过尝试运算符和变量的所有组合来自动发现简化规则,并再次使用遗传算法来验证之前是否未找到该规则并且它实际上简化了输入。
乘法可以表示为加法,因此一个规则可能是 a - a 自行抵消: 2a-a = a+aa
另一个规则是首先将所有除法相乘,因为这些是分数。示例:
1/2 + 3/4
找出所有除法,然后将每个分数与所有其他分数两边的除数相乘
4/8 + 6/8
那么所有元素都有相同的除数,因此可以统一为
(4+6)/8 = 10/8
最后你找到顶部和底部之间的最大公约数
5/4
应用于您的树时,策略是从底部叶子向上工作,首先通过将其转换为加法来简化每个乘法。然后像分数一样简化每个加法。
与此同时,您会再次检查您的快捷规则以发现此类简化。要知道规则是否适用,您可能必须尝试子树的所有排列。例如,aa 规则也适用于-a+a。可能有a+ba。
只是一些想法,希望能给你一些想法......
I believe you have to "brute force" such trees.
You will have to formulate a couple of rules that describe possible simplifications. Then you habe to walk through the tree and search for applicable rules. Since some simplifications might lead to simpler results than others you will have to do a similar thing that you do for finding the shortest route on a subway plan: try out all possibilities and sort the results by some quality criteria.
Since the number of such scenarios is finite you might be able to discover the simplification rules automatically by trying out all combinations of operators and variables and again have a genetic algorithm that verifies that the rule has not been found before and that it actually simplifies the input.
Multiplications can be represented as additions, so one rule might be that a - a cancels itself out: 2a-a = a+a-a
Another rule would be to first multiply out all divisions because those are fractions. Example:
1/2 + 3/4
Discover all the divisions and then multiply each fraction with the divisor on both sides of all other fractions
4/8 + 6/8
Then all elements have the same divisor and so can the unified to
(4+6)/8 = 10/8
Finally you find the highest common divisor between top and bottom
5/4
Applied to your tree the strategy would be to work from the bottom leaves upwards simplifying each multiplication first by converting it to additions. Then simplifying each addition like the fractions
All the while you would check agains your shortcut rules to discover such simplifcations. To know that a rule applies you probably have to either try out all permutations of a subtree. E.g. The a-a rule would also apply for -a+a. There might be a a+b-a.
Just some thoughts, hope that gives you some ideas...
实际上,您通常不能这样做,因为尽管它们在数学上是相同的,但在计算机算术中可能不同。例如,-MAX_INT 未定义,因此 --%a =/= %a。同样,对于浮点数,您必须适当处理 NaN 和 Inf。
You actually can't in general do this because, although they are the same mathematically, the may not be the same in computer arithmetic. For instance, -MAX_INT is undefined, so --%a =/= %a. Similarly for floats, you have to deal with NaN and Inf appropriately.
我天真的方法是拥有某种带有每个函数的逆函数的数据结构(即
除和乘)。显然,您需要进一步的逻辑来确保它们实际上是逆的,因为乘以 3 然后除以 4 实际上并不是逆的。虽然这很原始,但我认为这是解决问题的一个不错的第一步,并且可以解决您在问题中提到的许多情况。
我确实期待看到您的完整解决方案,并敬畏地凝视着数学的才华:)
My naive approach would be to have some sort of data structure with inverses of each function (i.e.
divideandmultiply). You would obviously need further logic to make sure they are actually inverse since multiplying by 3 and then dividing by 4 is not actually an inverse.Although this is primitive, I think it's a decent first pass at the problem and would solve a lot of the cases you noted in your question.
I do look forward to seeing your full solution and staring in awe at is mathematical brilliance :)