在一组无序点上放置网格的算法

发布于 2024-12-05 17:28:44 字数 940 浏览 1 评论 0原文

给定一大组（数万到数百万）表示为 3D 笛卡尔向量的无序点，什么是制作包含所有点的规则方形网格（用户定义的间距）的好算法？一些限制：

网格需要是方形和规则的
我需要能够调整网格间距（其中一个正方形的一边的长度），理想情况下使用单个变量
我想要一个最小尺寸的网格，即每个'网格中的“块”应该至少包含一个无序点，并且每个无序点都应该包含在一个“块”中
算法的返回值应该是网格点的坐标列表

为了以二维方式说明，给定这个点集：

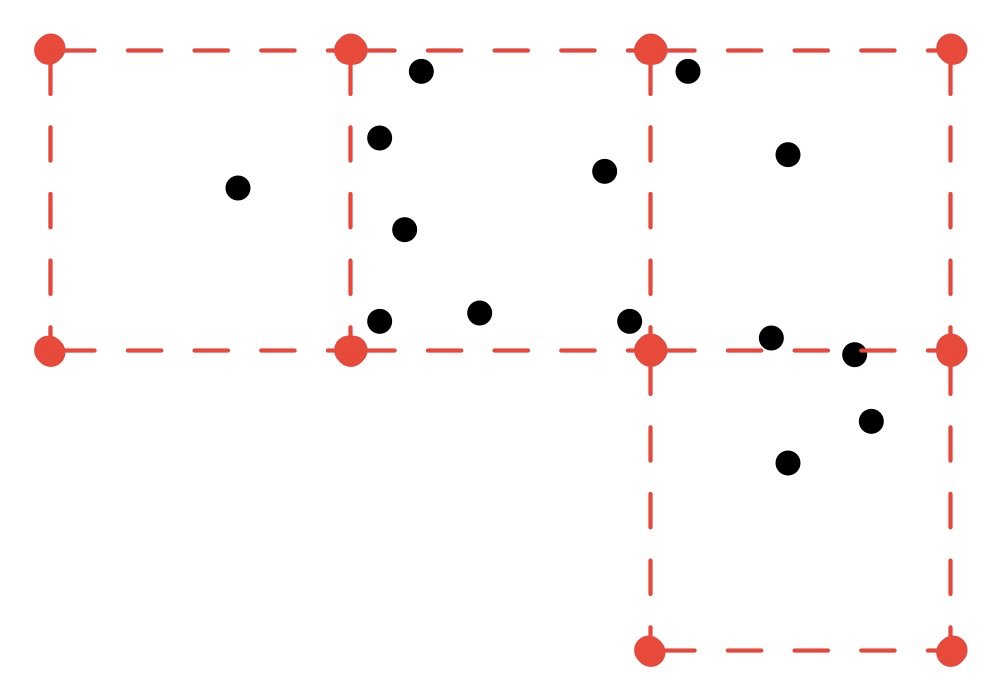
对于某些网格间距 X，算法的一个可能的返回值将是这些红点的坐标（虚线仅用于说明目的）：

对于网格间距 X/2，一个可能的返回值算法的坐标将是这些红点的坐标（虚线仅用于说明目的）：

对于任何感兴趣的人，我正在处理的无序点是原子坐标大蛋白质分子，就像您可以从 .pdb 文件中获得的那样。

尽管伪代码也很好，但 Python 是解决方案的首选。

编辑：我认为我对我需要的东西的第一个描述可能有点模糊，所以我添加了一些约束和图像来澄清事情。

原文

分享到QQ

分享到微博

如果你对这篇内容有疑问，欢迎到本站社区发帖提问参与讨论，获取更多帮助，或者扫码二维码加入 Web 技术交流群。

发布评论

需要登录才能够评论，你可以免费注册一个本站的账号。

梦萦几度 2024-12-12 17:28:44

我建议你制作一个 kd 树。它快速、简单且易于实现：

kd tree

维基百科代码：

class Node: pass

def kdtree(point_list, depth=0):
    if not point_list:
        return

    # Select axis based on depth so that axis cycles through all valid values
    k = len(point_list[0]) # assumes all points have the same dimension
    axis = depth % k

    # Sort point list and choose median as pivot element
    point_list.sort(key=lambda point: point[axis])
    median = len(point_list) // 2 # choose median

    # Create node and construct subtrees
    node = Node()
    node.location = point_list[median]
    node.left_child = kdtree(point_list[:median], depth + 1)
    node.right_child = kdtree(point_list[median + 1:], depth + 1)
    return node

您必须稍微修改它不过，要符合您的限制。

I'd suggest you make a k-d tree. It's fast-ish, simple, and easy to implement:

k-d tree

And Wikipedia code:

class Node: pass

def kdtree(point_list, depth=0):
    if not point_list:
        return

    # Select axis based on depth so that axis cycles through all valid values
    k = len(point_list[0]) # assumes all points have the same dimension
    axis = depth % k

    # Sort point list and choose median as pivot element
    point_list.sort(key=lambda point: point[axis])
    median = len(point_list) // 2 # choose median

    # Create node and construct subtrees
    node = Node()
    node.location = point_list[median]
    node.left_child = kdtree(point_list[:median], depth + 1)
    node.right_child = kdtree(point_list[median + 1:], depth + 1)
    return node

You'd have to slightly modify it, though, to fit within your constraints.

回复收藏 0 原文

浅蓝的眸勾画不出的柔情 2024-12-12 17:28:44

因为您要求用户指定间距的规则方形网格，所以听起来一个相当简单的方法应该可行。

首先通过数据计算出每个维度的最小和最大坐标。计算出覆盖最大值和最小值之间的距离所需的用户指定间距的步数。

再次传递数据，将每个点分配给网格中的一个单元格，使用每个坐标最小值处有一个点和指定间距的网格（例如 X_cell = Math.floor((x_i - x_min) / 间距））。使用字典或数组记录每个单元格中的点数。

现在打印出其中至少有一个点的单元格的坐标。

你确实有一些我没有尝试优化的自由度：除非最小和最大坐标之间的距离是网格间距的精确倍数，否则会有一些倾斜，允许你滑动网格并仍然包含它所有点：目前网格从最低点的位置开始，但它可能在最高点之前结束，因此您有空间在每个维度上将其向下移动一点。当您执行此操作时，某些点将从单元格移动到单元格，并且占用的单元格数量也会发生变化。

如果您一次只考虑一个维度的移动，您可以相当有效地计算出将会发生什么。计算出该维度中每个点与其单元格该维度中的最大坐标之间的距离，然后对这些值进行排序。当您向下移动网格时，与其最大坐标距离最小的点将首先交换单元格，您可以通过按排序顺序移动这些点来逐个迭代它们。如果您在执行此操作时更新单元格中的点数，您可以计算出哪个班次使占用单元格的数量最小化。

当然，您需要担心三个方面。你可以一次处理一个，直到细胞数量减少。这是局部最小值，但可能不是全局最小值。寻找其他局部最小值的一种方法是从随机选择的起点重新开始。

Because you are asking for a regular square grid of user-specified spacing, it sounds like a reasonably straightforward approach should work.

Start by passing through the data to work out the minimum and maximum co-ordinate in each dimension. Work out the number of steps of user-specified spacing required to cover the distance between maximum and minimum.

Pass through the data again to allocate each point to a cell in the grid, using a grid with a point at the minimum of each co-ordinate and the specified spacing (e.g. X_cell = Math.floor((x_i - x_min) / spacing)). Use a dictionary or an array to record the number of points in each cell.

Now print out the co-ordinates of the cells with at least one point in them.

You do have some freedom that I have not attempted to optimise: unless the distance between minimum and maximum co-ordinate is an exact multiple of the grid spacing, there will be some slop that allows you to slide the grid around and still have it contain all the points: at the moment the grid starts at the position of the lowest point, but it probably ends before the highest points, so you have room to move it down a little in each dimension. As you do this, some points will move from cell to cell, and the number of occupied cells will change.

If you consider only moves in one dimension at a time, you can work out what will happen reasonably efficiently. Work out the distance in that dimension between each point and the maximum co-ordinate in that dimension of its cell, and then sort these values. As you move the grid down, the point with the smallest distance to its maximum co-ordinate will swap cells first, and you can iterate through these points one by one by moving through them in sorted order. If you update the counts of points in cells as you do this you can work out which shift minimises the number of occupied cells.

Of course, you have three dimensions to worry about. You could work on them one at a time until you getting reductions in the number of cells. This is a local minimum, but may not be a global minimum. One way to look for other local minima is to start again from a randomly chosen starting point.

回复收藏 0 原文