线性回归,有限制
我有一组点 (x, y),其中每个 y 都有一个误差范围 y.low 到 y.high。假设线性回归是合适的(在某些情况下,数据可能最初遵循幂律,但已被转换为线性)。
计算最佳拟合线很容易,但我需要确保该线对于每个点都保持在误差范围内。如果回归线超出范围,而我只需将其向上或向下推以保持在范围之间,这是可用的最佳拟合,还是斜率也需要更改?
我意识到,在某些情况下,1 个点的下限和另一个点的上限可能需要不同的斜率,在这种情况下,大概只接触这 2 个边界就是最佳拟合。
I have a set of points, (x, y), where each y has an error range y.low to y.high. Assume a linear regression is appropriate (in some cases the data may originally have followed a power law, but has been transformed [log, log] to be linear).
Calculating a best fit line is easy, but I need to make sure the line stays within the error range for every point. If the regressed line goes outside the ranges, and I simply push it up or down to stay between, is this the best fit available, or might the slope need changed as well?
I realize that in some cases, a lower bound of 1 point and an upper bound of another point may require a different slope, in which case presumably just touching those 2 bounds is the best fit.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
与无约束问题相比,所述受约束问题可以具有不同的截距和不同的斜率。
考虑以下示例(实线显示 OLS 拟合):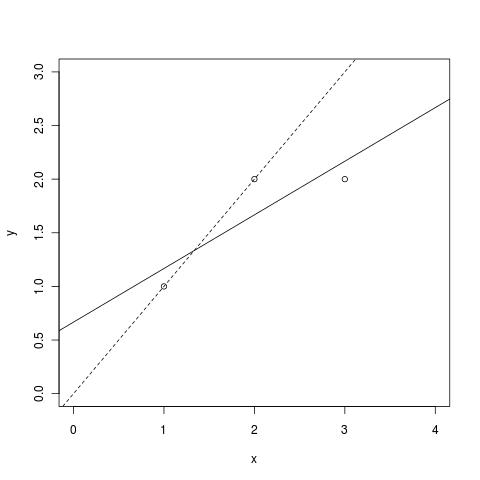
现在,如果您想象非常紧密
[ y.低; y.high]围绕前两个点的边界和最后一个点的边界极其宽松。约束拟合将接近虚线。显然,这两个拟合具有不同的斜率和不同的截距。您的问题本质上是具有线性不等式约束的最小二乘法。例如,在“解决最小二乘问题”中处理了相关算法作者:查尔斯·L·劳森 (Charles L. Lawson) 和理查德·J·汉森 (Richard J. Hanson)。
这是相关章节的直接链接(我希望该链接有效)。您的问题可以简单地转换为问题 LSI(通过将
y.high约束乘以-1)。至于编码,我建议看一下 LAPACK:那里可能已经有一个函数可以解决这个问题(我还没有检查)。
The constrained problem as stated can have both a different intercept and a different slope compared to the unconstrained problem.
Consider the following example (the solid line shows the OLS fit):
Now if you imagine very tight
[y.low; y.high]bounds around the first two points and extremely loose bounds over the last one. The constrained fit would be close to the dotted line. Clearly, the two fits have different slopes and different intercepts.Your problem is essentially the least squares with linear inequality constraints. The relevant algorithms are treated, for example, in "Solving least squares problems" by Charles L. Lawson and Richard J. Hanson.
Here is a direct link to the relevant chapter (I hope the link works). Your problem can be trivially transformed to Problem LSI (by multiplying your
y.highconstraints by-1).As far as coding this up, I'd suggest taking a look at LAPACK: there may already be a function there that solves this problem (I haven't checked).
我知道 MATLAB 有一个优化库,可以执行约束 SQP(顺序二次规划),还有许多其他方法来解决带有不等式约束的二次最小化问题。您想要最小化的成本函数将是您的拟合与数据之间的平方误差之和。限制就是你提到的那些。我确信也有免费的库可以做同样的事情。
I know MATLAB has an optimization library that can do constrained SQP (sequential quadratic programming) and also lots of other methods for solving quadratic minimization problems with inequality constraints. The cost function you want to minimize will be the sum of the squared errors between your fit and the data. The constraints are those you mentioned. I'm sure there are free libraries that do the same thing too.