从多边形的 4 个点计算宽度和高度
我有四个点形成一个矩形,我允许用户移动任何点并将矩形旋转一个角度(这将围绕中心点旋转每个点)。它保持近乎完美的矩形形状(在 PointF 精度允许的范围内)。这是我从四个点绘制的“矩形”的示例:
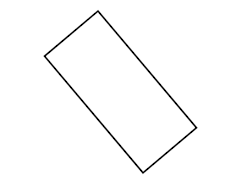
但是,我需要能够获得点之间的宽度和高度。当矩形不旋转时,这很容易,但是一旦旋转它,我的数学就会返回此处红色轮廓所示的宽度和高度:
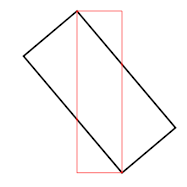
假设我知道点的顺序(例如从左上角顺时针方向),如何检索它们代表的矩形的宽度和高度?
I have four points which form a rectangle, and I am allowing the user to move any point and to rotate the rectangle by an angle (which rotates each point around the center point). It stays in near-perfect Rectangle shape (as far as PointF precision allows). Here's an example of my "rectangle" drawn from four points:

However, I need to be able to get the width and height between the points. This is easy when the rectangle is not rotated, but once I rotate it my math returns the width and height shown by the red outline here:

Assuming I know the order of the points (clockwise from top-left for example), how do I retrieve the width and the height of the rectangle they represent?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(3)
如果“宽度”和“高度”只是指边长,并且列表或数组中有 4 个 PointF 结构,则可以执行以下操作:
If by "width" and "height", you just mean the edge lengths, and you have your 4
PointFstructures in a list or array, you can do:只需使用两点之间距离的算法即可。
如果有 A、B、C、D 点,您将得到两个距离。
sqrt((Bx-Ax)^2 + (By-Ay)^2)将等于sqrt((Dx-Cx)^2 + (Dy-Cy)^2)sqrt((Cx-Bx)^2 + (Cy-By)^2)将等于sqrt((Ax-Dx)^2 + (Ay-Dy)^2)选择一项作为您的宽度,一项作为您的高度。
Just use the algorithm for the distance between two points.
If you have points A, B, C, D, you will get two distances.
sqrt((Bx-Ax)^2 + (By-Ay)^2)will be equal tosqrt((Dx-Cx)^2 + (Dy-Cy)^2)sqrt((Cx-Bx)^2 + (Cy-By)^2)will be equal tosqrt((Ax-Dx)^2 + (Ay-Dy)^2)Pick one to be your width and one to be your height.
假设最上面的角是 A。然后将其他边逆时针命名为 ABCD
矩形宽度 = A 和 B 之间的距离
矩形的高度 = B 和 C 之间的距离
计算 A(x1,y1) 和 B(x2,y2) 两点之间距离的公式为:
其中 d 是距离。
Let's say top-most corner is A. Then name other edges anti-clockwise as ABCD
width of rectangle = distance between A and B
height of rectangle = distance between B and C
Formula to find distance between two points say A(x1,y1) and B(x2,y2) is:
where d is distance.