Mathematica 的编程挑战

Question

我正在将外部程序与 Mathematica 连接。我正在为外部程序创建一个输入文件。它是将 Mathematica 生成的图形中的几何数据转换为预定义的格式。这是一个几何示例。

图 1

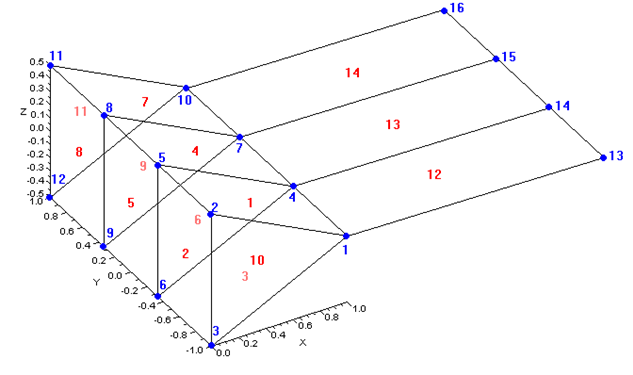
在 Mathematica 中可以通过多种方式描述几何图形。一种费力的方法如下。

dat={{1.,-1.,0.},{0.,-1.,0.5},{0.,-1.,-0.5},{1.,-0.3333,0.},{0.,-0.3333,0.5},
{0.,-0.3333,-0.5},{1.,0.3333,0.},{0.,0.3333,0.5},{0.,0.3333,-0.5},{1.,1.,0.},
{0.,1.,0.5},{0.,1.,-0.5},{10.,-1.,0.},{10.,-0.3333,0.},{10.,0.3333,0.},{10.,1.,0.}};

Show[ListPointPlot3D[dat,PlotStyle->{{Red,PointSize[Large]}}],Graphics3D[{Opacity[.8],
Cyan,GraphicsComplex[dat,Polygon[{{1,2,5,4},{1,3,6,4},{2,3,6,5},{4,5,8,7},{4,6,9,7},
{5,6,9,8},{7,8,11,10},{7,9,12,10},{8,9,12,11},{1,2,3},{10,12,11},{1,4,14,13},
{4,7,15,14},{7,10,16,15}}]]}],AspectRatio->GoldenRatio]

这会生成 MMA 的 GraphicsComplex 格式所需的 3D 几何图形。

此几何图形被描述为我的外部程序的以下输入文件。

# GEOMETRY
# x y z [m]
NODES 16
1. -1. 0.
0. -1. 0.5
0. -1. -0.5
1. -0.3333 0.
0. -0.3333 0.50. -0.3333 -0.5
1. 0.3333 0.
0. 0.3333 0.5
0. 0.3333 -0.5
1. 1. 0.
0. 1. 0.5
0. 1. -0.5
10. -1. 0.
10. -0.3333 0.
10. 0.3333 0.
10. 1. -0.
# type node_id1 node_id2 node_id3 node_id4  elem_id1 elem_id2 elem_id3 elem_id4
PANELS 14
1 1 4 5 2 4 2 10 0
1 2 5 6 3 1 5 3 10
1 3 6 4 1 2 6 10 0
1 4 7 8 5 7 5 1 0
1 5 8 9 6 4 8 6 2
1 6 9 7 4 5 9 3 0
1 7 10 11 8 8 4 11 0
1 8 11 12 9 7 9 5 11
1 9 12 10 7 8 6 11 0
2 1 2 3 1 2 3
2 10 12 11 9 8 7
10 4 1 13 14 1 3
10 7 4 14 15 4 6
10 10 7 15 16 7 9
# end of input file

现在我从这个外部程序的文档中得到的描述非常简短。我在这里引用它。

---

1. 第一个关键字 NODES 表示节点总数 节点。此行之后不应有任何注释或空行。接下来的几行包括 x、y、z 三个值节点坐标和行数必须与 number 相同 节点数。
2. 下一个关键字是PANEL，说明我们有多少个面板。之后我们有线路 定义每个面板。第一个整数定义面板类型
3. ID 1 - 四边形面板 - 由四个节点和四个相邻面板定义。 相邻面板是共享相同边（节点对）的面板，并且需要 速度和压力计算（方法 1 和 2）。缺少邻居（例如 后缘附近的面板）填充值 0（参见图 1）。
4. ID 2 - 三角形面板 - 由三个节点和三个相邻面板定义。
5. ID 10 - 尾流面板 - 是由四个节点和两个节点定义的四边形面板 位于后缘的（相邻）面板（尾流面板所在的面板） 应用库塔条件）。
6. 面板类型 1 和 2 必须在输入文件中的类型 10 之前定义。 需要注意的是表面法线；定义面板的节点顺序应该是 逆时针。根据右手定则，如果手指弯曲以遵循编号， 拇指将显示应指向“向外”几何体的法线向量。

---

挑战！！

我们在名为 One.obj 的文件中获得了 3D CAD 模型，并且可以正常导出综合格斗。

cd = Import["One.obj"]

输出是 MMA Graphics3D 对象

现在，当 MMA 内部读取几​​何数据时，我可以轻松访问它们。

{ver1, pol1} = cd[[1]][[2]] /. GraphicsComplex -> List;
MyPol = pol1 // First // First;
Graphics3D[GraphicsComplex[ver1,MyPol],Axes-> True]

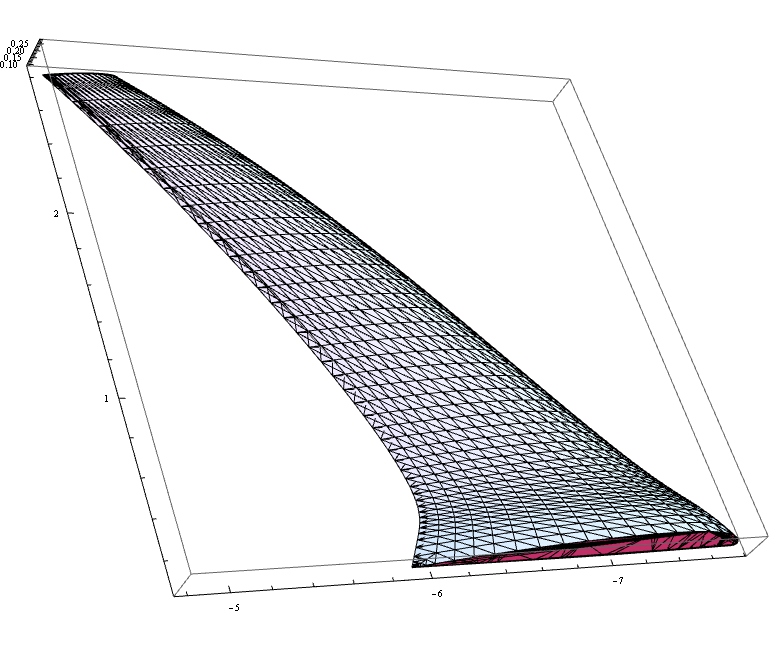
1. 我们如何使用 ver1 和 中包含的顶点和多边形信息>pol1 并将它们写入文本文件，如上面输入文件示例中所述。在这种情况下，我们将只有 ID2 类型（三角形）面板。
2. 使用 Mathematica 三角测量如何找到此 3D 对象的表面积。 MMA 中是否有可以计算表面积的内置函数？
3. 现在无需创建唤醒面板或 ID10 类型元素。仅包含三角形元素的输入文件就可以了。

---

抱歉发了这么长的帖子，但这是我长期以来一直试图解决的一个难题。希望你们中的一些专家能够有正确的洞察力来破解它。

BR

Answer 1

Q1 和 Q2 很简单，您可以在问题中删除“挑战”标签。第三季度可能需要一些澄清。

Q1

edges = cd[[1, 2, 1]];

polygons = cd[[1, 2, 2, 1, 1, 1]];

---

更新Q1

主要问题是找到每个多边形的邻居。以下代码执行此操作：

(* Split every triangle in 3 edges, with nodes in each edge sorted *)
triangleEdges = (Sort /@ Subsets[#, {2}]) & /@ polygons;

(* Generate a list of edges *)
singleEdges = Union[Flatten[triangleEdges, 1]];

(* Define a function which, given an edge (node number list), returns the bordering  *)
(* triangle numbers. It's done by working through each of the triangles' edges       *)
ClearAll[edgesNeighbors]
edgesNeighbors[_] = {};
MapIndexed[(
   edgesNeighbors[#1[[1]]] = Flatten[{edgesNeighbors[#1[[1]]], #2[[1]]}];
   edgesNeighbors[#1[[2]]] = Flatten[{edgesNeighbors[#1[[2]]], #2[[1]]}];
   edgesNeighbors[#1[[3]]] = Flatten[{edgesNeighbors[#1[[3]]], #2[[1]]}];
   ) &, triangleEdges
];

(* Build a triangle relation table. Each '1' indicates a triangle relation *)
relations = ConstantArray[0, {triangleEdges // Length, triangleEdges // Length}];
Scan[
  (n = edgesNeighbors[##]; 
     If[Length[n] == 2, 
        {n1, n2} = n; 
        relations[[n1, n2]] = 1;  relations[[n2, n1]] = 1];
   ) &, singleEdges
]

MatrixPlot[relations]

(* Build a neighborhood list *)
triangleNeigbours = 
    Table[Flatten[Position[relations[[i]], 1]], {i,triangleEdges // Length}];

(* Test: Which triangles border on triangle number 1? *)
triangleNeigbours[[1]]

(* ==> {32, 61, 83} *)

(* Check this *)
polygons[[{1, 32, 61, 83}]]

(* ==> {{1, 2, 3}, {3, 2, 52}, {1, 3, 50}, {19, 2, 1}} *)
(* Indeed, they all share an edge with #1 *)

---

您可以使用描述的低级输出函数此处 输出这些。我将把细节留给你（这是我对你的挑战）。

第二季度
机翼的面积是各个多边形的面积之和。各个面积的计算方法如下：

ClearAll[polygonArea];
polygonArea[pts_List] :=
 Module[{dtpts = Append[pts, pts[[1]]]},
   If[Length[pts] < 3, 
      0, 
      1/2 Sum[Det[{dtpts[[i]], dtpts[[i + 1]]}], {i, 1, Length[dtpts] - 1}]
   ]
 ]

基于此 Mathworld 页面。

顺便说一句，该区域已签名，因此您可能需要使用 Abs。

更正
上述面积函数仅适用于二维中的一般多边形。对于 3D 中三角形的面积，可以使用以下公式：

ClearAll[polygonArea];
polygonArea[pts_List?(Length[#] == 3 &)] := 
    Norm[Cross[pts[[2]] - pts[[1]], pts[[3]] - pts[[1]]]]/2