给定从 Kinect 深度图获得的两个连续的 3D 点云 1 和 2(不是整个云,例如使用 OpenCV 的 GoodFeaturesToMatch 从云中选择的 100 个点),我想计算相机从 1 到 2 的单应性。我知道这是一个投影变换,并且已经有很多人完成了:此处(幻灯片 12),此处(幻灯片 30) 和 这里似乎是经典论文。我的问题是,虽然我是一名称职的程序员,但我没有数学或三角技能将其中一种方法转化为代码。由于这不是一个简单的问题,我为解决以下问题的代码提供了大量赏金:
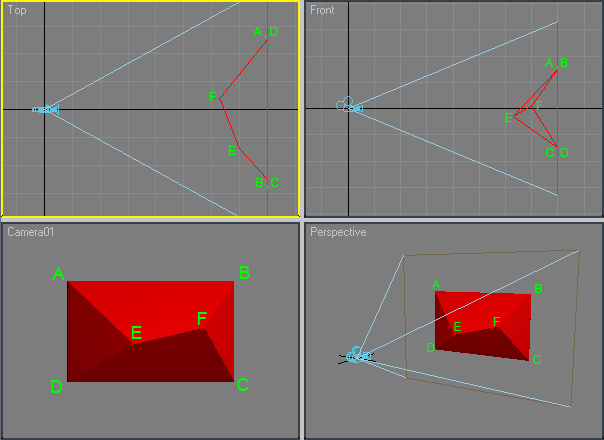
相机位于原点,朝 Z 方向看,在不规则五面体 [A,B,C,D,E,F ]:
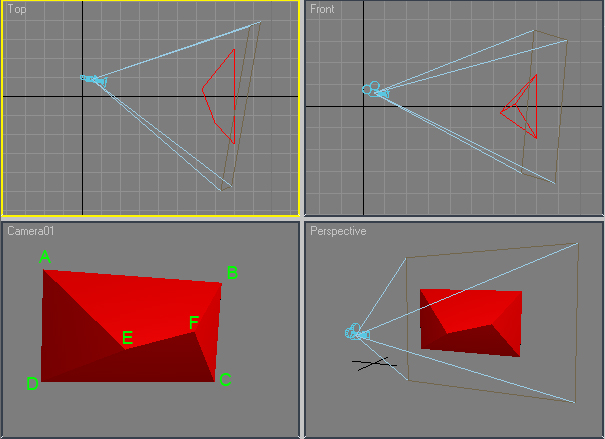
相机向左移动 -90mm (X),向上移动 +60mm (Y),向前移动 +50mm ( Z)并向下旋转 5°,向右旋转 10°,逆时针旋转 -3°:
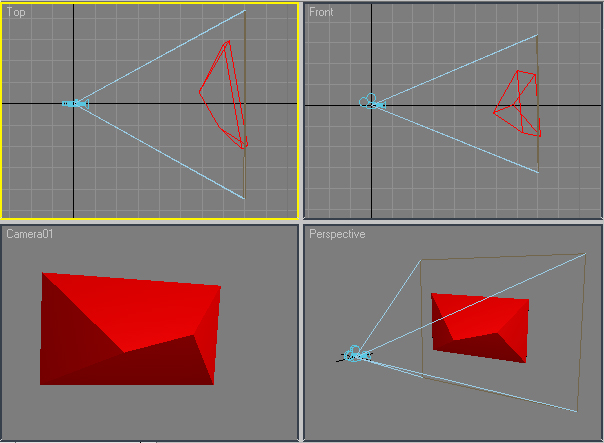
旋转整个场景,使相机回到原来的位置,让我能够确定顶点的位置2:
用于准备此内容的 3DS Max 文件为 最大 1, 最大限度2 和 max 3
这是之前和之后的顶点位置,内在函数等:
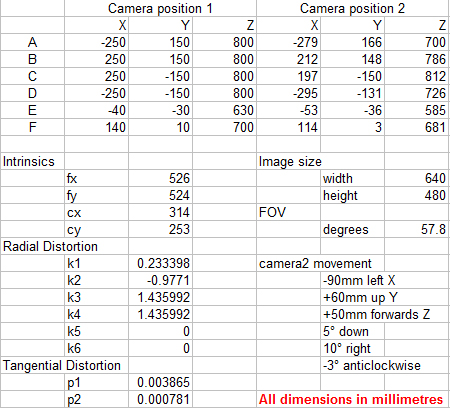
请注意,camera2 的顶点并非 100% 准确,存在一些故意的噪声。
这是 Excel 文件中的数字
我需要的代码,必须易于翻译进入 VB.Net 或 C#,在必要时使用 EMGUCV 和 OpenCV,获取 2 组顶点和内在函数并生成以下输出:
Camera 2 is at -90 X, +60 Y, +50 Z rotated -5 Y, 10 X, -3 Z.
The homography matrix to translate points in A to B is:
a1, a2, a3
b1, b2, b3
c1, c2, c3
我不知道单应性是 3X3 还是 3X4对于齐次坐标,但它必须允许我将顶点从 1 平移到 2。
我也不知道 a1、a2 等值;这就是你必须找到的>;-)
500 赏金报价“取代”了我向 提供的赏金,这非常相似问题,我在那里添加了一条指向这个问题的评论。
EDIT2:我想知道我问这个问题的方式是否具有误导性。在我看来,问题更多的是点云拟合而不是相机几何(如果你知道如何将 A 平移和旋转到 B,你就知道相机变换,反之亦然)。如果是这样,那么也许可以使用卡布什算法或类似的算法来获得解决方案
Given two consecutive 3D point clouds 1 and 2 (not the whole cloud, say 100 points selected from the cloud with OpenCV's GoodFeaturesToMatch), obtained from a Kinect depthmap, I want to compute camera's homography from 1 to 2. I understand that this a projective transform, and it has already been done by many people: here (slide 12), here (slide 30) and here in what seems to be the classic paper. My problem is that whilst I'm a competent programmer, I haven't got the math or trig skills to turn one of those methods into code. As this is not an easy problem, I offer a large bounty for the code that solves the following problem:
The camera is at the origin, looking in the Z direction, at irregular pentahedron [A,B,C,D,E,F]:

The camera moves -90mm to the left (X), +60mm up (Y), +50mm forwards (Z) and rotates 5° down, 10° right and -3° anticlockwise:

Rotating the entire scene so that the camera is back at its original position allow me to determine the vertices' locations at 2:

The 3DS Max files used to prepare this are max 1, max 2 and max 3
Here are the vertices' positions before and after, the intrinsics, etc.:

Note that camera2's vertices are not 100% accurate, there's a bit of deliberate noise.
here are the numbers in an Excel file
The code I need, which must be readily translatable into VB.Net or C#, using EMGUCV and OpenCV where necessary, takes the 2 sets of vertices and the intrinsics and produces this output:
Camera 2 is at -90 X, +60 Y, +50 Z rotated -5 Y, 10 X, -3 Z.
The homography matrix to translate points in A to B is:
a1, a2, a3
b1, b2, b3
c1, c2, c3
I don't know if the homography is 3X3 or 3X4 for homogenous coordinates, but it must allow me to translate the vertices from 1 to 2.
I also don't know the values a1, a2, etc; that's what you have to find >;-)
The 500 bounty offer 'replaces' the bounty I offered to this very similar question, I've added a comment there pointing to this question.
EDIT2: I'm wondering if the way I'm asking this question is misleading. It seems to me that the problem is more of point-cloud fitting than of camera geometry (if you know how to translate and rotate A to B, you know the camera transform and vice-versa). If so, then perhaps the solution could be obtained with Kabsch's algorithm or something similar






发布评论
评论(3)
用于计算 2D 或 3D 点云的两个快照之间的差异的“正确”算法称为 ICP(迭代最近点)。 解决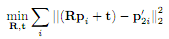 问题
问题
该算法以人类可读格式 :对于给定的点集 P1 和 P2,找到旋转矩阵 R 和平移矩阵 T将 P1 转换为 P2。只要确保它们围绕其起源进行标准化即可。
对于那些感兴趣的人来说,这是计算几何处理中的一个主题
"The correct" algorithm to use for computing difference between two snapshots of 2D or 3D point clouds is called ICP (Iterative Closest Point). The algorithm solves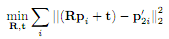
In human-readable-format: For given point sets P1 and P2 find the rotation matrix R and translation T that transforms P1 to P2. Just make sure they are normalized around their origin.
For those interested this is a topic within Computational Geometry Processing
对于那些有类似需求的人,这里有一个使用 Kabsch 算法来确定 3D 几何图形的平移和最佳旋转的部分解决方案:
输出:
但我仍然不知道如何确定相机的位置。
For those with similar needs, here's a partial solution using Kabsch's algorithm to determine the translation and optimal rotation of a piece of 3D geometry:
Output:
but I still can't figure out how to determine the camera's position.
迭代最近点算法 (ICP) 现在是用于 C#/VB 的官方 Kinect SDK 1.7 的一部分,
那么在 VB 中恢复相机姿势就非常容易了。
http://www.microsoft.com/en-us/kinectforwindows/develop /new.aspx
The Iterative Closest Point algorithm (ICP) is now a part of the official Kinect SDK 1.7 for C#/VB
Recovery of camera pose in VB is pretty easy then.
http://www.microsoft.com/en-us/kinectforwindows/develop/new.aspx