计算曲线上的点
是否可以计算曲线的中间点...这是我的镜像
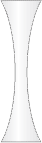
在上图中.是否可以通过知道起点和终点来计算中间点(一侧)
Is it possible to calculate intermediate points of a curve...Here is my mirror image
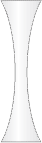
In the above image.Is it possible to calculate the intermediate points(one side) by knowing starting and ending point
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(1)
如果您对曲线有所了解,那么这一切都取决于您对曲线的了解(起点和终点、初始斜率、中心点等)。通常有两种方法:
如果您知道曲线方程,则可以准确地做到这一点。通常这样的曲线要么是圆形,要么是贝塞尔曲线,如果你知道它是其中,只需给定几个点,您就可以精确地拟合所有其他点。
您还可以进行三次样条拟合。这是拟合平滑曲线的标准方法,因此执行此操作的包非常常见。在这样的平滑曲线上,给出端点,比如说中间点,拟合将几乎是精确的。 (在这里,您基本上最终得到了贝塞尔曲线,尽管参数化有点不同。)
If you know something about the curve it is, and it all depends on what you know about the curve (start and end points, initial slopes, center points, etc). There are generally two approaches:
If you know the equation of the curve, it's possible to do this exactly. Commonly curves like this are either circles or Bezier curves, and if you know it's either of these, you can fit all the other points exactly just given a few.
You can also do a cubic spline fit. This is a standard approach to fitting smooth curves so packages to do this are very common. On a smooth curve like this, give then end points, and, say, the middle point, the fit will be almost exact. (Here, you essentially end up with a Bezier curve, though parametrized a bit differently.)