绘制具有不同大小箱的概率热图/hexbin

发布于 2024-12-03 05:48:02 字数 2953 浏览 0 评论 0原文

我有这个图形（由下面的 R 代码生成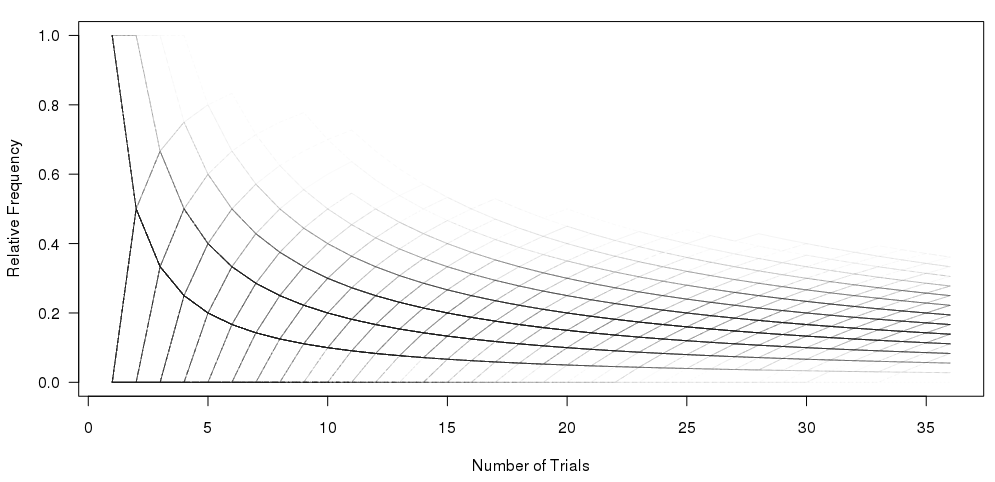）： multisample

#Set the number of bets and number of trials and % lines
numbet <- 36 
numtri <- 1000 
#Fill a matrix where the rows are the cumulative bets and the columns are the trials
xcum <- matrix(NA, nrow=numbet, ncol=numtri)
for (i in 1:numtri) {
x <- sample(c(0,1), numbet, prob=c(5/6,1/6), replace = TRUE)
xcum[,i] <- cumsum(x)/(1:numbet)
}
#Plot the trials as transparent lines so you can see the build up
matplot(xcum, type="l", xlab="Number of Trials", ylab="Relative Frequency", main="", col=rgb(0.01, 0.01, 0.01, 0.02), las=1)

我非常喜欢这个图的构建方式并将更频繁的路径显示为比罕见的路径更暗（但对于打印演示来说不够清晰）。我想做的是为数字生成某种十六进制或热图。考虑一下，似乎该图必须包含不同大小的垃圾箱（请参阅我的信封背面草图）：

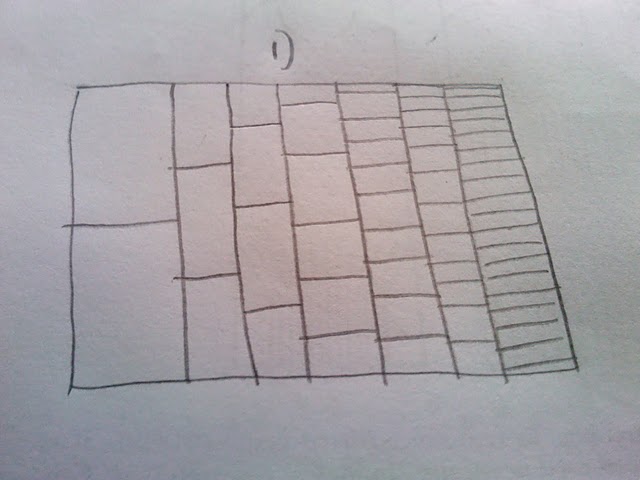
binsketch

那么我的问题是：如果我使用上面的代码模拟一百万次运行，我如何将其呈现为热图或十六进制，并具有草图中所示的不同大小的垃圾箱？

澄清一下：我不想依赖透明度以显示审判通过情节的一部分的罕见性。相反，我想用热来表示稀有性，并将常见路径显示为热（红色），将罕见路径显示为冷（蓝色）。另外，我认为垃圾箱的大小不应该相同，因为第一个试验只有两个可以放置路径的地方，但最后一个试验有更多的地方。因此，基于这一事实，我选择了不断变化的仓秤。 本质上，我正在计算路径经过单元格的次数（第 1 列中 2 次，第 2 列中 3 次等），然后根据经过的次数对单元格进行着色。

更新：我已经有一个类似于@Andrie的情节，但我不确定它比上面的情节更清晰。我不喜欢该图的不连续性质（也是我想要某种热图的原因）。我认为因为第一列只有两个可能的值，所以它们之间不应该有巨大的视觉间隙等等。因此我设想了不同大小的垃圾箱。我仍然认为分箱版本会更好地显示大量样本。

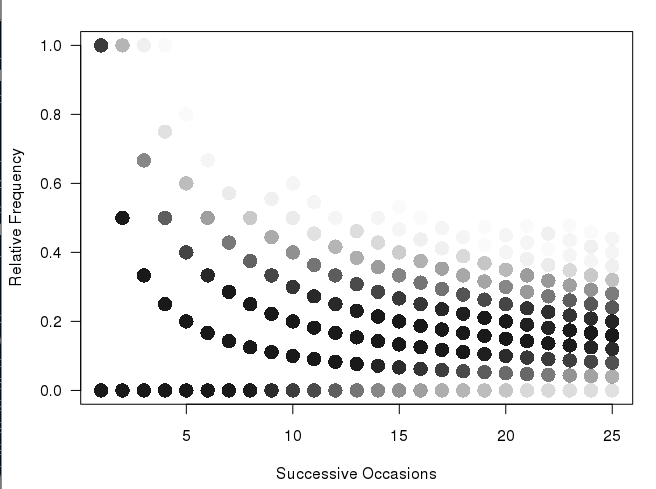
plot2

更新：此网站概述了绘制热图的过程：

要创建密度（热图）图版本，我们必须有效地枚举这些点在图像中每个离散位置的出现情况。这是通过设置一个网格并计算点坐标“落入”该网格中每个位置的每个单独像素“箱”的次数来完成的。

也许该网站上的一些信息可以与我们已有的信息结合起来？

更新：我采纳了 Andrie 写的一些内容问题，达到这个，这与我的设想非常接近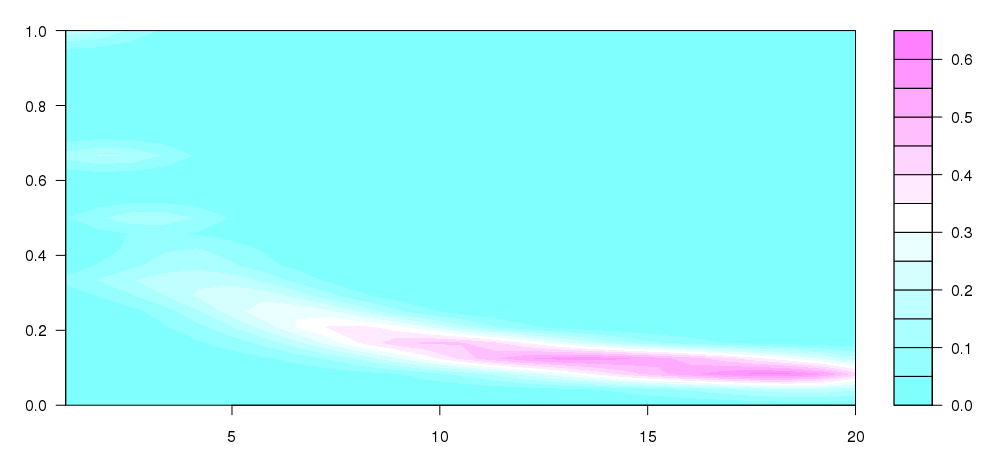： heatmap

numbet <- 20
numtri <- 100
prob=1/6
#Fill a matrix 
xcum <- matrix(NA, nrow=numtri, ncol=numbet+1)
for (i in 1:numtri) {
  x <- sample(c(0,1), numbet, prob=c(prob, 1-prob), replace = TRUE)
  xcum[i, ] <- c(i, cumsum(x)/cumsum(1:numbet))
}
colnames(xcum) <- c("trial", paste("bet", 1:numbet, sep=""))

mxcum <- reshape(data.frame(xcum), varying=1+1:numbet, 
  idvar="trial", v.names="outcome", direction="long", timevar="bet")

 #from the other question
 require(MASS)
dens <- kde2d(mxcum$bet, mxcum$outcome)
filled.contour(dens)

我不太明白发生了什么，但这似乎更像是我想要制作的（显然没有不同尺寸的垃圾箱）。

更新：这与这里的其他图类似。这不太正确：

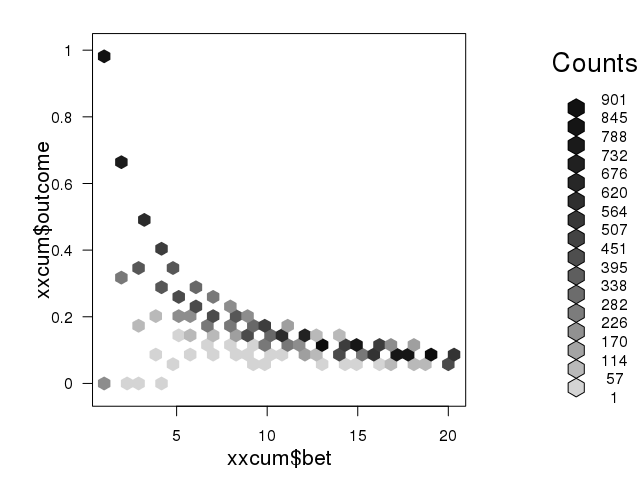
hexbin

plot(hexbin(x=mxcum$bet, y=mxcum$outcome))

最后一次尝试。如上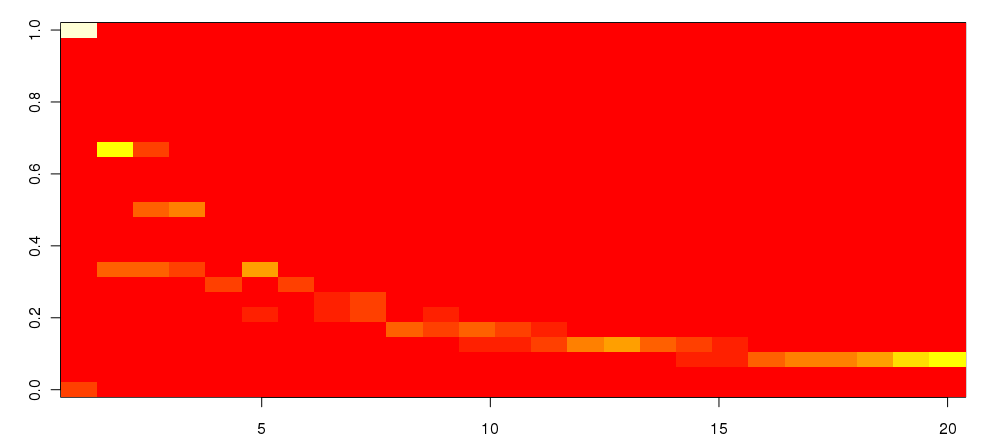：在此处输入图像描述

image(mxcum$bet, mxcum$outcome)

这非常好。我只是希望它看起来像我的手绘草图。

原文

This is related to another question: Plot weighted frequency matrix.

I have this graphic (produced by the code below in R): multisample

#Set the number of bets and number of trials and % lines
numbet <- 36 
numtri <- 1000 
#Fill a matrix where the rows are the cumulative bets and the columns are the trials
xcum <- matrix(NA, nrow=numbet, ncol=numtri)
for (i in 1:numtri) {
x <- sample(c(0,1), numbet, prob=c(5/6,1/6), replace = TRUE)
xcum[,i] <- cumsum(x)/(1:numbet)
}
#Plot the trials as transparent lines so you can see the build up
matplot(xcum, type="l", xlab="Number of Trials", ylab="Relative Frequency", main="", col=rgb(0.01, 0.01, 0.01, 0.02), las=1)

I very much like the way that this plot is built up and shows the more frequent paths as darker than the rarer paths (but it is not clear enough for a print presentation). What I would like to do is to produce some kind of hexbin or heatmap for the numbers. On thinking about it, it seems that the plot will have to incorporate different sized bins (see my back of the envelope sketch):

binsketch

My question then: If I simulate a million runs using the code above, how can I present it as a heatmap or hexbin, with the different sized bins as shown in the sketch?

To clarify: I do not want to rely on transparency to show the rarity of a trial passing through a part of the plot. Instead I would like to denote rarity with heat and show a common pathway as hot (red) and a rare pathway as cold (blue). Also, I do not think the bins should be the same size because the first trial has only two places where the path can be, but the last has many more. Hence the fact I chose a changing bin scale, based on that fact. Essentially I am counting the number of times a path passes through the cell (2 in col 1, 3 in col 2 etc) and then colouring the cell based on how many times it has been passed through.

UPDATE: I already had a plot similar to @Andrie, but I am not sure it is much clearer than the top plot. It is the discontinuous nature of this graph, that I do not like (and why I want some kind of heatmap). I think that because the first column has only two possible values, that there should not be a huge visual gap between them etc etc. Hence why I envisaged the different sized bins. I still feel that the binning version would show large number of samples better.

plot2

Update: This website outlines a procedure to plot a heatmap:

To create a density (heatmap) plot version of this we have to effectively enumerate the occurrence of these points at each discrete location in the image. This is done by setting a up a grid and counting the number of times a point coordinate "falls" into each of the individual pixel "bins" at every location in that grid.

Perhaps some of the information on that website can be combined with what we have already?

Update: I took some of what Andrie wrote with some of this question, to arrive at this, which is quite close to what I was conceiving:
heatmap

numbet <- 20
numtri <- 100
prob=1/6
#Fill a matrix 
xcum <- matrix(NA, nrow=numtri, ncol=numbet+1)
for (i in 1:numtri) {
  x <- sample(c(0,1), numbet, prob=c(prob, 1-prob), replace = TRUE)
  xcum[i, ] <- c(i, cumsum(x)/cumsum(1:numbet))
}
colnames(xcum) <- c("trial", paste("bet", 1:numbet, sep=""))

mxcum <- reshape(data.frame(xcum), varying=1+1:numbet, 
  idvar="trial", v.names="outcome", direction="long", timevar="bet")

 #from the other question
 require(MASS)
dens <- kde2d(mxcum$bet, mxcum$outcome)
filled.contour(dens)

I don't quite understand what's going on, but this seems to be more like what I wanted to produce (obviously without the different sized bins).

Update: This is similar to the other plots here. It is not quite right:

hexbin

plot(hexbin(x=mxcum$bet, y=mxcum$outcome))

Last try. As above:
enter image description here

image(mxcum$bet, mxcum$outcome)

This is pretty good. I would just like it to look like my hand-drawn sketch.

分享到QQ

分享到微博

如果你对这篇内容有疑问，欢迎到本站社区发帖提问参与讨论，获取更多帮助，或者扫码二维码加入 Web 技术交流群。

发布评论

需要登录才能够评论，你可以免费注册一个本站的账号。

我早已燃尽 2024-12-10 05:48:02

编辑

我认为以下解决方案可以满足您的要求。

（请注意，这很慢，尤其是 reshape 步骤）

numbet <- 32
numtri <- 1e5
prob=5/6
#Fill a matrix 
xcum <- matrix(NA, nrow=numtri, ncol=numbet+1)
for (i in 1:numtri) {
  x <- sample(c(0,1), numbet, prob=c(prob, 1-prob), replace = TRUE)
  xcum[i, ] <- c(i, cumsum(x)/cumsum(1:numbet))
}
colnames(xcum) <- c("trial", paste("bet", 1:numbet, sep=""))

mxcum <- reshape(data.frame(xcum), varying=1+1:numbet, 
  idvar="trial", v.names="outcome", direction="long", timevar="bet")


library(plyr)
mxcum2 <- ddply(mxcum, .(bet, outcome), nrow)
mxcum3 <- ddply(mxcum2, .(bet), summarize, 
                ymin=c(0, head(seq_along(V1)/length(V1), -1)), 
                ymax=seq_along(V1)/length(V1),
                fill=(V1/sum(V1)))
head(mxcum3)

library(ggplot2)

p <- ggplot(mxcum3, aes(xmin=bet-0.5, xmax=bet+0.5, ymin=ymin, ymax=ymax)) + 
    geom_rect(aes(fill=fill), colour="grey80") + 
    scale_fill_gradient("Outcome", formatter="percent", low="red", high="blue") +
    scale_y_continuous(formatter="percent") +
    xlab("Bet")

print(p)

Edit

I think the following solution does what you ask for.

(Note that this is slow, especially the reshape step)

numbet <- 32
numtri <- 1e5
prob=5/6
#Fill a matrix 
xcum <- matrix(NA, nrow=numtri, ncol=numbet+1)
for (i in 1:numtri) {
  x <- sample(c(0,1), numbet, prob=c(prob, 1-prob), replace = TRUE)
  xcum[i, ] <- c(i, cumsum(x)/cumsum(1:numbet))
}
colnames(xcum) <- c("trial", paste("bet", 1:numbet, sep=""))

mxcum <- reshape(data.frame(xcum), varying=1+1:numbet, 
  idvar="trial", v.names="outcome", direction="long", timevar="bet")


library(plyr)
mxcum2 <- ddply(mxcum, .(bet, outcome), nrow)
mxcum3 <- ddply(mxcum2, .(bet), summarize, 
                ymin=c(0, head(seq_along(V1)/length(V1), -1)), 
                ymax=seq_along(V1)/length(V1),
                fill=(V1/sum(V1)))
head(mxcum3)

library(ggplot2)

p <- ggplot(mxcum3, aes(xmin=bet-0.5, xmax=bet+0.5, ymin=ymin, ymax=ymax)) + 
    geom_rect(aes(fill=fill), colour="grey80") + 
    scale_fill_gradient("Outcome", formatter="percent", low="red", high="blue") +
    scale_y_continuous(formatter="percent") +
    xlab("Bet")

print(p)

enter image description here

回复收藏 0 原文

眼中杀气 2024-12-10 05:48:02

仅供参考：这更多的是扩展评论而不是答案。

对我来说，这个新图看起来像一个堆叠条形图，其中每个条形图的高度等于下一次试验时上下线的交点。

在此处输入图像描述

我处理此问题的方法是将“试验”视为分类变量。然后我们可以在 xcum 的每一行中搜索相等的元素。如果是，那么我们可以认为这是一个交点，其最小值也代表定义条形高度的倍数。

x <- t(xcum)
x <- x[duplicated(x),]
x[x==0] <- NA

现在我们有了实际点的倍数，我们需要弄清楚如何将其带到下一步并找到一种对信息进行分类的方法。这意味着我们需要决定代表每个分组的点数。让我们为后人写下一些要点。

Trial 1 (2) = 1, 0.5 # multiple = 0.5
Trial 2 (3) = 1, 0.66, 0.33 #  multiple = 0.33
Trial 3 (4) = 1, 0.75, 0.5, 0.25 # multiple = 0.25
Trial 4 (5) = 1, 0.8,  0.6, 0.4, 0.2 # multiple = 0.2
Trial 5 (6) = 1, 0.8333335, 0.6666668, 0.5000001, 0.3333334, 0.1666667
... 
Trial 36 (35) = 1, 0.9722223, ..., 0.02777778 # mutiple = 0.05555556 / 2

换句话说，对于每个试验，有 n-1 个点要绘制。在您的绘图中，您有 7 个垃圾箱。所以我们需要计算出每个 bin 的倍数。

让我们作弊，将最后两列除以二，通过目视检查我们知道最小值低于 0.05

x[,35:36] <- x[,35:36] / 2

然后找到每列的最小值：

x <- apply(x, 2, function(x) min(x, na.rm=T))[-1] # Drop the 1
x <- x[c(1,2,3,4,8,17,35)] # I'm just guessing here by the "look" of your drawing.

最清晰的方法是单独创建每个 bin。显然，这可以稍后自动完成。记住每个点都是

bin1 <- data.frame(bin = rep("bin1",2), Frequency = rep(x[1],2))
bin2 <- data.frame(bin = rep("bin2",3), Frequency = rep(x[2],3))
bin3 <- data.frame(bin = rep("bin3",4), Frequency = rep(x[3],4))
bin4 <- data.frame(bin = rep("bin4",5), Frequency = rep(x[4],5))
bin5 <- data.frame(bin = rep("bin5",9), Frequency = rep(x[5],9))
bin6 <- data.frame(bin = rep("bin6",18), Frequency = rep(x[6],18))
bin7 <- data.frame(bin = rep("bin7",36), Frequency = rep(x[7],36))

df <- rbind(bin1,bin2,bin3,bin4,bin5,bin6,bin7)
ggplot(df, aes(bin, Frequency, color=Frequency)) + geom_bar(stat="identity", position="stack")

FYI: This is more of an extended comment than an answer.

To me, this new plot looks like a stacked bar where each bar's height is equal to the intersection points of the upper and lower line at the next trial.

enter image description here

The way that I would approach this is to treat "Trials" as a categorical variable. Then we can search each row of xcum for elements that are equal. If they are, then we can consider this to be a point of intersection whose minima also represents the multiple defining the height of our bars.

x <- t(xcum)
x <- x[duplicated(x),]
x[x==0] <- NA

Now we have the multiples of the actual points, we need to figure out how to take it to the next step and find a way of binning the information. That means we need to make a decision about how many points will represent each grouping. Let's write some points out for posterity.

Trial 1 (2) = 1, 0.5 # multiple = 0.5
Trial 2 (3) = 1, 0.66, 0.33 #  multiple = 0.33
Trial 3 (4) = 1, 0.75, 0.5, 0.25 # multiple = 0.25
Trial 4 (5) = 1, 0.8,  0.6, 0.4, 0.2 # multiple = 0.2
Trial 5 (6) = 1, 0.8333335, 0.6666668, 0.5000001, 0.3333334, 0.1666667
... 
Trial 36 (35) = 1, 0.9722223, ..., 0.02777778 # mutiple = 0.05555556 / 2

In other words, for each Trial there are n-1 points to plot. In your drawing you have 7 bins. So we need to figure out the multiples for each bin.

Let's cheat and divide the last two columns by two, we know from visual inspection that the minima is lower than 0.05

x[,35:36] <- x[,35:36] / 2

Then find the minimum of each column:

x <- apply(x, 2, function(x) min(x, na.rm=T))[-1] # Drop the 1
x <- x[c(1,2,3,4,8,17,35)] # I'm just guessing here by the "look" of your drawing.

The clearest way to do this is to create each bin separately. Obviously, this could be done automatically later. Remembering that each point is

bin1 <- data.frame(bin = rep("bin1",2), Frequency = rep(x[1],2))
bin2 <- data.frame(bin = rep("bin2",3), Frequency = rep(x[2],3))
bin3 <- data.frame(bin = rep("bin3",4), Frequency = rep(x[3],4))
bin4 <- data.frame(bin = rep("bin4",5), Frequency = rep(x[4],5))
bin5 <- data.frame(bin = rep("bin5",9), Frequency = rep(x[5],9))
bin6 <- data.frame(bin = rep("bin6",18), Frequency = rep(x[6],18))
bin7 <- data.frame(bin = rep("bin7",36), Frequency = rep(x[7],36))

df <- rbind(bin1,bin2,bin3,bin4,bin5,bin6,bin7)
ggplot(df, aes(bin, Frequency, color=Frequency)) + geom_bar(stat="identity", position="stack")

回复收藏 0 原文

~没有更多了~