绘制加权频率矩阵

Question

这个问题与我之前问过的两个不同问题有关：

1）再现频率矩阵图

2 ) 向累积图添加 95% 置信限

I希望在 R 中重现此图：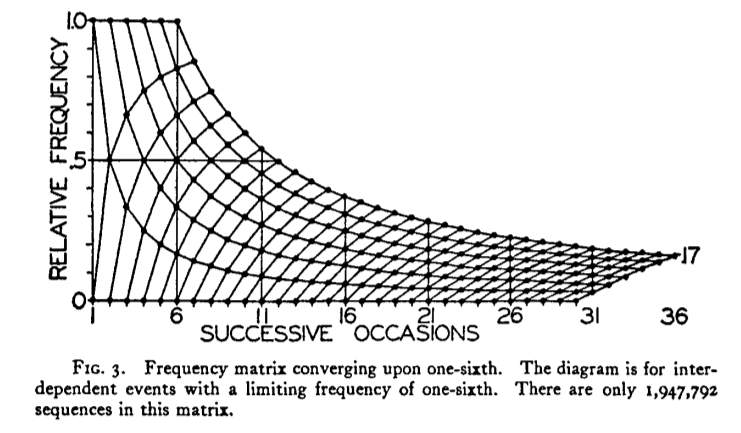

我已经使用图形下面的代码：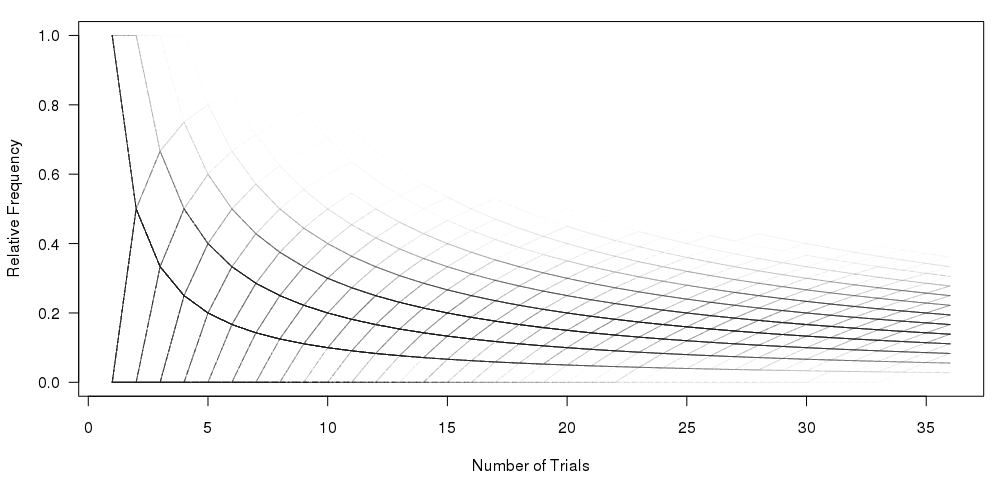

#Set the number of bets and number of trials and % lines
numbet <- 36 
numtri <- 1000 
#Fill a matrix where the rows are the cumulative bets and the columns are the trials
xcum <- matrix(NA, nrow=numbet, ncol=numtri)
for (i in 1:numtri) {
x <- sample(c(0,1), numbet, prob=c(5/6,1/6), replace = TRUE)
xcum[,i] <- cumsum(x)/(1:numbet)
}
#Plot the trials as transparent lines so you can see the build up
matplot(xcum, type="l", xlab="Number of Trials", ylab="Relative Frequency", main="", col=rgb(0.01, 0.01, 0.01, 0.02), las=1)

我的问题是：如何在不绘制多个样本的情况下一次性重现顶部图？

谢谢。

Answer 1

生成此图...

...

您可以使用以下代码

boring <- function(x, occ) occ/x

boring_seq <- function(occ, length.out){
  x <- seq(occ, length.out=length.out)
  data.frame(x = x, y = boring(x, occ))
}

numbet <- 31
odds <- 6
plot(1, 0, type="n",  
    xlim=c(1, numbet + odds), ylim=c(0, 1),
    yaxp=c(0,1,2),
    main="Frequency matrix", 
    xlab="Successive occasions",
    ylab="Relative frequency"
    )

axis(2, at=c(0, 0.5, 1))    

for(i in 1:odds){
  xy <- boring_seq(i, numbet+1)
  lines(xy$x, xy$y, type="o", cex=0.5)
}

for(i in 1:numbet){
  xy <- boring_seq(i, odds+1)
  lines(xy$x, 1-xy$y, type="o", cex=0.5)
}

Answer 2

您还可以使用 Koshke 的方法，通过将值的组合限制为 s<6 的值，并根据 Andrie 的要求添加 Ps$n 和 ps$s 差异的条件，以获得“指向的”配置。

 ps <- ldply(0:35, function(i)data.frame(s=0:i, n=i))
 plot.new()
 plot.window(c(0,36), c(0,1))
 apply(ps[ps$s<6 & ps$n - ps$s < 30, ], 1, function(x){
   s<-x[1]; n<-x[2];
   lines(c(n, n+1, n, n+1), c(s/n, s/(n+1), s/n, (s+1)/(n+1)), type="o")})
 axis(1)
 axis(2)
 lines(6:36, 6/(6:36), type="o")
 # need to fill in the unconnected points on the upper frontier

Answer 3

加权频率矩阵也称为位置权重矩阵（生物信息学）。
它可以以序列徽标的形式表示。
这至少是我绘制加权频率矩阵的方式。

library(cosmo)
data(motifPWM); attributes(motifPWM) # Loads a sample position weight matrix (PWM) containing 8 positions.
plot(motifPWM) # Plots the PWM as sequence logo.