获取给定当前点、距离和方位的纬度/经度
给定现有的纬度/经度点、距离(以公里为单位)和方位角(以度数转换为弧度),我想计算新的纬度/经度。 这个网站一遍又一遍地出现,但我就是做不到得到适合我的公式。
上述链接中的公式为:
lat2 = asin(sin(lat1)*cos(d/R) + cos(lat1)*sin(d/R)*cos(θ))
lon2 = lon1 + atan2(sin(θ)*sin(d/R)*cos(lat1), cos(d/R)−sin(lat1)*sin(lat2))
上面的公式适用于 MSExcel,其中 -
asin = arc sin()
d = distance (in any unit)
R = Radius of the earth (in the same unit as above)
and hence d/r = is the angular distance (in radians)
atan2(a,b) = arc tan(b/a)
θ is the bearing (in radians, clockwise from north);
这是我在 Python 中得到的代码。
import math
R = 6378.1 #Radius of the Earth
brng = 1.57 #Bearing is 90 degrees converted to radians.
d = 15 #Distance in km
#lat2 52.20444 - the lat result I'm hoping for
#lon2 0.36056 - the long result I'm hoping for.
lat1 = 52.20472 * (math.pi * 180) #Current lat point converted to radians
lon1 = 0.14056 * (math.pi * 180) #Current long point converted to radians
lat2 = math.asin( math.sin(lat1)*math.cos(d/R) +
math.cos(lat1)*math.sin(d/R)*math.cos(brng))
lon2 = lon1 + math.atan2(math.sin(brng)*math.sin(d/R)*math.cos(lat1),
math.cos(d/R)-math.sin(lat1)*math.sin(lat2))
print(lat2)
print(lon2)
我明白了
lat2 = 0.472492248844
lon2 = 79.4821662373
Given an existing point in lat/long, distance in (in KM) and bearing (in degrees converted to radians), I would like to calculate the new lat/long. This site crops up over and over again, but I just can't get the formula to work for me.
The formulas as taken the above link are:
lat2 = asin(sin(lat1)*cos(d/R) + cos(lat1)*sin(d/R)*cos(θ))
lon2 = lon1 + atan2(sin(θ)*sin(d/R)*cos(lat1), cos(d/R)−sin(lat1)*sin(lat2))
The above formula is for MSExcel where-
asin = arc sin()
d = distance (in any unit)
R = Radius of the earth (in the same unit as above)
and hence d/r = is the angular distance (in radians)
atan2(a,b) = arc tan(b/a)
θ is the bearing (in radians, clockwise from north);
Here's the code I've got in Python.
import math
R = 6378.1 #Radius of the Earth
brng = 1.57 #Bearing is 90 degrees converted to radians.
d = 15 #Distance in km
#lat2 52.20444 - the lat result I'm hoping for
#lon2 0.36056 - the long result I'm hoping for.
lat1 = 52.20472 * (math.pi * 180) #Current lat point converted to radians
lon1 = 0.14056 * (math.pi * 180) #Current long point converted to radians
lat2 = math.asin( math.sin(lat1)*math.cos(d/R) +
math.cos(lat1)*math.sin(d/R)*math.cos(brng))
lon2 = lon1 + math.atan2(math.sin(brng)*math.sin(d/R)*math.cos(lat1),
math.cos(d/R)-math.sin(lat1)*math.sin(lat2))
print(lat2)
print(lon2)
I get
lat2 = 0.472492248844
lon2 = 79.4821662373
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(15)
对于对 Java 解决方案感兴趣的人,这里是我的代码:
我注意到最初的解决方案需要一些调整才能返回正确的经度值,特别是当该点位于其中一个极点时。
有时还需要进行舍入操作,因为 0 纬度/经度的结果似乎稍微偏离 0。对于小距离,舍入将在这方面有所帮助。
For whoever is interested in a Java solution here is my code:
I noticed that the initial solution needs some tweaks in order to return a proper longitude value, especially when the point is at one of the poles.
Also a round operation is sometimes required as the results on 0 latitude / longitude seem to slightly shift away from 0. For small distances, rounding will help in this regard.
聚会已经很晚了,但这里有 R 语言的答案,供任何感兴趣的人参考。我所做的唯一更改是将半径设置为米,因此 d 也需要设置为米。
Very late to the party, but here is answer in R for anyone interested. Only change I've made is that I've set the radius to metres, so
dneeds to be set to meters too.需要将答案从弧度转换回角度。工作代码如下:
Needed to convert answers from radians back to degrees. Working code below:
geopy 库支持此功能:
通过 https://stackoverflow.com/a/4531227/37610
The geopy library supports this:
Found via https://stackoverflow.com/a/4531227/37610
这个问题在大地测量学研究中被称为直接问题。
这确实是一个非常受欢迎的问题,也是一个经常引起混乱的问题。原因是大多数人都在寻找简单直接的答案。但没有,因为大多数问这个问题的人没有提供足够的信息,仅仅是因为他们没有意识到:
R。请参阅此处。因此,根据您所需的精度,各种几何模型中使用了许多不同的假设,这些假设的应用也不同。因此,要回答这个问题,您需要考虑您希望得到的结果的准确性。
一些示例:
纬度中寻找小距离(<100公里)的最近几公里的大致位置0-70 度N|S 之间。 (地球是~平坦模型。)所以你可以有多种选择来使用哪种算法。此外,每种编程语言都有自己的实现或“包”乘以模型数量和模型开发人员的特定需求。出于所有实际目的,忽略
javascript之外的任何其他语言都是值得的,因为它本质上非常类似于伪代码。因此,它可以轻松地转换为任何其他语言,只需进行最小的更改。主要模型有:
欧几里得/地平模型:适用于~10公里以下的极短距离球形模型:适用于较大的纵向距离,但纬度差异较小。热门型号:椭圆体模型:在任何纬度/经度和距离上最准确,但仍然是数值近似值,具体取决于您需要的精度。一些流行的型号是:参考文献:
This question is known as the direct problem in the study of geodesy.
This is indeed a very popular question and one that is a constant cause of confusion. The reason is that most people are looking for a simple and straight-forward answer. But there is none, because most people asking this question are not supplying enough information, simply because they are not aware that:
R. See here.Therefore there are many different assumptions used in the various geometric models that apply differently, depending on your needed accuracy. So to answer the question you need to consider to what accuracy you would like to have your result.
Some examples:
latitudesbetween0-70 degN|S. (Earth is ~flat model.)nanometers[nm].So you can have many choices in which algorithm to use. In addition each programming language has it's own implementation or "package" multiplied by number of models and the model developers specific needs. For all practical purposes here, it pays off to ignore any other language apart
javascript, since it very closely resemble pseudo-code by its nature. Thus it can be easily converted to any other language, with minimal changes.Then the main models are:
Euclidian/Flat earth model: good for very short distances under ~10 kmSpherical model: good for large longitudinal distances, but with small latitudinal difference. Popular model:Ellipsoidal models: Most accurate at any lat/lon and distance, but is still a numerical approximation that depend on what accuracy you need. Some popular models are:References:
回答可能有点晚了,但在测试其他答案后,它们似乎无法正常工作。这是我们在系统中使用的 PHP 代码。全方位开展工作。
PHP代码:
May be a bit late for answering, but after testing the other answers, it appears they don't work correctly. Here is a PHP code we use for our system. Working in all directions.
PHP code:
我将 Brad 的答案移植到普通 JS 答案,没有 Bing 地图依赖
https://jsfiddle.net/kodisha/8a3hcjtd /
此外,我添加了
geoJSON导出,因此您只需将生成的 geoJSON 粘贴到:http://geojson.io/#map=17/41.89017/12.49171< /a> 立即查看结果。结果:
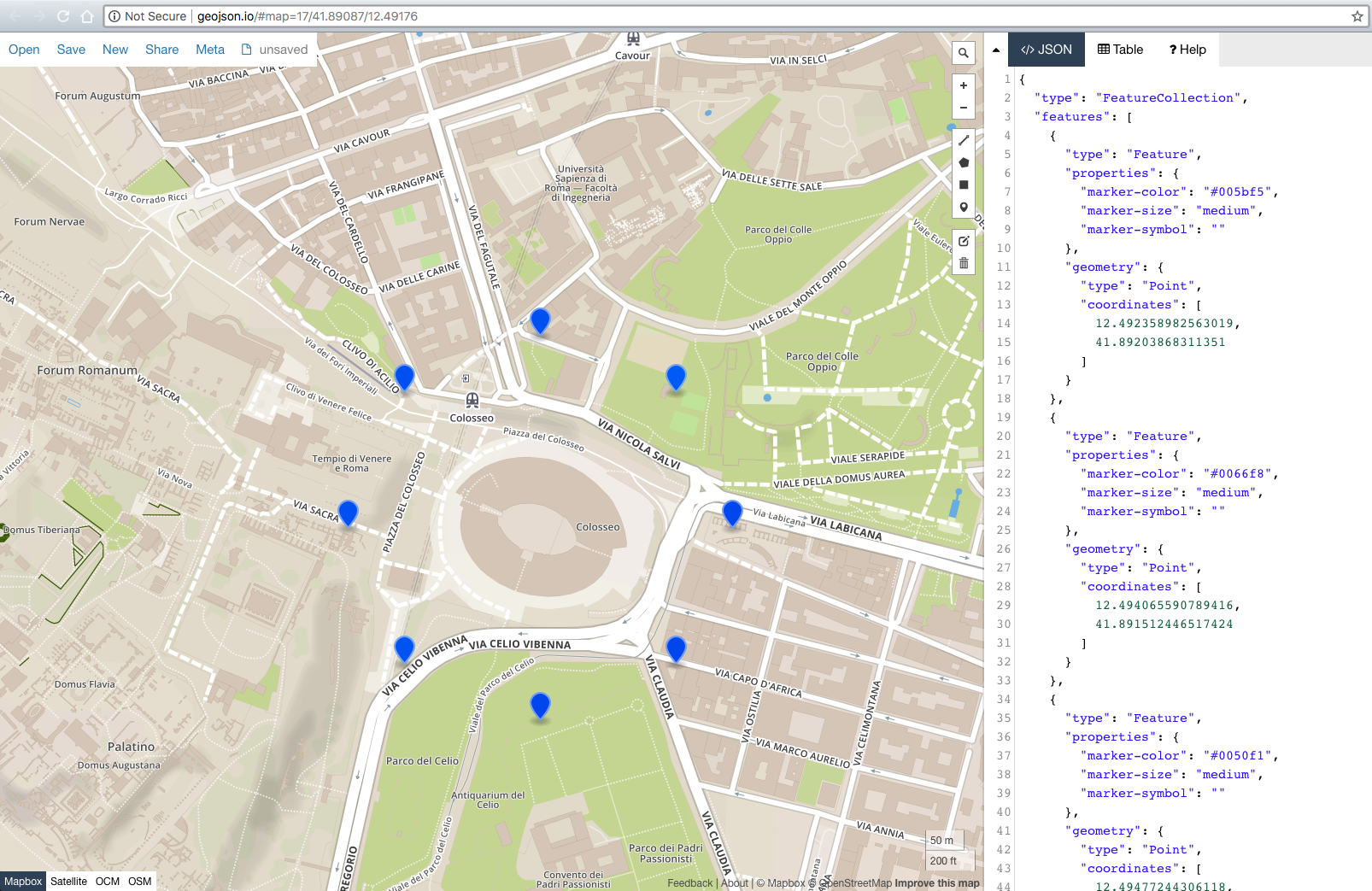
I ported answer by Brad to vanilla JS answer, with no Bing maps dependency
https://jsfiddle.net/kodisha/8a3hcjtd/
In addition, I added
geoJSONexport, so you can simply paste resulting geoJSON to:http://geojson.io/#map=17/41.89017/12.49171to see the results instantly.Result:

使用 geopy 的快速方法
Quick way using geopy
lon1 和 lat1(以度为单位)
brng = 方位角(以弧度为单位
) d = 距离(以公里为单位)
R = 地球半径(以公里为单位)
我在 PHP 中实现了您的算法和我的算法并对其进行了基准测试。这个版本的运行时间约为 50%。生成的结果是相同的,因此在数学上似乎是等效的。
我没有测试上面的 python 代码,因此可能存在语法错误。
lon1 and lat1 in degrees
brng = bearing in radians
d = distance in km
R = radius of the Earth in km
I implemented your algorithm and mine in PHP and benchmarked it. This version ran in about 50% of the time. The results generated were identical, so it seems to be mathematically equivalent.
I didn't test the python code above so there might be syntax errors.
我将 Python 移植到了 Javascript。这将返回一个 Bing Maps
Location对象,您可以更改为您喜欢的任何内容。I ported the Python to Javascript. This returns a Bing Maps
Locationobject, you can change to whatever you like.感谢@kodisha,这是一个 Swift 版本,但对地球半径的计算进行了改进和更精确:
Thanks to @kodisha, here is a Swift version, but with improved and more precise calculation for Earth radius:
虽然也晚了,但对于那些可能发现这一点的人来说,您将使用 geographiclib 库获得更准确的结果。查看测地线问题描述和 JavaScript 示例,轻松介绍如何使用它来回答主题问题以及许多其他问题。以包括 Python 在内的多种语言实现。如果您关心准确性,这比您自己编写代码要好得多;比早期“使用库”推荐中的 VincentyDistance 更好。正如文档所述:“重点是返回准确的结果,误差接近四舍五入(约 5-15 纳米)。”
Also late but for those who might find this, you will get more accurate results using the geographiclib library. Check out the geodesic problem descriptions and the JavaScript examples for an easy introduction to how to use to answer the subject question as well as many others. Implementations in a variety of languages including Python. Far better than coding your own if you care about accuracy; better than VincentyDistance in the earlier "use a library" recommendation. As the documentation says: "The emphasis is on returning accurate results with errors close to round-off (about 5–15 nanometers)."
只需交换 atan2(y,x) 函数中的值即可。不是 atan2(x,y)!
Just interchange the values in the atan2(y,x) function. Not atan2(x,y)!
如果有人想要这个,我将答案从@David M移植到java...我确实得到了略有不同的结果 52.20462299620793, 0.360433887489931
I ported the answer from @David M to java if anyone wanted this... I do get a slight different result of 52.20462299620793, 0.360433887489931
这是基于 Ed Williams Aviation Formulary 的 PHP 版本。 PHP 中模数的处理方式略有不同。这对我有用。
Here is a PHP version based on Ed Williams Aviation Formulary. Modulus is handled a little different in PHP. This works for me.