“来自不同的顶点链”是什么意思？在这个最近邻算法中？

Question

以下伪代码来自算法设计手册在线预览版的第一章（第7页来自此 PDF）。

这个例子是一个有缺陷的算法，但我仍然很想理解它：

[...] 一个不同的想法可能是重复连接最近的一对 连接不会产生问题的端点，例如 周期提前终止。每个顶点都有自己的开始 单顶点链。将所有内容合并在一起后，我们最终会 包含其中所有点的单个链。连接 最后两个端点给了我们一个循环。执行过程中的任意一步 对于这个最近对启发式，我们将有一组单个顶点 和可合并的顶点不相交链。在伪代码中：

ClosestPair(P)
    Let n be the number of points in set P.
    For i = 1  to n − 1 do
        d = ∞
        For each pair of endpoints (s, t) from distinct vertex chains
            if dist(s, t) ≤ d then sm = s, tm = t, and d = dist(s, t)
        Connect (sm, tm) by an edge
    Connect the two endpoints by an edge

请注意 sm 和 tm 应该是 sm 和 <代码>t_m。

首先，我不明白“来自不同的顶点链”是什么意思。其次，i 在外循环中用作计数器，但 i 本身从未在任何地方实际使用过！有比我聪明的人可以解释一下这里到底发生了什么吗？

Answer 1

在欧内斯特·弗里德曼-希尔（Ernest Friedman-Hill）的解释（已接受的答案）之后，我是这样看的：

所以来自同一本书的例子（图1.4）。
我已向顶点添加了名称以使其清晰

所以第一步所有顶点都是单顶点链，所以我们连接 AD、BE 和 CF 对，b/ c 之间的距离最小。

在第二步中，我们有 3 条链，AD 和 BE 之间的距离与 BE 和 CF 之间的距离相同，因此我们将 AD 与 BE 连接起来，我们留下两条链 - ADEB 和 CF

在第三步中，有唯一的方法连接它们是通过 B 和 C，b/c BC 比 BF、AF 和 AC 短（记住我们只考虑链的端点）。所以我们现在有一条链 ADEBCF。

在最后一步，我们连接两个端点（A 和 F）以获得一个循环。

Answer 2

1）描述指出每个顶点总是要么属于“单顶点链”（即，它是单独的），要么属于另一个链；一个顶点只能属于一条链。该算法表示，在每一步中，您都会选择每对可能的两个顶点，这两个顶点都是它们所属的各自链的端点，并且尚未属于同一链。有时他们会是单身；有时他们会单身。有时，其中一个或两个已经属于一个重要的链，因此您将加入两个链。

2) 重复循环n次，以便最终选择每个顶点；但是，是的，实际的迭代计数没有用于任何用途。重要的是你运行循环的次数足够多。

Answer 3

虽然问题已经得到解答，但这里有一个最近对启发式的 python 实现。它从每个点作为一条链开始，然后连续扩展链以构建一条包含所有点的长链。
该算法确实构建了一条路径，但它不是机器人手臂运动的序列，因为手臂起点未知。

import matplotlib.pyplot as plot
import math
import random


def draw_arrow(axis, p1, p2, rad):
    """draw an arrow connecting point 1 to point 2"""
    axis.annotate("",
              xy=p2,
              xytext=p1,
              arrowprops=dict(arrowstyle="-", linewidth=0.8, connectionstyle="arc3,rad=" + str(rad)),)


def closest_pair(points):
    distance = lambda c1p, c2p:  math.hypot(c1p[0] - c2p[0], c1p[1] - c2p[1])
    chains = [[points[i]] for i in range(len(points))]
    edges = []
    for i in range(len(points)-1):
        dmin = float("inf")  # infinitely big distance
        # test each chain against each other chain
        for chain1 in chains:
            for chain2 in [item for item in chains if item is not chain1]:
                # test each chain1 endpoint against each of chain2 endpoints
                for c1ind in [0, len(chain1) - 1]:
                    for c2ind in [0, len(chain2) - 1]:
                        dist = distance(chain1[c1ind], chain2[c2ind])
                        if dist < dmin:
                            dmin = dist
                            # remember endpoints as closest pair
                            chain2link1, chain2link2 = chain1, chain2
                            point1, point2 = chain1[c1ind], chain2[c2ind]
        # connect two closest points
        edges.append((point1, point2))
        chains.remove(chain2link1)
        chains.remove(chain2link2)
        if len(chain2link1) > 1:
            chain2link1.remove(point1)
        if len(chain2link2) > 1:
            chain2link2.remove(point2)
        linkedchain = chain2link1
        linkedchain.extend(chain2link2)
        chains.append(linkedchain)
    # connect first endpoint to the last one
    edges.append((chains[0][0], chains[0][len(chains[0])-1]))
    return edges


data = [(0.3, 0.2), (0.3, 0.4), (0.501, 0.4), (0.501, 0.2), (0.702, 0.4), (0.702, 0.2)]
# random.seed()
# data = [(random.uniform(0.01, 0.99), 0.2) for i in range(60)]
edges = closest_pair(data)
# draw path
figure = plot.figure()
axis = figure.add_subplot(111)
plot.scatter([i[0] for i in data], [i[1] for i in data])
nedges = len(edges)
for i in range(nedges - 1):
    draw_arrow(axis, edges[i][0], edges[i][1], 0)
# draw last - curved - edge
draw_arrow(axis, edges[nedges-1][0], edges[nedges-1][1], 0.3)
plot.show()

Answer 4

TLDR：如果已经熟悉本线程中提出的问题以及迄今为止提供的答案，请跳至下面的“ClestPair 启发式的澄清描述”部分。

备注：我最近开始学习算法设计手册，ClosestPair启发式示例让我感到困扰，因为我觉得它缺乏清晰度。看来其他人也有类似的感受。不幸的是，这个帖子上提供的答案并没有完全适合我——我觉得它们对我来说都有点太模糊了。但这些答案确实帮助我朝着我认为对斯基纳的正确解释的方向前进。

问题陈述和背景：来自本书第 5 页，供那些没有该书的人参考（第 3 版）：

Skiena 首先详细介绍了如何NearestNeighbor 启发式是不正确的，使用下图来帮助说明他的情况：

上图说明了NearestNeighbor 启发式，底部的数字是最优解。显然，需要采用不同的方法来找到最佳解决方案。提示 ClosestPair 启发式以及此问题的原因。

书籍描述：书中概述了 ClosestPair 启发式的以下描述：

也许我们需要的是针对最近邻启发式的坏实例的实例采取不同的方法。总是走到最近的点限制太大，因为这似乎会让我们做出我们不想要的动作。

不同的想法可能会重复连接最接近的端点对，这些端点的连接不会产生问题，例如循环的提前终止。每个顶点都以其自己的单个顶点链开始。将所有内容合并在一起后，我们最终将得到一条包含其中所有点的链。连接最后两个端点给我们一个循环。在执行此最近对启发式过程中的任何步骤，我们都会有一组单个顶点和可用于合并的顶点不相交链的末尾。实现此描述的伪代码如下所示。

---

ClosestPair 启发式的澄清描述

首先“放大”一点并回答我们正在尝试寻找什么的基本问题可能会有所帮助用图论术语：

最短的闭合路径是什么？

也就是说，我们想要找到一系列边 (e_1, e_2, ..., e_{n-1}) ，其中存在一系列顶点 (v_1, v_2, ..., v_n) 其中 v_1 = v_n 并且所有边都是不同的。边是加权的，其中每条边的权重只是构成该边的顶点之间的距离——我们希望最小化存在的任何闭合路径的总权重。

实际上，ClosestPair 启发式为伪代码中外部 for 循环的每次迭代提供了这些不同的边之一（行 3-10），其中内部 for 循环（第 5-9 行）确保在每个步骤中选择不同的边缘，(s_m, t_m)，是由来自不同顶点链端点的顶点组成；也就是说，s_m 来自一个顶点链的端点，而 t_m 来自另一个不同顶点链的端点。内部 for 循环只是确保我们考虑所有这些对，从而最小化过程中潜在顶点之间的距离。

注意（顶点之间距离的关系）：一个潜在的混乱来源是在两个 for 循环中都没有指定任何“处理顺序”。我们如何确定比较端点以及这些端点的顶点的顺序？没关系。内部 for 循环的性质清楚地表明，在存在联系的情况下，将选择最近遇到的具有最小距离的顶点对。

ClosestPair 启发式的好实例

回想一下应用 NearestNeighbor 启发式的坏实例中发生的情况（观察新添加的顶点标签）：

总距离很荒谬，因为我们一直在 0 上来回跳跃。

现在考虑一下当我们使用 ClosestPair 启发式时会发生什么。我们有 n = 7 个顶点；因此，伪代码表明外部 for 循环将执行 6 次。正如书中所指出的，每个顶点都以它自己的单个顶点链开始（即，每个点都是一个单例，其中单例是一条具有一个端点的链）。在我们的例子中，根据上图，内部 for 循环将执行多少次？那么，有多少种方法可以选择 n 元素集的 2 元素子集（即 2 元素子集代表潜在的顶点配对）？有 n 选择 2 这样的子集：

因为 n = 7 在我们的例子中，总共有 21 个可能的顶点配对需要研究。上图的性质清楚地表明，(C, D) 和 (D, E) 是第一次迭代的唯一可能结果，因为它们之间的最小可能距离开头的顶点为 1，并且 dist(C, D) = dist(D, E) = 1。由于没有处理顺序，因此尚不清楚实际上连接哪些顶点来给出第一条边 (C, D) 或 (D, E)。假设我们最后遇到顶点 D 和 E，从而导致 (D, E) 作为我们的第一条边。

现在还有 5 次迭代需要进行，并且需要考虑 6 个顶点链：A、B、C、(D、E)、F、G。

注意（每次迭代都会消除一个顶点链）：ClosestPair 启发式中的外部 for 循环的每次迭代都会导致消除一个顶点链。外部 for 循环迭代继续，直到留下由所有顶点组成的单个顶点链，其中最后一步是通过边连接该单个顶点链的两个端点。更准确地说，对于由 n 个顶点组成的图 G，我们从 n 个顶点链开始（即，每个顶点作为其自己的单个顶点开始）链）。外部 for 循环的每次迭代都会导致连接 G 的两个顶点，这些顶点来自不同的顶点链；也就是说，连接这些顶点会导致将两个不同的顶点链合并为一个，从而使剩下要考虑的顶点链总数减1。对于具有 n 个顶点的图重复此过程 n - 1 次会导致留下 n - (n - 1) = 1顶点链，包含 G 中所有点的单链。连接最后两个端点给我们一个循环。

每次迭代的一种可能的描述如下：

ClosestPair outer for loop iterations
  1: connect D to E # -> dist: 1, chains left (6): A, B, C, (D, E), F, G
  2: connect D to C # -> dist: 1, chains left (5): A, B, (C, D, E), F, G
  3: connect E to F # -> dist: 3, chains left (4): A, B, (C, D, E, F), G
  4: connect C to B # -> dist: 4, chains left (3): A, (B, C, D, E, F), G
  5: connect F to G # -> dist: 8, chains left (2): A, (B, C, D, E, F, G)
  6: connect B to A # -> dist: 16, single chain: (A, B, C, D, E, F, G)

Final step: connect A and G

因此，在本示例中，ClosestPair 启发式做了正确的事情，而之前 NearestNeighbor 启发式做了错误的事情：

ClosestPair 启发式的错误实例

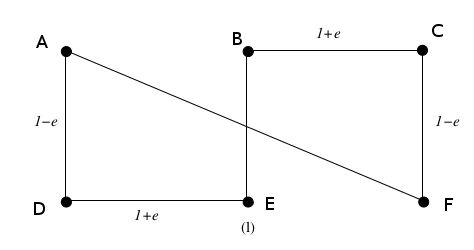
考虑 ClosestPair 算法对下图中的点集执行的操作（首先尝试想象一下可能会有所帮助）没有任何边连接顶点的点集）：

我们如何使用 ClosestPair 连接顶点？我们有 n = 6 个顶点；因此，外部 for 循环将执行 6 - 1 = 5 次，其中我们的首要任务是调查

所有可能对的顶点之间的距离。上图帮助我们看到 dist(A, D) = dist(B, E) = dist(C, F) = 1 - ɛ 是自 以来第一次迭代中唯一可能的选项>1 - ɛ 是任意两个顶点之间的最短距离。我们任意选择(A, D)作为第一个配对。

现在还有 4 次迭代需要进行，并且需要考虑 5 个顶点链：(A, D)、B、C、E、F。每次迭代的一种可能的描述如下：

ClosestPair outer for loop iterations
  1: connect A to D # --> dist: 1-ɛ, chains left (5): (A, D), B, C, E, F
  2: connect B to E # --> dist: 1-ɛ, chains left (4): (A, D), (B, E), C, F
  3: connect C to F # --> dist: 1-ɛ, chains left (3): (A, D), (B, E), (C, F)
  4: connect D to E # --> dist: 1+ɛ, chains left (2): (A, D, E, B), (C, F)
  5: connect B to C # --> dist: 1+ɛ, single chain: (A, D, E, B, C, F)

Final step: connect A and F

注意（正确考虑从不同顶点链连接的端点）：上面描述的迭代1-3在我们没有其他有意义的选择可以考虑。即使我们有了不同的顶点链 (A, D)、(B, E) 和 (C, F)，下一个选择同样是平淡无奇且随意的。鉴于第四次迭代中顶点之间的最小可能距离为 1 + ɛ，有四种可能性：(A, B), (D, E), (B, C), ( E，F）。上述所有点的顶点之间的距离为 1 + ɛ。 (D, E) 的选择是任意的。其他三个顶点配对中的任何一个都可以发挥同样的作用。但请注意迭代5期间发生的情况——我们对顶点配对的可能选择已经被严格缩小。具体来说，顶点链 (A, D, E, B) 和 (C, F) 具有端点 (A, B)和 (C, F) 分别只允许四种可能的顶点配对：(A, C)、(A, F)、(B, C)、(B, F) 。即使这看起来很明显，但值得注意的是，D 和 E 都不是上面可行的候选顶点——这两个顶点都不包含在端点中，( A, B)，它们为顶点的顶点链，即(A, D, E, B)。现阶段没有任意选择。上面对中的顶点之间的距离没有联系。 (B, C) 配对产生顶点之间的最小距离：1 + ɛ。一旦顶点 B 和 C 通过边连接起来，所有迭代都已完成，我们只剩下一个顶点链：(A, D, E ，B，C，F）。连接A和F给我们一个循环并结束这个过程。

穿过 (A, D, E, B, C, F) 的总距离如下：

上面的距离计算为 5 - ɛ + √(5ɛ^2 + 6ɛ + 5 )，而不是仅绕边界行驶的总距离（上图中右侧的图，所有边缘都涂成红色）：6 + 2ɛ。作为 ɛ -> 0，我们看到5 + √5 ≈ 7.24 > 6 其中 6 是必要的行程量。 我们最终会走得比需要的更远。

因此，在这种情况下，通过使用 ClosestPair 启发式，