寻找曲线最平滑的 15%
找到类似于下面的曲线的最平滑 15% 的最佳方法是什么?
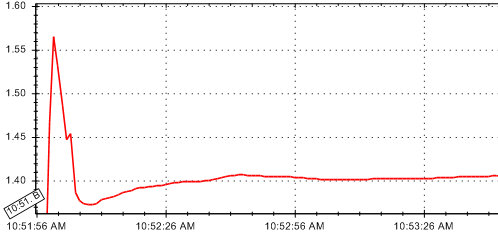
我需要知道开始和结束的 x 坐标。我考虑过使用导数函数,但这会给我一个具有最小导数的点,它可能或可能不总是最平滑的 15% 的一部分。
我应该看什么算法或建议?
What would be the best way to find the smoothest 15% of a curve similar to the one below?

I need to know the beginning and ending x coordinates. I have thought about using a derivative function, but this will give me a point with the smallest derivative, which may or may not always be part of the smoothest 15%.
Any algorithms I should look at or suggestions?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
除非今天我对计算的记忆比平常更糟糕,否则你想要的是二阶导数。
或者,您可以使用正确大小的滑动窗口,并计算每个位置的窗口的方差,方差最小的应该是最平滑的。
当然,这也要看你如何定义“流畅”。您的意思是 Y 值的最小变化,还是(例如)几乎完全直线(但也几乎垂直)的线至少符合“平滑”的条件?
Unless my memory of calc fails me even more than usual today, what you'd want here would be the second derivative.
Alternatively, you could just use a sliding window of the correct size, and compute the variance for the window at each position, and the one with the smallest variance should be the smoothest.
Of course, it also depends on how you define "smooth". Do you mean the smallest change in the Y value, or would (for example) the almost perfectly straight (but also nearly vertical) line at the lest qualify as "smooth"?
我将决定分析的分辨率(即闭区间的大小,称为 delta X),然后正如 @Jerry 提到的,找到该闭区间内函数的最大值和最小值,包括端点。
这将为您提供 n 个间隔(或增量 Xs),并且您将找到每个间隔的最大值和最小值(我们将其称为增量 Ys)。
现在,您基本上已经将函数的域分割为那些 n 个 delta X,每个 delta X 都有一个相应的 delta Y。
然后您应该能够对间隔进行分组,以便一组 m em> 区间加起来达到函数域的 15%。我们将一组 m 间隔称为分析的“窗口大小”。
看来您应该能够在单个增量 X 的宽度上滑动窗口,并对窗口的增量 Y 求和。存储该值,然后滑过另一个增量 X,直到空间不足(同时在域中保留整个窗口大小)。找到最小的总和,它应该对应于“最平滑”的 15%——假设平滑意味着 Y 方差最小。
I would decide on a resolution for the analysis (i.e. the size of your closed interval, call it delta X), and then as @Jerry mentioned, find the max and min of the function within that closed interval, including the end points.
That will give you n intervals (or delta Xs), and you will have found the max and min of each interval (let's call them the delta Ys).
Now you will essentially have cut up your function's domain into those n delta Xs, each having a corresponding delta Y.
You should then be able to group the intervals so that a group of m intervals adds up to 15% of the function domain. Let's call a group of m intervals your "window size" of analysis.
It seems like then you should be able to slide the window over the width of a single delta X, and sum the delta Ys for the window. Store that value, and then slide over another delta X, until you run out of space (while keeping a whole window size in the domain). Find the smallest sum, and that should correspond to the "smoothest" 15%-- given that smooth means least Y variance.