混合两个函数,其中一个函数是反函数
让我首先解释一下这个想法。实际的数学问题在屏幕截图下方。 出于音乐目的,我正在构建一种律动算法,其中事件位置由数学函数 F(X) 转换。位置在凹槽范围内标准化,因此我基本上处理 0 到 1 之间的值(这使得塑造凹槽曲线更容易 - 唯一的限制是 x'>=0)。 该凹槽算法接受任何事件位置,并且还通过从时间线音符轨道等数据结构中过滤静态音符来工作。为了过滤特定范围(音频块大小)内的事件,我需要逆凹槽函数来定位轨道中的音符并将它们转换到凹槽空间。到目前为止,一切都很好。有用!
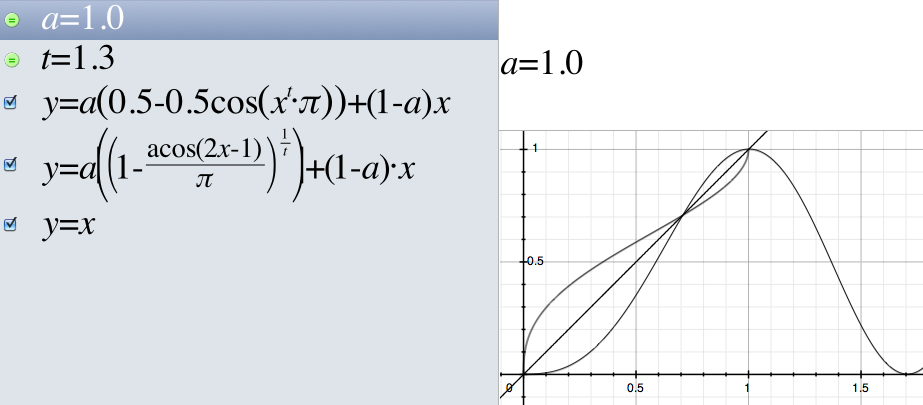
因为它镜像到 (y=x)。所以我可以插入一个值 x 并得到一个 y。显然,这个 y 可以代入反函数来再次得到第一个 x。
问题:我现在希望能够将凹槽混合到另一个凹槽中,但是通常的线性(提示提示)混合代码的行为并不像我预期的那样。为了使它更容易,我首先尝试混合到 y=x。
B(x)=alpha*F(x) + (1-alpha)*x;
iB(x)=alpha*iF(x) + (1-alpha)*x;
当 alpha=1 时,我们得到完整的曲线。当 alpha=0 时,我们得到直线。但对于 0 到 1 之间的 alpha,B(x) 和 iB(x) 不再镜像(接近,但不够),F(x) 和 iF(x) 仍然镜像。
有没有解决方案(除了将曲线量化为线段之外)?有什么我应该关注的主题吗?
Let me first explain the idea. The actual math question is below the screenshots.
For musical purpose I am building a groove algorithm where event positions are translated by a mathematical function F(X). The positions are normalized inside the groove range, so I am basically dealing with values between zero and one (which makes shaping groove curves way easier-the only limitation is x'>=0).
This groove algorithm accepts any event position and also work by filtering static notes from a data-structure like a timeline note-track. For filtering events in a certain range (audio block-size) I need the inverse groove-function to locate the notes in the track and transform them into the groove space. So far so good. It works!
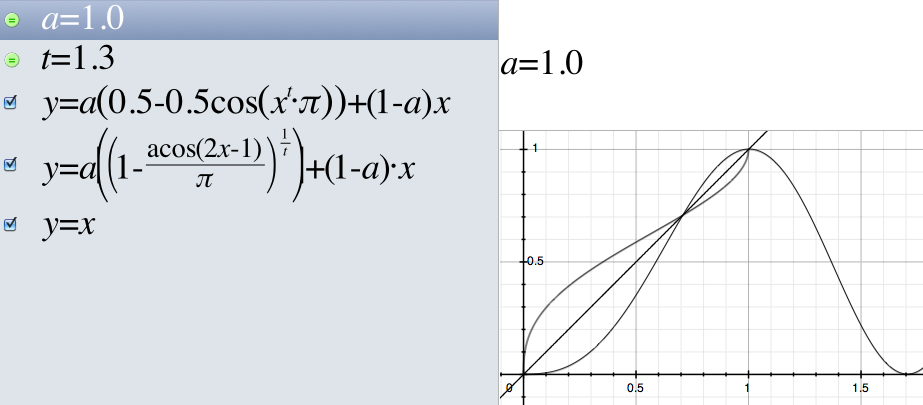
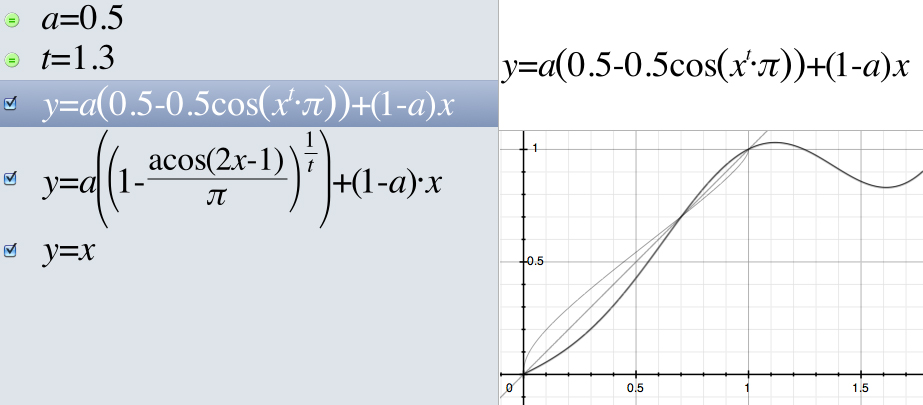
In short: I use an inverse function for the fact that it is mirrored to (y=x). So I can plug in a value x and get a y. This y can obviously plugged into the inverse function to get first x again.
Problem: I now want to be able to blend the groove into another, but the usual linear (hint hint) blending code does not behave like I expected it. To make it easier, I first tried to blend to y=x.
B(x)=alpha*F(x) + (1-alpha)*x;
iB(x)=alpha*iF(x) + (1-alpha)*x;
For alpha=1 we get the full curve. For alpha=0 we get the straight line. But for alpha between 0 and 1 B(x) and iB(x) are not mirrored anymore (close, but not enough), F(x) and iF(x) are still mirrored.
Is there a solution for that (besides quantizing the curve into line segments)? Any subject I should throw an eye on?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
您组合了两个函数 f(x) 和 g(x),因此 y = af(x) + (1-a) g(x)。给定一些 y、a、f 和 g,您想要找到 x。至少,我是这么理解的。
我不知道一般如何做到这一点(虽然我没有非常努力地尝试 - 我的意思是,值得询问其他人),但我怀疑对于“漂亮”形状的函数,就像你似乎正在使用的那样,牛顿法相当快。
您想要找到 x 使得 y = af(x) + (1-a) g(x)。换句话说,当 0 = af(x) + (1-a) g(x) - y 时。
所以让我们定义 r(x) = af(x) + (1-a) g(x) - y 并找到其中的“零”。从中间的猜测开始,x_0 = 0.5。计算 x_1 = x_0 - r(x_0) / r'(x_0)。重复。如果你幸运的话,这将快速收敛(如果没有,你可能会考虑定义相对于 y=x 的函数,你似乎已经在这样做,然后再试一次)。
请参阅维基百科
you are combining two functions, f(x) and g(x), so that y = a f(x) + (1-a) g(x). and given some y, a, f and g, you want to find x. at least, that is what i understand.
i don't see how to do this generally (although i haven't tried very hard - i mean, it would be worth asking someone else), but i suspect that for "nice" shaped functions, like you seem to be using, newton's method would be fairly quick.
you want to find x such that y = a f(x) + (1-a) g(x). in other words, when 0 = a f(x) + (1-a) g(x) - y.
so let's define r(x) = a f(x) + (1-a) g(x) - y and find the "zero" of that. start with a guess in the middle, x_0 = 0.5. calculate x_1 = x_0 - r(x_0) / r'(x_0). repeat. if you are lucky this will rapidly converge (if not, you might consider defining the functions relative to y=x, which you already seem to be doing, and trying it again).
see wikipedia
一般来说,这个问题无法用代数方法解决。
例如,考虑
y = 2e^x(逆x = log 0.5y)和
y = 2x(逆x = 0.5y )。将它们与权重 0.5 混合在一起得到 y = e^x+x ,众所周知,这里不可能仅使用初等函数求解 x ,尽管每件作品的逆面都很容易找到。
您将需要使用数值方法来近似逆,如上面安德鲁所讨论的。
This problem can't be solved algebraically, in general.
Consider for instance
y = 2e^x(inversex = log 0.5y)and
y = 2x(inversex = 0.5y).Blending these together with weight 0.5 gives
y = e^x+x, and it is well-known that it is not possible to solve forxhere using only elementary functions, even though the inverse of each piece was easy to find.You will want to use a numerical method to approximate the inverse, as discussed by andrew above.