中轴变换实现
How do I implement the Medial Axis Transform algorithm to transform the first image into the second?

(source: algorith at www.cs.sunysb.edu)
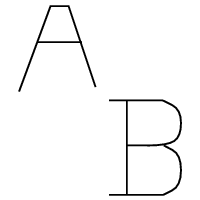
(source: algorith at www.cs.sunysb.edu)
What library in C++/C# have support for Medial Axis Transform?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(2)
互联网上有很多中轴变换的实现(我个人不使用 OpenCV 库,但是我确信它有一个不错的实现)。但是,您可以轻松地自己实现它。
为了进行中轴变换,我们只需要定义一个术语:简单点。
点 (P) 是简单点,当且仅当删除 P 不会影响前景或背景的连通分量的数量。因此,您必须决定背景和前景的连接(4或8) -为了工作,为两者选择不同的一个(如果您有兴趣为什么,请在谷歌上查找乔丹财产)。
中间变换轴可以通过顺序删除简单点来实现。如果没有更多的简单点,你就得到了最终的骨架。如果你只有端点或非简单点,你会得到弯曲的骨架(我不知道它的英文名称,这是罕见的 - 请纠正我)。您在问题中提供了后者的示例。
使用形态运算符可以轻松实现查找简单点一个查找表。提示:一个点是简单点,当且仅当在 3x3 本地窗口中,背景中的连通分量的数量为 1,并且前景中的连通分量的数量为 1。
There are many implementations of the medial axis transform on the Internet (personally I don't use OpenCV library but I'm sure it has a decent implementation). However, you could easily implement it yourself.
In order to perform medial axis transform, we need to define only one term: simple point.
A point (P) is simple point iff removing P doesn't effect the number of connected components of either the foreground or the background. So, you have to decide the connectivity (4 or 8) for the background and for the foreground - in order to work pick different one for both (if you are interested why, look up Jordan property on google).
Medial transform axis could be implemented by sequentally deleting simple points. You get the final skeleton if there are no more simple points. You get the curved skeleton (I don't know the english name for it which is rare - please correct me) if you only have endpoints OR non-simple points. You provided examples of the latter in your question.
Finding simple points could be easily implemented with morphological operators or a look-up table. Hint: a point is simple point iff the number of connected components in the background is 1 and the number of connected components in the foreground is 1 in a 3x3 local window.
此 C 库中有一个中轴变换可用:http://www.pinkhq.com/
还有很多其他相关功能。
查看此功能:http://www.pinkhq.com/medialaxis_8c.html
There is a medial axis transform available in this C Library:http://www.pinkhq.com/
There are lot other related functionalities.
Check out this Function:http://www.pinkhq.com/medialaxis_8c.html