python 中的命题演算

Question

我正在寻找一个在 python 中工作的命题微积分模块。

我的用户需要在文本区域中输入公式，然后我必须检查它是否正确。

我无法直接测试输入文本是否等于正确的文本，因为它没有考虑排列或此类因素。

这样的模块存在吗？

- 编辑-

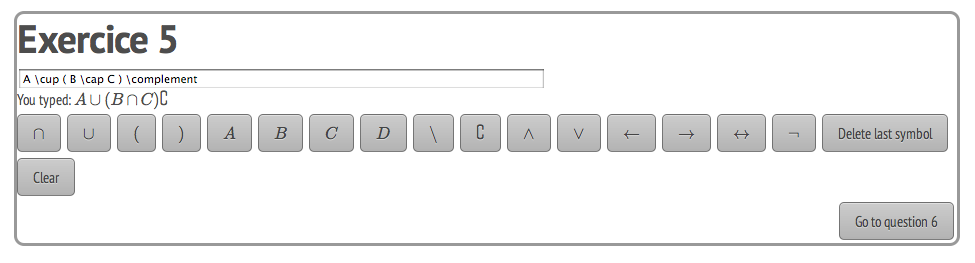
这是该项目的屏幕截图（设计未完成）：

Answer 1

这并不太难。您所需要做的就是（a）找到或（b）编写一个实用程序，该实用程序接受任意命题并生成真值表。然后，对于两个命题，您所需要做的就是生成两个真值表并检查所有行中的原子变量和最后一列是否匹配。

原子变量的数量是 O(2^n)，并且假设每个命题包含相同数量的原子变量。如果可能包含额外无用的原子变量（例如 OR（b 或 NOT b）相当于 a），则需要填充更简单命题的真值表以获得相同的行数。如果允许使用不同的原子变量，那么这会变得更加困难。

假设 P != NP，你不可能做得比 O(2^n) 更好，因为多项式解可以解决命题演算的一般可满足性问题。

要生成真值表，您需要 (a) 生成原子变量真值的所有 2^n 排列的列表（有很多方法可以做到这一点），以及 (b) 评估对真值的任意赋值的命题原子变量。然后制作两个表格并进行比较。瞧！

Answer 2

我刚刚偶然发现了这个问题。不知道是否还需要答案，但我建议使用 SymPy：

http:// /docs.sympy.org/dev/modules/logic.html

Answer 3

A，B，C ...在您提供的示例中似乎是集合，
不是提议。这是有可能的
也关于这些类型的陈述，但不是
据我所知，命题逻辑。

从语义上比较这些陈述，这就是
你想要在这里，需要更复杂的逻辑，
但更简单的方法也许是重写
所有陈述都采用可通过纯文本进行比较的形式
比较。即通过忽略交换律，这
语句

 (A ⋃ B) ⋂ C

也将与此语句相同

 C ⋂ (B ⋃ A)

即使这不是一个完美的设置， ，因为可能
是不被认可的等效陈述，
使用逻辑等价来解决这个问题的过程将
会困难得多。使用重写逻辑或多或少
只需很少的努力就能得到你想要的东西。基本上都是你
需要指定哪些二元运算符是
可交换的。重写等价的几个方程
还添加了语句，您可能需要添加更多...
我用 Maude http://maude.cs.uiuc.edu/ 写了一些东西

    mod VennDiagram is

    --- sorts
    sort Set .
    sort Statement .
    subsort Set < Statement .

    --- propositional formulas
    op a : -> Set .
    op b : -> Set .
    op c : -> Set .
    op d : -> Set .
    op e : -> Set .
    op f : -> Set .
    op g : -> Set .
    op h : -> Set .
    op i : -> Set .
    op j : -> Set .
    --- and so on ....

    --- connectives
    op ¬_  : Statement -> Statement .
    op _∁  : Statement -> Statement . --- complement
    op _∨_ : Statement Statement -> Statement [ comm ] .
    op _∧_ : Statement Statement -> Statement [ comm ] .
    op _↔_ : Statement Statement -> Statement [ comm ] .
    op _→_ : Statement Statement -> Statement .
    op _⋂_ : Statement Statement -> Statement [ comm ] .
    op _⋃_ : Statement Statement -> Statement [ comm ] .
    op _←_ : Statement Statement -> Statement .


    vars S1 S2 S3 S4 : Statement . --- variables

    --- simplify statemens through equivalence

    eq S1 → S2 = ¬ S1 ∨ S2 .
    eq S1 ↔ S2 = (S1 → S2) ∧ (S2 → S1) .
    eq ¬ ¬ S1 = S1 .
    eq S1 ← S2 = S2 → S1 .
    eq ¬ ( S1 ∧ S2 ) = (¬ S1) ∨ (¬ S2) .
    --- possibly other equivalences as well..

    endm

    --- check equality

    reduce a ↔ b == (b → a) ∧ (a → b) .
    reduce ¬ a ↔ ( a ∨ b ) ==  ¬ a ↔ ( b ∨ a ) .
    reduce (a ⋃ b) ⋂ c == c ⋂ (b ⋃ a) .

    --- what you need to do is to compare the right answer
    --- with a student answer through a simple comparison..
    --- reduce StudentAnswer == RightAnswer