从二值图像中分割圆形形状
我有几个二值图像,我的任务是分割圆形形状。这些圆不是完美的圆,但它们看起来都像圆。以下是一些示例图像和我需要的图像:
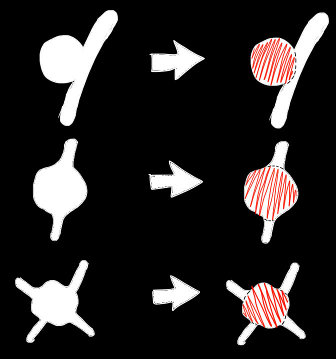
正如您从上面看到的,左侧图像是原始图像图像,而正确的图像就是我需要做的。圆圈与其他形状相交,但我只想要圆圈,如红色所示。需要用假想线来闭合圆。在这种情况下,我可以在图像处理中做什么?
编辑:以防万一,上面的图像已损坏,此处: http://imageshack .us/photo/my-images/835/circleonly.jpg/
I have several binary images and my task is to segment circle-like shape. The circles are not perfect rounded circle, but all of them will look like circle. Here are some example images and what I need:

As you can see from above, the left images are original images, and the right images are what I need to do. The circles intersect with other shapes, but I only want the circle, as indicated in red. The imaginary lines to close the circle will be required. What can I do in this case in Image Processing?
EDIT: in case, the image above is broken, here: http://imageshack.us/photo/my-images/835/circleonly.jpg/
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
您知道您正在寻找的磁盘的半径吗?
如果是的话,形态开口(侵蚀然后扩张)将是简单的,而且非常快。使用 Mathematica 的结果:
如果没有,按照其他建议,计算轮廓图像,然后使用霍夫变换将是一个值得追求的方法。上图显示了轮廓图像。
Do you know the radii of the disks you are looking for?
If yes, morphological openings (erosion then dilation) would be straightforward, and very fast. The result using Mathematica:
If not, as other proposed, computing the contour image and then using the Hough transform would be a method worth pursuing. The image just above shows the contour image.
您可以使用霍夫变换,首先您需要的是边缘图像,然后使用霍夫变换,就像您在本文中看到的
http://www.cis.rit.edu/class/simg782/lectures/lecture_10/lec782_05_10。 pdf
http://www.sci.utah.edu/~gerig/CS6640- F2010/FINALPROJECT/Ballard-GHT-1981.pdf
http://www.sciencedirect.com/science/article/pii/003132039290064P
http://www.markschulze.net/java/hough/
You can use hough transform, first you need is the edge image then you use a hough transform like you can see in this papers
http://www.cis.rit.edu/class/simg782/lectures/lecture_10/lec782_05_10.pdf
http://www.sci.utah.edu/~gerig/CS6640-F2010/FINALPROJECT/Ballard-GHT-1981.pdf
http://www.sciencedirect.com/science/article/pii/003132039290064P
http://www.markschulze.net/java/hough/