为什么这个正交顶点着色器不能产生正确的答案?
我的问题是,我有一个(工作的)正交顶点和片段着色器对,允许我通过传入的“translateX”和“translateY”制服指定精灵的中心X和Y。我乘以硬编码的projectionMatrix,效果很好。就正交操作而言,一切正常。我传入该着色器的几何体以 0, 0, 0 为中心点。
我现在想弄清楚平移后中心点(局部坐标空间中的 0, 0, 0)变成了什么。我需要在片段着色器中知道这些信息。我假设我可以在 0, 0, 0 处创建一个向量,然后应用相同的平移。但是,我没有得到正确的答案。
我的问题:我做错了什么,我该如何调试正在发生的事情?我知道计算的值一定是错误的,但我不知道它是什么。 (我的平台是 OS X 上的 Xcode 4.2,为 OpenGL ES 2.0 iOS 开发)
这是我的顶点着色器:
// Vertex Shader for pixel-accurate rendering
attribute vec4 a_position;
attribute vec2 a_texCoord;
varying vec2 v_texCoord;
uniform float translateX;
uniform float translateY;
// Set up orthographic projection
// this is for 640 x 960
mat4 projectionMatrix = mat4( 2.0/960.0, 0.0, 0.0, -1.0,
0.0, 2.0/640.0, 0.0, -1.0,
0.0, 0.0, -1.0, 0.0,
0.0, 0.0, 0.0, 1.0);
void main()
{
// Set position
gl_Position = a_position;
// Translate by the uniforms for offsetting
gl_Position.x += translateX;
gl_Position.y += translateY;
// Translate
gl_Position *= projectionMatrix;
// Do all the same translations to a vector with origin at 0,0,0
vec4 toPass = vec4(0, 0, 0, 1); // initialize. doesn't matter if w is 1 or 0
toPass.x += translateX;
toPass.y += translateY;
toPass *= projectionMatrix;
// this SHOULD pass the computed value to my fragment shader.
// unfortunately, whatever value is sent, isn't right.
//v_translatedOrigin = toPass;
// instead, I use this as a workaround, since I do know the correct values for my
// situation. of course this is hardcoded and is terrible.
v_translatedOrigin = vec4(500.0, 200.0, 0.0, 0.0);
}
编辑: 为了响应我的正交矩阵错误,以下是 wikipedia 必须介绍正交投影,并且我的-1看起来不错。因为在我的例子中,我的垫子的第四个元素应该是 -((right+left)/(right-left)) ,它是 960 左边的 0 的右边,所以 -1 * (960/960) 是 -1 。
编辑:我可能在这里发现了根本问题 - 你觉得怎么样?
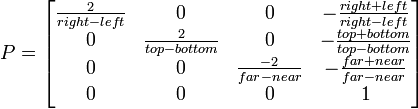
My issue is that I have a (working) orthographic vertex and fragment shader pair that allow me to specify center X and Y of a sprite via 'translateX' and 'translateY' uniforms being passed in. I multiply by a projectionMatrix that is hardcoded and works great. Everything works as far as orthographic operation. My incoming geometry to this shader is based around 0, 0, 0 as its center point.
I want to now figure out what that center point (0, 0, 0 in local coordinate space) becomes after the translations. I need to know this information in the fragment shader. I assumed that I can create a vector at 0, 0, 0 and then apply the same translations. However, I'm NOT getting the correct answer.
My question: what I am I doing wrong, and how can I even debug what's going on? I know that the value being computed must be wrong, but I have no insight in to what it is. (My platform is Xcode 4.2 on OS X developing for OpenGL ES 2.0 iOS)
Here's my vertex shader:
// Vertex Shader for pixel-accurate rendering
attribute vec4 a_position;
attribute vec2 a_texCoord;
varying vec2 v_texCoord;
uniform float translateX;
uniform float translateY;
// Set up orthographic projection
// this is for 640 x 960
mat4 projectionMatrix = mat4( 2.0/960.0, 0.0, 0.0, -1.0,
0.0, 2.0/640.0, 0.0, -1.0,
0.0, 0.0, -1.0, 0.0,
0.0, 0.0, 0.0, 1.0);
void main()
{
// Set position
gl_Position = a_position;
// Translate by the uniforms for offsetting
gl_Position.x += translateX;
gl_Position.y += translateY;
// Translate
gl_Position *= projectionMatrix;
// Do all the same translations to a vector with origin at 0,0,0
vec4 toPass = vec4(0, 0, 0, 1); // initialize. doesn't matter if w is 1 or 0
toPass.x += translateX;
toPass.y += translateY;
toPass *= projectionMatrix;
// this SHOULD pass the computed value to my fragment shader.
// unfortunately, whatever value is sent, isn't right.
//v_translatedOrigin = toPass;
// instead, I use this as a workaround, since I do know the correct values for my
// situation. of course this is hardcoded and is terrible.
v_translatedOrigin = vec4(500.0, 200.0, 0.0, 0.0);
}
EDIT: In response to my orthographic matrix being wrong, the following is what wikipedia has to say about ortho projections, and my -1's look right. because in my case for example the 4th element of my mat should be -((right+left)/(right-left)) which is right of 960 left of 0, so -1 * (960/960) which is -1.
EDIT: I've possibly uncovered the root issue here - what do you think?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
为什么你的正交矩阵每列底部都有-1?这些应该是零。当然,这不会影响任何事情。
我更关心的是:
这意味着什么?矩阵乘法不是可交换的;
M * a与a * M不同。那么您希望gl_Position在哪一边相乘呢?奇怪的是,GLSL 规范没有说明(我对此提交了错误报告)。因此,您应该选择保证有效的方法:
此外,您应该使用正确的矢量化代码。您应该拥有一套
translate制服,即vec2。然后你就可以执行gl_Position.xy = a_position.xy + translate;。您必须用常量填充 Z 和 W (gl_Position.zw = vec2(0, 1);)。GLSL 中的矩阵是列主。前四个值是矩阵的第一列,而不是第一行。您正在与转置的正交矩阵相乘。
Why does your ortho matrix have -1's in the bottom of each column? Those should be zeros. Granted, that should not affect anything.
I'm more concerned about this:
What does that mean? Matrix multiplication is not commutative;
M * ais not the same asa * M. So which side do you expectgl_Positionto be multiplied on?Oddly, the GLSL spec does not say (I filed a bug report on this). So you should go with what is guaranteed to work:
Also, you should use proper vectorized code. You should have one
translateuniform, which is avec2. Then you can just dogl_Position.xy = a_position.xy + translate;. You'll have to fill in the Z and W with constants (gl_Position.zw = vec2(0, 1);).Matrices in GLSL are column major. The first four values are the first column of the matrix, not the first row. You are multiplying with a transposed ortho matrix.
我必须同意尼可波拉斯的观点。为了让事情顺利进行而发生的两个错误令人沮丧,但这并不能减少他们的错误。事实上,事情出现在你期望的地方可能是因为你的矩阵的平移部分是 0, 0, 0。
你发布的方程是正确的,但符号是行主要,而 OpenGL 是列主要:
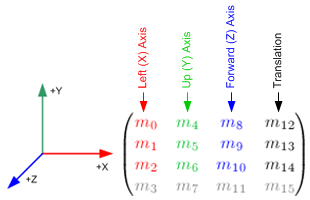
我在启动每个新项目时都会遇到这些问题。 这个网站是一个非常好的资源,帮助我把这些事情搞清楚。他们还有另一个关于投影矩阵的页面。
如果您不确定正交投影是否正确(现在不正确),请尝试将相同的值插入 glOrtho 和 从 GL_PROJECTION 读取值。
I have to echo Nicol Bolas's sentiment. Two wrongs happening to make things work is frustrating, but doesn't make them any less wrong. The fact that things are showing up where you expect is likely because the translation portion of your matrix is 0, 0, 0.
The equation you posted is correct, but the notation is row major, and OpenGL is column major:

I run afoul of this stuff every new project I start. This site is a really good resource that helped me keep these things straight. They've got another page on projection matrices.
If you're not sure if your orthographic projection is correct (right now it isn't), try plugging the same values into glOrtho, and reading the values back out of GL_PROJECTION.