具有一定惯性的路径算法

Question

我正在尝试开发一款游戏。

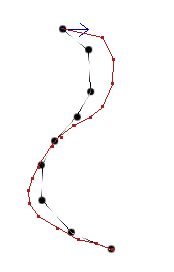
我有一个起点和起始向量（蓝色），接下来我在屏幕上绘制路径（黑色）我想以一定的惯性或有限的角度和步数跟随每一个转弯，这应该会导致一条红线。

您对如何编写此类算法有什么建议吗？

Answer 1

您只需创建一个微分方案，即离散时刻的模型速度和源点坐标。例如，假设您修复了一些 dt = 0.1 sec，起始速度由蓝色矢量指定为 v0。我们从x0开始。
假设 y[j] 是黑色路径的点。

令 x1 = x0 + v1 * dt，其中 v1 = v0 + (y[k(x0)+1] - x0) * f(abs(y[k(x0)+1) ] - x_0))。哪里
k(x0)是y[j]中最接近x0点的索引，
f(x) 是一个函数，描述将您的轨迹拉至定义路径的“力”。它仅为非负xes 定义。

此模型将您的轨迹拉至定义路径中最接近轨迹上当前建模位置的下一个点。

f(x) 的一个很好的例子是对引力进行建模：f(x) = K/(x * x)，其中 K code> 应该通过实验进行调整，以给出自然的期望结果。

然后 x2 = x1 + v2 * dt，其中 v2 = v1 + (y[k(x1) + 1] - x1) * f(abs(y[k(x1) + 1) ] - x_1)) 等等：

x[n+1] = x[n] + v[n+1] * dt，其中 v[n+1 ] = v[n] + (y[k(x[n]) + 1] - x[n]) * f(abs(y[k(x[n])+1] - x[n]))...

您必须在此处调整dt 和K。 dt 应足够小以使轨迹平滑。较大的K使轨迹更加接近精确定义，较小的K使其更加宽松。

编辑现在实际上当我想了一下，我明白力函数f的选择不好，因为重力允许空间速度，即你的轨迹的能力如果初始速度太大，就会无限地飞离目标。因此，您应该构造另一个函数，可能只是类似于 f(x) = K x 或 f(x) = K x ^ alpha 的函数，其中 阿尔法> 0 。你看，这个方案非常通用，所以你应该尝试一下。

Answer 2

另一种选择是做这样的事情......

  1. Compute the average value of k points in the target path
     to get (<x>,<y>).
  2, Compte the angle between the most recent point in the path
     and (<x>,<y>) and turn that way; if the angle is too big,
     turn as hard as possible.
  3. Recompute (<x>,<y>) for the next set of k elements by sliding
     the window by 1; repeat step 2.

这可能会产生相当合适的行为。我会讲一个例子，但这会相当乏味。请注意，这与 unkulunkulu 概述的方法类似，但在方法方面略有不同。