Matplotlib 轮廓不起作用
我正在尝试绘制蝙蝠侠方程。 sympy 或 matplotlib 中的解决方案会很棒(圣人并不酷,因为我使用的是 Windows)。问题是,如果我注释掉某些部分,则图形的部分会出现,但对于所有 F *= 部分,我会得到一个空白图。
import matplotlib.pyplot
from numpy import arange
from numpy import meshgrid
from numpy import sqrt
from numpy import real
delta = 0.01
xrange = arange(-7.0, 7.0, delta)
yrange = arange(-3.0, 3.0, delta)
x, y = meshgrid(xrange,yrange)
F = 1
F *= (((x/7) ** 2) * sqrt(abs(abs(x) - 3)/(abs(x) - 3)) + ((y / 3) ** 2) * sqrt(abs(y + (3 * sqrt(33)) / 7)/(y + (3 * sqrt(33)) / 7)) - 1)
F *= (abs(x/2) - ((3 * sqrt(33) - 7)/112) * x**2 - 3 + sqrt(1 - (abs(abs(x) - 2) - 1) ** 2 ) - y)
F *= (9 * sqrt(abs((abs(x) - 1) * (abs(x) - 3/4))/((1 - abs(x)) * (abs(x) - 3/4))) - 8 * abs(x) - y)
F *= (3 * abs(x) + 0.75 * sqrt(abs((abs(x) - 3/4) * (abs(x) - 1/2))/((3/4 - abs(x)) * (abs(x) - 1/2))) - y)
F *= ((9/4) * sqrt(abs((x - 1/2) * (x + 1/2))/((1/2 - x) * (1/2 + x))) - y)
F *= ((6 * sqrt(10)) / 7 + (3/2 - abs(x)/2) * sqrt(abs(abs(x) - 1)/(abs(x) - 1)) - ((6 * sqrt(10))/ 14) * sqrt(4 - (abs(x) - 1) ** 2 ) - y)
G = 0
matplotlib.pyplot.contour(x, y, (F - G), [0])
matplotlib.pyplot.show()
这是怎么回事?如果图形对于一个被乘数为零,那么无论我在其中放入哪些其他被乘数,它仍然应该为零。
蝙蝠侠方程的来源:http://www.reddit.com/r/图片/评论/j2qjc/do_you_like_batman_do_you_like_math_my_math/
I'm trying to plot the batman equation. A solution in sympy or matplotlib will be great (sage isn't cool because I'm using windows). The problem is that if I comment out certain parts the part of the figure appears but with all the F *= parts, I get a blank plot.
import matplotlib.pyplot
from numpy import arange
from numpy import meshgrid
from numpy import sqrt
from numpy import real
delta = 0.01
xrange = arange(-7.0, 7.0, delta)
yrange = arange(-3.0, 3.0, delta)
x, y = meshgrid(xrange,yrange)
F = 1
F *= (((x/7) ** 2) * sqrt(abs(abs(x) - 3)/(abs(x) - 3)) + ((y / 3) ** 2) * sqrt(abs(y + (3 * sqrt(33)) / 7)/(y + (3 * sqrt(33)) / 7)) - 1)
F *= (abs(x/2) - ((3 * sqrt(33) - 7)/112) * x**2 - 3 + sqrt(1 - (abs(abs(x) - 2) - 1) ** 2 ) - y)
F *= (9 * sqrt(abs((abs(x) - 1) * (abs(x) - 3/4))/((1 - abs(x)) * (abs(x) - 3/4))) - 8 * abs(x) - y)
F *= (3 * abs(x) + 0.75 * sqrt(abs((abs(x) - 3/4) * (abs(x) - 1/2))/((3/4 - abs(x)) * (abs(x) - 1/2))) - y)
F *= ((9/4) * sqrt(abs((x - 1/2) * (x + 1/2))/((1/2 - x) * (1/2 + x))) - y)
F *= ((6 * sqrt(10)) / 7 + (3/2 - abs(x)/2) * sqrt(abs(abs(x) - 1)/(abs(x) - 1)) - ((6 * sqrt(10))/ 14) * sqrt(4 - (abs(x) - 1) ** 2 ) - y)
G = 0
matplotlib.pyplot.contour(x, y, (F - G), [0])
matplotlib.pyplot.show()
What's going on here? If the graph is zero for one multiplicand, it should still be so no matter which other multiplicands I throw in there.
source of the batman equation: http://www.reddit.com/r/pics/comments/j2qjc/do_you_like_batman_do_you_like_math_my_math/
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(3)
sqrt 的参数对于很多点都是负数,所以最终的结果都是 NaN。您可以将每个因素绘制如下:
结果图:
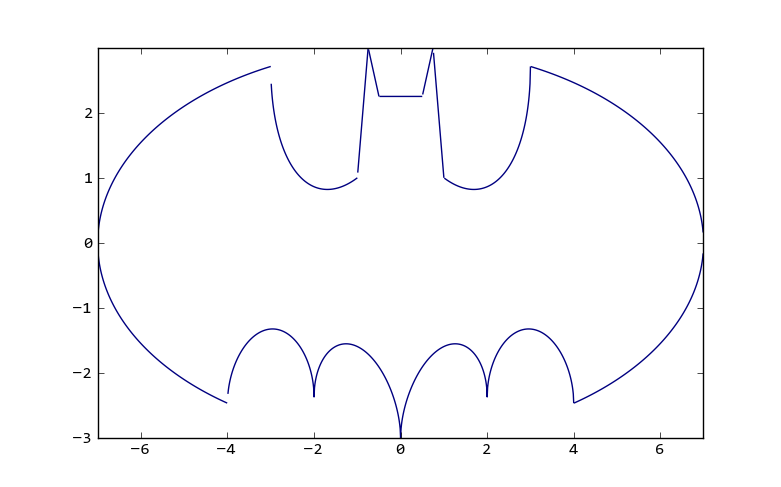
The parameter of sqrt is negative for many points, so the finally products are all NaN. You can plot every factor as following:
the result plot:

我知道这可能看起来很蹩脚,但是如何创建一个 x 值列表,然后计算每个位置的“蝙蝠侠”的值,并将其存储在另一个列表中。您可以定义一个函数“batman”,它计算您传入的每个 x 值的 y 值。
然后只需使用 matplotlib 绘制这些列表即可。
编辑:由于您已经创建了 numpy 数组来存储结果,因此您可以在计算 y 值时使用它们。
I know this might seem lame, but how about creating a list of x values, and then computing the value of "batman" at each of those positions, and storing in another list. You could define a function "batman" which computes the y value for each x value you pass in.
Then just plot those lists with matplotlib.
EDIT: Since you've made numpy arrays already to store the results, you could use those when computing the y values.
我什至不确定这个方程是如何工作的,因为我看到第一项(在第一个平方根下,当abs(x)= 3时)除以零,并且虚数出现在最后一项(在最后的平方根,当 {abs(x)-1}^2 > 4,即 x > 3 或 x < -3)。
我在这里缺少什么?是否仅使用结果的实部,并且忽略或近似除以零?
运行这个,我确实看到了很多 RunTimeWarnings,并且 matplotlib 不太可能完全混淆要使用哪些数字(NaN、Infs;最后尝试打印 F)。当 NaN 或 Inf 数量相对较少时,看起来它仍然可以正常工作,这可以解释您看到的是该图的一部分。
我认为 matplotlib 的轮廓很好,只是被输入混淆了。
I'm not even sure how this equation would work, since I see divisions by zero arising in the first term (under the first square root, when abs(x) = 3), and imaginary numbers showing up in the last term (under the last square root, when {abs(x)-1}^2 > 4, ie x > 3 or x < -3).
What am I missing here? Is only the real part of the result used, and are divisions by zero ignored or approximated?
Running this, I do indeed see lots of RunTimeWarnings, and it is not unlikely matplotlib would get totally confused what numbers to work with (NaNs, Infs; trying print F at the end). Looks like it still manages when there's only a relatively low number of NaNs or Infs, which would explain that you're seeing part of the figure.
I'd think matplotlib's contour is fine, just confused by the input.