谱聚类、图像分割和特征向量

Question

根据《Computer Vision a Modern Approach》第 425 页一书，我尝试使用特征向量进行图像分割。

http://dl.dropbox.com/u/ 1570604/tmp/comp-vis-modern-segment.pdf

作者提到可以在矩阵A中捕获图像像素仿射，然后我们可以最大化w^TA w乘积其中 w 是权重。经过一些代数之后，我们可以得到 Aw = lambda w，找到 w 就像找到特征向量一样。那么寻找最佳簇就是寻找特征向量最大的特征值，该特征向量内的值就是簇隶属度值。我写了这段代码

import matplotlib.pyplot as plt
import numpy as np

Img = plt.imread("twoObj.jpg")
(n,dummy) = Img.shape
Img2 = Img.flatten()
(nn,) = Img2.shape

A = np.zeros((nn,nn))

for i in range(nn):
    for j in range(nn):
        N=Img2[i]-Img2[j];
        A[i,j]=np.exp(-(N**2))

V,D = np.linalg.eig(A)
V = np.real(V)
a = np.real(D[1])

threshold = 1e-10 # filter
a = np.reshape(a, (n,n))
Img[a<threshold] = 255
plt.imshow(Img)
plt.show()

图像

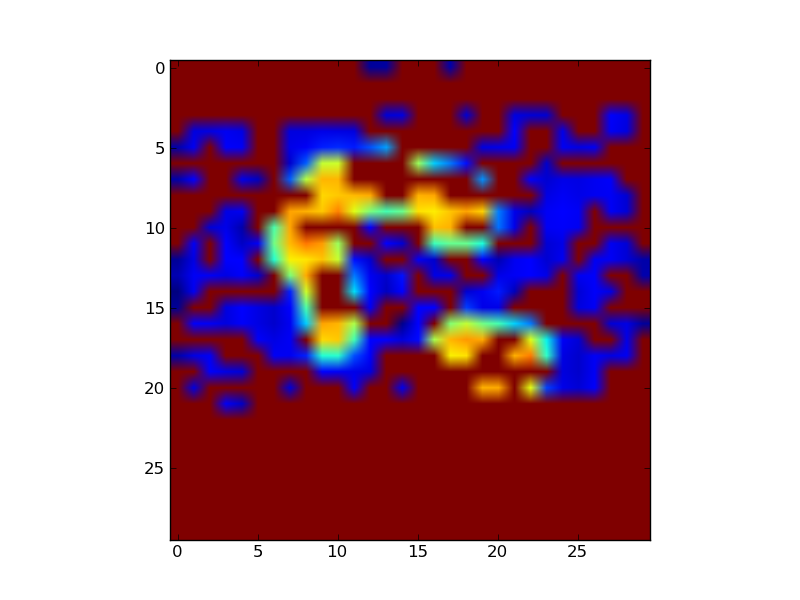
我可以从中得到的最佳结果如下。我有一种感觉，结果会更好。

特征值在 Numpy 中从最大到最小排序，我尝试了第一个，但不起作用，然后我尝试了第二个，结果如下所示。阈值是通过反复试验来选择的。关于如何改进该算法有什么想法吗？

Answer 1

我刚刚在 Mathematica 中尝试了该算法，它在您的图像上运行良好，因此您的代码中一定存在细微的错误。

这部分：

V,D = np.linalg.eig(A)
V = np.real(V)
res = n_max(V,1) # take largest 
idx = res[0][1][0] 
a = np.real(D[idx]) # look at corresp eigv

看起来很奇怪：我知道的所有线性代数包都会返回已排序的特征值/特征向量，因此您只需获取列表中的第一个特征向量即可。这就是对应于最高特征值的那个。尝试绘制特征值列表来确认这一点。

另外，你从哪里得到固定阈值？您是否尝试过标准化图像以显示它？

无论如何，我得到的前 3 个特征向量的结果是：

这是我使用的 Mathematica 代码：

pixels = Flatten[image];
weights = Table[N[Exp[-(pixels[[i]] - pixels[[j]])^2]], {i, 1, 900}, {j, 1, 900}];
eigenVectors = Eigenvectors[weights];
ImageAdjust[Image[Partition[eigenVectors[[1]], 30]]]