求两个直方图的卷积

Question

两个随机变量 x 和 y 之和的概率分布由各个分布的卷积给出。我在进行数值计算时遇到了一些麻烦。在下面的示例中，x 和 y 是均匀分布的，它们各自的分布近似为直方图。我的推理是，应该对直方图进行卷积以给出 x+y 的分布。

from numpy.random import uniform
from numpy import ceil,convolve,histogram,sqrt
from pylab import hist,plot,show

n = 10**2

x,y = uniform(-0.5,0.5,n),uniform(-0.5,0.5,n)

bins = ceil(sqrt(n))

pdf_x = histogram(x,bins=bins,normed=True)
pdf_y = histogram(y,bins=bins,normed=True)

s = convolve(pdf_x[0],pdf_y[0])

plot(s)
show()

给出以下内容，

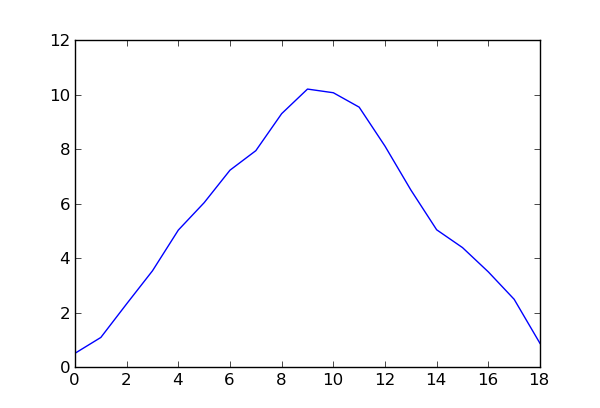
换句话说，如预期的那样，是三角形分布。但是，我不知道如何找到 x 值。如果有人能在这里纠正我，我将不胜感激。

Answer 1

为了继续前进（朝着更模糊的细节），我进一步调整了您的代码，如下所示：

from numpy.random import uniform
from numpy import convolve, cumsum, histogram, linspace

s, e, n= -0.5, 0.5, 1e3
x, y, bins= uniform(s, e, n), uniform(s, e, n), linspace(s, e, n** .75)
pdf_x= histogram(x, normed= True, bins= bins)[0]
pdf_y= histogram(y, normed= True, bins= bins)[0]
c= convolve(pdf_x, pdf_y); c= c/ c.sum()
bins= linspace(2* s, 2* e, len(c))
# a simulation
xpy= uniform(s, e, 10* n)+ uniform(s, e, 10* n)
c2= histogram(xpy, normed= True, bins= bins)[0]; c2= c2/ c2.sum()

from pylab import grid, plot, show, subplot
subplot(211), plot(bins, c)
plot(linspace(xpy.min(), xpy.max(), len(c2)), c2, 'r'), grid(True)
subplot(212), plot(bins, cumsum(c)), grid(True), show()

因此，给出如下图：

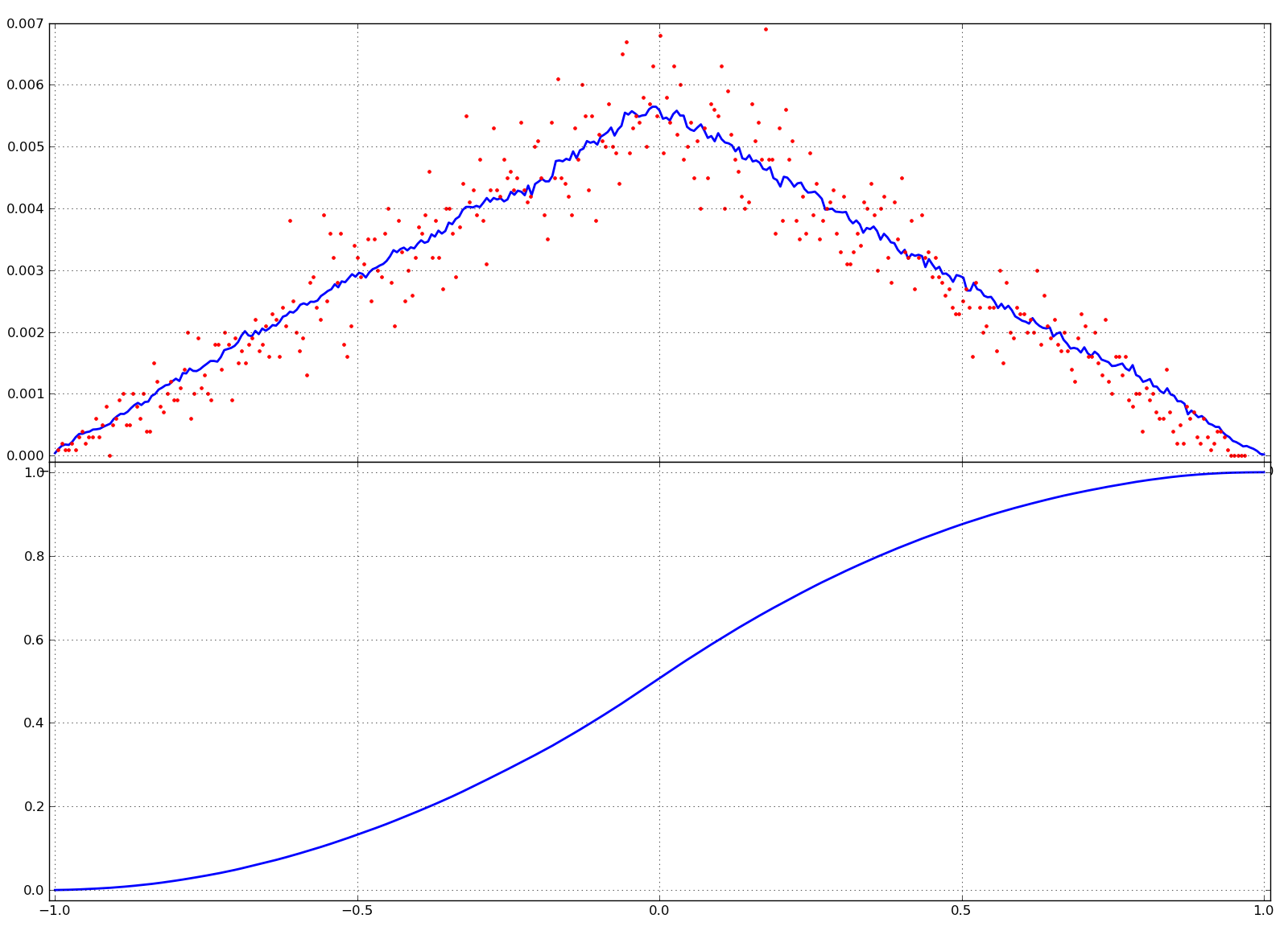
其中上部代表 PDF（蓝线），它确实看起来很三角形，而模拟（红点）则反映了三角形形状。下半部分代表 CDF，它看起来也很好地遵循预期的 S 曲线。