如何计算 STL 文件中存储的对象的体积?
我有 .stl(STL 是 3D Systems 创建的立体光刻 CAD 软件的原生文件格式) 文件,我必须从中计算体积。我该怎么做?我使用下面的计算,但体积不等于其他软件计算的体积
float x1,y1,z1;
float x2,y2,z2;
float x3,y3,z3;
。上面是顶点。三角形只是一个数据结构,保存带有每个三角形顶点的对象。
totalVolume += currentVolume =
(triangles[i].x1*triangles[i].y2*triangles[i].z3 -
triangles[i].x1*triangles[i].y3*triangles[i].z2 -
triangles[i].x2*triangles[i].y1*triangles[i].z3 +
triangles[i].x2*triangles[i].y3*triangles[i].z1 +
triangles[i].x3*triangles[i].y1*triangles[i].z2 -
triangles[i].x3*triangles[i].y2*triangles[i].z1) / 6;
是否也涉及到法向量的计算?
I have .stl (STL is a file format native to the stereolithography CAD software created by 3D Systems) files, from which I must calculate the volume. How do I do this? I'm using the calculation below but the volume is not equal to that calculated by other software
float x1,y1,z1;
float x2,y2,z2;
float x3,y3,z3;
The above are the vertices. triangles is just a data structure holding an object with the vertices of each triangle.
totalVolume += currentVolume =
(triangles[i].x1*triangles[i].y2*triangles[i].z3 -
triangles[i].x1*triangles[i].y3*triangles[i].z2 -
triangles[i].x2*triangles[i].y1*triangles[i].z3 +
triangles[i].x2*triangles[i].y3*triangles[i].z1 +
triangles[i].x3*triangles[i].y1*triangles[i].z2 -
triangles[i].x3*triangles[i].y2*triangles[i].z1) / 6;
Do you also involve the calculation with the normal vector?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
维基百科的多面体文章讨论了多面体的体积。任何有效的 STL 镶嵌必须精确地是一个多面体,其中每个面都是一条边,因此此处讨论的公式成立。
假设顶点逆时针方向(向下看向外的法线),以下展开式成立:
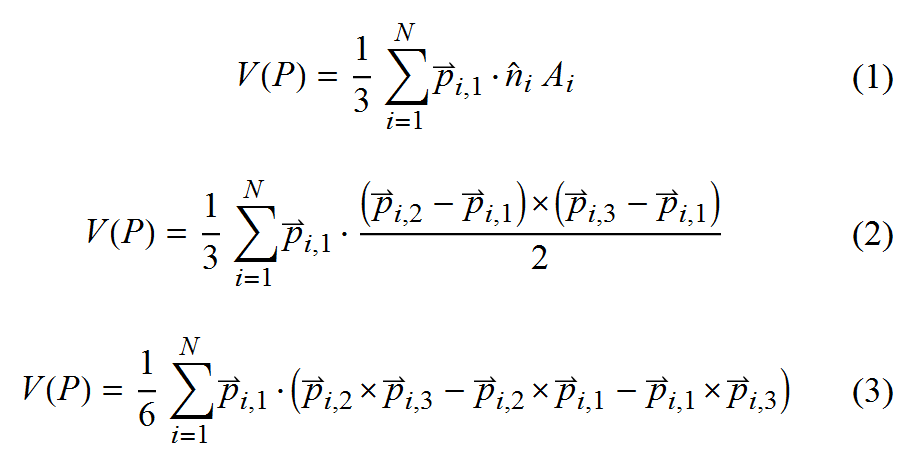
方程 1 只是多面体的散度公式。 p[i,j] 是第 i 个三角形的第 j 个顶点(作为来自原点的向量)。
方程 2 利用以下事实对此进行了扩展:两个三角形边(平行四边形)的叉积是三角形的法向量,其大小是三角形面积的两倍。
顺便说一句,这就是为什么三角形法线没有出现在你的表达式中,即使你的直觉告诉你它应该以某种方式存在。已经在汤里了!
方程 3 只是使用叉积的分配性质来展开方程 2,并且向量叉本身就是零向量。
从方程 3 得到的体积根据三角形的方向进行标记。我已经调整了我的公式以与您的代码一致,但您可能会得到负面结果。如果是的话,就取绝对值。
现在用你的符号写出被加数(除了我不费心放入重复的三角形[i])我得到:
这与你所写的完全匹配(除了顺序)!
因此,有几种可能性:
(1) 也许您的 STL 文件有缺陷,并且三角形的方向不一致。您可以通过验证三角形是否使用每条边一次在正向方向和一次在相反方向来检查这一点。我所说的“边”是指属于同一个三角形的一对顶点 (p[r], p[s])。我正在更改表示法并使用下标来指示文件中唯一索引的顶点,而不是像上面使用两个索引表示法那样表示顶点相对于面的索引)。
如果一个三角形在其定向边列表中具有边(p[r],p[s]),则其他一些三角形必须具有(p[s],p[r])(相同的顶点,相反的顺序)在它的定向边列表中。
(2) 曲面细分不封闭。这与 1 的测试相同,只是如果只有一个三角形使用边,则无论方向如何,它都是开放的。
(3)我敢提吗?您确定已初始化currentVolume吗?
(4) 你得到了正确的答案,但体积却是负数,你误以为方法是错误的。请参阅我上面的评论。
The volume of polyhedra is discussed in the polyhedron article in Wikipedia. Any valid STL tessellation must be precisely a polyhedron where each facet is a side, so the formula discussed there holds.
Assuming the vertices are oriented counter-clockwise (looking down the outward normals) the following expansion holds:
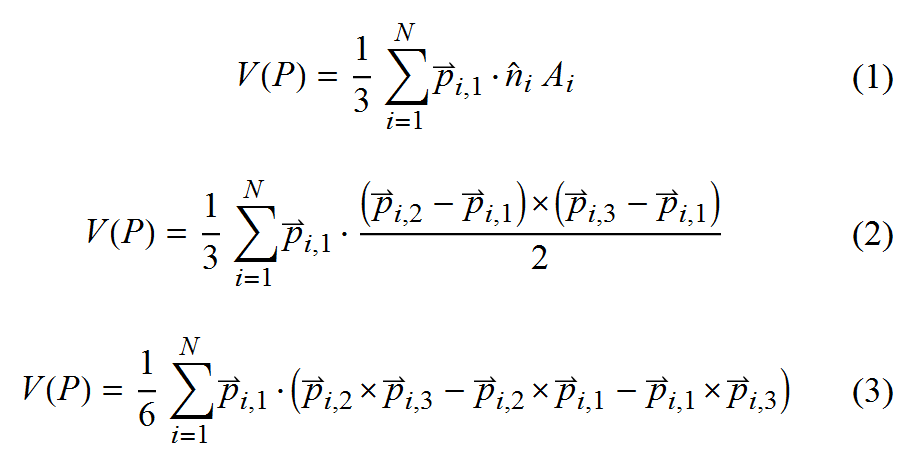
Equation 1 is just the divergence formula for polyhedra. The p[i,j] are the jth vertex (as a vector from the origin) of the ith triangle.
Equation 2 expands this by using the fact that the the cross product of the two triangle sides (a parallelogram) is a normal vector of the triangle with magnitude twice the area of the triangle.
By the way, this is why the triangle normal doesn't show up in your expression even though your intuition says it should be there somehow. It's already in the soup!
Equation 3 just expands equation 2 using the distributive properties of the cross product, and that fact that a vector cross itself is the zero vector.
The volume you get from equation 3 is signed according to the orientation of the triangles. I've aligned my formulation to agree with your code, but you may have a negative result. If so, just take the absolute value.
Now writing out the summand in your notation (except that I don't bother putting in the repeated triangle[i]) I get:
This exactly matches what you've written (except for order)!
So there are a couple of possibilities:
(1) Perhaps your STL file is flawed and the triangles aren't all oriented consistently. You can check this by verifying that each edge is used by a triangle once in the forward direction, and once in the opposite direction. By and "edge" I mean a pair of vertices (p[r], p[s]) that are part of the same triangle. I'm changing notation and using the subscript to indicate the uniquely indexed vertex in the file, not the index of the vertex relative to the face as I did with the two-index notation above).
If a triangle has edge (p[r], p[s]) in its list of oriented edges, then some other triangle must have (p[s], p[r]) (same vertices, reversed order) in it's list of oriented edges.
(2) The tessellation isn't closed. This is the same test as 1, except that it's open if only one triangle uses the edge, regardless of orientation.
(3) Dare I mention it? Are you sure you initialized currentVolume?
(4) You get the right answer, but the volume is negative and you're fooled into thinking the method is wrong. See my comments above.
int 与 double 问题?
/ 6;也许应该是/6.0;
int versus double problem?
/ 6; maybe should be / 6.0;