相对于矩形裁剪多边形
今天我有一个(简单的)渲染问题要问你。我当前的项目从文件中获取数据以生成 SVG 文件。由于 SVG 格式,将事物绘制为多边形非常容易,但我有一个问题:我的一些多边形在页面内外(这意味着它们的某些部分显示,而其余部分则不显示,因为事实)它们超出了显示限制)。为了优化最终的 SVG 文件,我需要将多边形简化为更简单的形式。
将灰色矩形视为我的页面。 将绿色多边形视为我实际绘制的东西。
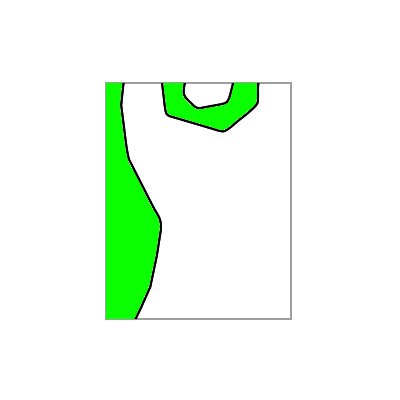
第一张图片向您展示了我实际拥有的东西,而第二张图片向您展示了我想要的最终结果。
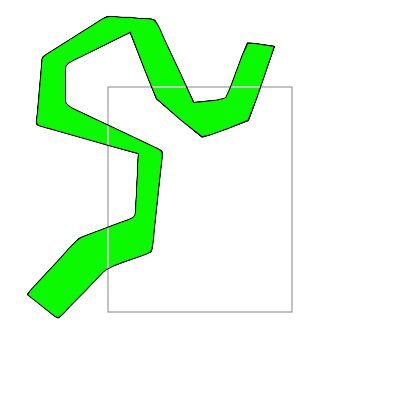
 首先,我想将多边形缩小为简单的三角形,以便仅在显示限制内绘制点。但我认为存在一个更简单的解决方案......如果你有它,请毫不犹豫地与我分享:)
首先,我想将多边形缩小为简单的三角形,以便仅在显示限制内绘制点。但我认为存在一个更简单的解决方案......如果你有它,请毫不犹豫地与我分享:)
编辑:
我也有这个棘手的情况要处理:

谢谢。
today I have a (simple) rendering problem for you. My current project gets datas from a file to generate a SVG file. Drawing things as polygon is pretty easy thanks to the SVG format, but I have a single problem: some of my polygons are in AND out of the page (meaning that some parts of them are displayed while the rest is not shown due to the fact they are out of the display limit). In order to optimize the final SVG file I need to reduce my polygon to a simpler form.
Consider the grey rectangle as my page.
Consider the green polygon as the thing I actually draw.
First picture shows you the thing that I actually have while the second picture shows you the final result I want to have.


First I thought to reduce my polygon in simple triangles in order to only draw points in the display limits. But I think a simpler solution exists... if you have it do not hesitate to share it with me :)
EDIT:
I have this tricky case to handle as well :
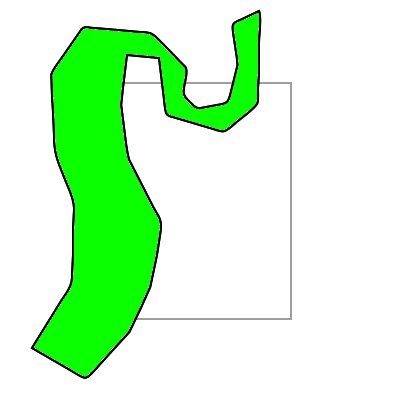

Thank you.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(1)
考虑到您的线条是垂直的还是水平的,最后一个问题非常简单。够了吗?
The last problem is pretty easy, considering that your lines are vertical or horizontal. Is that enough?