二项堆和二项式堆有什么区别?
我需要知道二项式堆和二项式堆之间的主要区别,无论它们的结构差异如何,二项式堆只能有两个子项(树表示),而二项式堆可以有任意数量的子项。
我实际上只是想知道,以第一个子节点在一个节点上、第二个子节点上有两个节点、第三个子节点上有四个节点、依此类推的方式组织二项式树结构有什么特别之处?
如果我们使用一些普通的树作为堆而不限制两个子堆,然后应用并集过程并使一个堆成为其他堆的左子堆,会怎么样?
I need to know the main difference between binary and binomial heaps regardless of the their structure difference that binary heaps can have only two child (tree representation) and binomial heaps can have any number of children.
I am actually just wondering that what so special in organizing the binomial tree structure in such a way that the first child have on one node second have two third have four and so on?
What if, if we use some normal tree for heaps without restriction of two child and then apply the union procedure and just make one heap the left child of the other heaps?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(3)
二项堆和二项式堆之间的主要区别在于堆的结构方式。在二叉堆中,堆是一棵单树,也就是一棵完全二叉树。在二项式堆中,堆是较小树的集合(即树的森林),其中每个树都是一棵二项式树。可以构建一个完整二叉树来容纳任意数量的元素,但某个阶 n 的二项式树中的元素数量始终 2n。因此,我们只需要一棵完整二叉树来支持二叉堆,但我们可能需要多个二项式树来支持二项式堆。有趣的是,二项式堆中使用的二项式树的顺序对应于森林中元素数量的二进制表示中设置的 1 位。
按原样组织二项式堆的原因是 n 阶二项式树中始终恰好有 2n 个节点。这使我们能够对二项式树中的元素数量做出假设,而无需实际检查该树的结构。另一方面,高度为 h 的完整二叉树可能具有可变数量的节点,具体取决于最后一行的填充方式。每个子节点必须具有非常精确定义的结构这一事实也可以用来证明子节点的数量最多为 O(log n),其中 n 是堆中节点的总数,这意味着一次delete-min的成本并不算太大。
这背后的一个重要细节是二项式堆不是任何碰巧有 k 个子节点的树。它是一棵严格定义为
(从技术上讲,这里不需要 0 阶特殊情况)。您可以在这里看到:
请注意,每个阶恰好有一棵树,节点的数量或位置完全没有灵活性。
然而,一个重要的替代定义如下:
(花点时间看看为什么它们是等价的)。使用第二个定义,可以快速归纳证明树中的节点数为 2n。作为基本情况,0 阶树根据需要具有 20 = 1 个节点。对于归纳步骤,如果我们有两棵 n - 1 阶树,它们总共有 2n-1 + 2n-1 = 2n节点。因此,n 阶二项式树中的节点总数恰好是 2n。
您在最后一段中描述的堆的想法并不总是能带来高效的运行时。特别是,如果您的树具有巨大的分支因子并且没有其他结构约束,那么理论上您可以构建一个由 n 个节点组成的堆,其中包含一个具有 (n - 1) 个子节点的节点。在这种情况下,从堆中删除最小元素后,您必须查看所有 n - 1 个子元素以确定哪个是新的最小值,运行时间为 O(n)。树上的其他结构约束(例如完全二叉树、二项式树等)保证了这种最坏情况不会发生。
希望这有帮助!
The key difference between a binary heap and a binomial heap is how the heaps are structured. In a binary heap, the heap is a single tree, which is a complete binary tree. In a binomial heap, the heap is a collection of smaller trees (that is, a forest of trees), each of which is a binomial tree. A complete binary tree can be built to hold any number of elements, but the number of elements in a binomial tree of some order n is always 2n. Consequently, we only need one complete binary tree to back a binary heap, but we may need multiple binomial trees to back a binomial heap. Interestingly, the orders of the binomial trees used in a binomial heap correspond to the 1 bits set in the binary representation of the number of elements in the forest.
The reason for organizing binomial heaps as they are is that a binomial tree of order n always has exactly 2n nodes in it. This allows us to make assumptions about the number of elements in the binomial tree without actually having to inspect the structure of that tree. On the other hand, a complete binary tree of some height h may have a variable number of nodes in it depending on how the last row is filled out. The fact that each of the children must have a very precisely-defined structure can also be used to prove that the number of children is at most O(log n), where n is the total number of nodes in the heap, which means that the cost of a delete-min is not too large.
An important detail behind this is that a binomial heap is not any tree that happens to have k children. It's a tree that's rigorously defined as
(Technically, the order 0 special case isn't necessary here). You can see this here:
Note that there is exactly one tree of each order, with no flexibility at all in the number or position of the nodes.
However, an important alternative definition is the following:
(Take a minute to see why these are equivalent). Using this second definition, it's a quick induction proof to show that the number of nodes in the tree is 2n. As a base case, a tree of order 0 has 20 = 1 nodes as required. For the inductive step, if we have two trees of order n - 1, they collectively have 2n-1 + 2n-1 = 2n nodes as required. Thus the total number of nodes in a binomial tree of order n is exactly 2n.
The idea for a heap that you're describing in your final paragraph does not always lead to an efficient runtime. In particular, if you have trees with a huge branching factor and no other structural constraints, then you could in theory build a heap of n nodes consisting of a single node with (n - 1) children. In that case, after deleting the minimum element from the heap, you'd have to look at all n - 1 children to determine which was the new minimum, giving a runtime of O(n). The other structural constraints on trees like complete binary trees, binomial trees, etc. guarantee that this worst-case doesn't happen.
Hope this helps!
添加上面 templatetypedef 提供的很好的答案。这是一个可视化表格,显示不同操作的不同时间复杂度
我从 普林斯顿讲座幻灯片
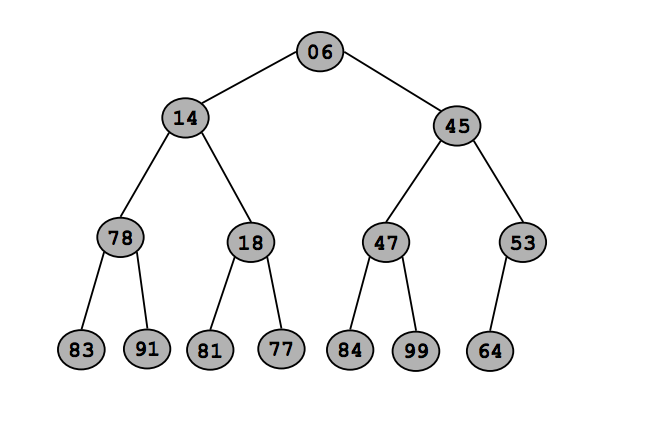
二叉堆:(几乎完全二叉树)
二项式堆:
add on to great answer above provided by templatetypedef. Here is a visual table to show different time complexity on different operations
I got this image from the Princeton lecture slides
Binary Heap: (almost complete binary tree)

Binomial Heap:
可以通过将任意两个相同秩的子满二叉树连接到根节点来创建二叉堆。这是一棵有点自由风格的树 - 可以从右侧切下一些叶子。
N 阶的二项式树不是树木的森林。它是一个根节点,连接到等级为 N-1、N-2、...、1、0 的二项式树。二项式堆是一棵结构绝对固定的树。
(恐怕有人以错误的方式阅读了 Wiki。)
k 阶二项式树有一个根节点,其子节点是 k−1, k− 阶二项式树的根2, ..., 2, 1, 0(按此顺序)。
A binary heap can be created by jointing of any two child full binary trees of the same rank onto the root node. It is a tree with a bit free style - some leaves can be cut from the right
A binomial tree of rank N is not a forest of trees. It is a root node with connected to it binomial trees of rank N-1, N-2,...,1,0. Binomial heap is a tree with absolutely fixed structure.
(I am afraid, somebody had read Wiki in a wrong way.)
A binomial tree of order k has a root node whose children are roots of binomial trees of orders k−1, k−2, ..., 2, 1, 0 (in this order).