计算非凸多边形上地理坐标的面积

Question

我想计算从 GPS 轨迹获得的多边形面积。所以基本上我会在一段时间（假设 5 秒）后存储设备/用户的位置。

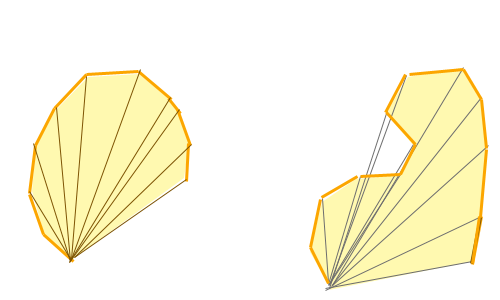
在这个轨道多边形之外，我想计算轨道所在的区域。 对于凸多边形，这不应该成为问题，因为我想我只需要计算三角形的面积（当每个三角形在第一个点中有一个起点时）。基本上如左图所示。 （黄色多边形是由 GPS 位置组成的多边形，黑线显示用于面积计算的三角形，浅黄色是所需的区域）

但昨晚我发现了这个想法的反面，即多边形不是凸的。不仅会在该区域中计算多边形外部（左上侧）的部分，还会多次测量多边形的某些区域（查看左下角的重叠三角形）。

有人知道我如何实现这一目标吗？我的意思是，如果我的多边形是 S 形的，仍然很难知道应该计算哪个面积......（但我可以忍受......只要它在（几乎）多边形上得到足够公平的结果 如果多边形是非凸的，那么

我计算多边形的凸包然后进行面积计算的另一个想法也不会很好地工作，但就像在中一样。正确的图像，如果有人能帮助我，我会计算出比实际更大的面积

，谢谢！

Answer 1

您可能会看一下多边形面积的一般公式：http://mathworld.wolfram.com/PolygonArea.html 。这也涵盖了非凸多边形的情况（只要它们不自相交）。

Answer 2

我一直这样做，但我不知道算法，因为我使用像 GEOS 这样的库C/C++、Java 中的 JTS 或 Shapely 在 Python 中。

如果您有能力承担额外的依赖项，我强烈推荐它，因为计算很强大，经过测试，采用开放标准输入格式（众所周知的文本）并处理奇怪和不寻常的几何形状（例如带孔的多边形等）。一旦你掌握了这个功能，你就可以用几何做各种奇怪而奇妙的事情。

Answer 3

有点晚了，但我只是用 Java 实现了 GPS 坐标。您必须按照此处所述标准化 GPS 坐标： 使用笛卡尔空间和世界文件生成的纬度和经度计算多边形面积。效果很好，但存在约 0.005% 的误差范围，因为笛卡尔坐标是基于理想地球半径的近似值。请注意，下面的代码假设 geojson 样式 [经度，纬度] 对，而不是相反。

public static double area(double[][] polygon) {
    Validate.isTrue(polygon.length > 3,"polygon should have at least three elements");

    double total=0;
    double[] previous=polygon[0];

    double[] center = polygonCenter(polygon);
    double xRef=center[0];
    double yRef=center[1];


    for(int i=1; i< polygon.length;i++) {
        double[] current = polygon[i];
        // convert to cartesian coordinates in meters, note this not very exact
        double x1 = ((previous[0]-xRef)*( 6378137*PI/180 ))*Math.cos( yRef*PI/180 );
        double y1 = (previous[1]-yRef)*( Math.toRadians( 6378137 ) );
        double x2 = ((current[0]-xRef)*( 6378137*PI/180 ))*Math.cos( yRef*PI/180 );
        double y2 = (current[1]-yRef)*( Math.toRadians( 6378137 ) );

        // calculate crossproduct
        total += x1*y2 - x2*y1;
        previous=current;
    }

    return 0.5 * Math.abs(total);
}

Answer 4

您想要查看空间填充曲线，例如 z 曲线或希尔伯特曲线。 sfc 曲线将表面细分为许多图块，并将 2 维问题简化为 1 维问题。您想要搜索 Nick 关于空间索引希尔伯特曲线和四叉树的博客。