具有相同簇大小的 K 均值算法变体

Question

我正在寻找最快的算法，用于按距离将地图上的点分组为大小相等的组。 k-means 聚类算法 看起来简单且有前途，但不能产生同等大小的组。

该算法是否有一种变体，或者是否有一种不同的算法可以允许所有集群的成员数量相等？

另请参阅：将 k 个簇中的 n 个点分组为相等尺寸

Answer 1

这可能会起作用：应用 Lloyd 算法 来获取 k质心。按数组中相关簇的大小降序对质心进行排序。对于i = 1到k-1，将簇i中的数据点推送到任何其他质心j (i <j ≤ k) 到 j 并重新计算质心 i< /em> （但不要重新计算簇）直到簇大小达到n / k。

此后处理步骤的复杂度为 O(k² n lg n)。

Answer 2

以防万一有人想在这里复制并粘贴一个简短的函数 - 基本上运行 KMeans，然后在分配给集群的最大点（集群大小）的约束下找到点与集群的最小匹配

from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
from scipy.optimize import linear_sum_assignment
import numpy as np


def get_even_clusters(X, cluster_size):
    n_clusters = int(np.ceil(len(X)/cluster_size))
    kmeans = KMeans(n_clusters)
    kmeans.fit(X)
    centers = kmeans.cluster_centers_
    centers = centers.reshape(-1, 1, X.shape[-1]).repeat(cluster_size, 1).reshape(-1, X.shape[-1])
    distance_matrix = cdist(X, centers)
    clusters = linear_sum_assignment(distance_matrix)[1]//cluster_size
    return clusters

Answer 3

ELKI 数据挖掘框架有一个 等大小 k 均值教程。

这不是一个特别的算法，但它是一个足够简单的 k 均值变体，可以编写教程并教人们如何实现自己的聚类算法变体；显然，有些人确实需要他们的簇具有相同的大小，尽管 SSQ 质量会比常规 k 均值差。

在 ELKI 0.7.5 中，您可以选择此算法为 tutorial.clustering.SameSizeKMeansAlgorithm。

Answer 4

一般来说，按照距离将地图上的点分成大小相等的组在理论上是一项不可能完成的任务。因为将点分组为大小相等的组与按距离将点分组为簇相冲突。

看这个情节：

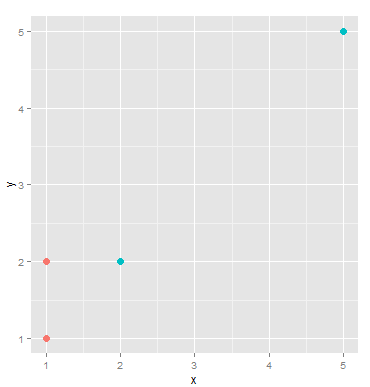
有四个点：

A.[1,1]
B.[1,2]
C.[2,2]
D.[5,5]

如果我们将这些点聚类为两个簇。显然，(A,B,C) 将是聚类 1，D 将是聚类 2。但如果我们需要相同大小的组，则 (A,B) 将是一个聚类，(C,D) 将是另一个聚类。这违反了聚类规则，因为 C 更接近 (A,B) 的中心，但它属于聚类 (C,D)。因此不能同时满足集群和同等大小的组的要求。

Answer 5

您可以将距离视为定义加权图。相当多的图划分算法明确地基于尝试将图顶点划分为两个大小相等的集合。例如，这出现在 Kernighan-Lin 算法 和 < a href="http://www.stanford.edu/~dgleich/demos/matlab/spectral/spectral.html#recursive" rel="noreferrer">使用拉普拉斯算子的谱图划分。要获得多个簇，可以递归地应用分区算法；在光谱图分区的链接上对此有一个很好的讨论。

Answer 6

尝试这个 k-means 变体：

初始化：

• 从数据集中随机选择 k 个中心，或者更好的是
• 对每个点使用 kmeans++ 策略，计算到其最近的聚类中心的距离，并为此
• 从堆中绘制点构建一个堆，并将它们分配给最近的簇，除非簇已经满了。如果是这样，计算下一个最近的簇中心并重新插入堆中

最后，您应该有一个分区，满足每个簇+-1相同数量的对象的要求（确保最后几个簇也有正确的数量）前 m 个簇应具有 ceil 对象，其余的恰好是 floor 对象。）

迭代步骤：

必备条件：每个集群的列表，其中包含“交换建议”（希望位于不同集群中的对象）。

E 步骤：按照常规 k 均值计算更新的聚类中心

M 步骤：迭代所有点（可以是一个点，也可以是一批中的所有点）

计算最近的聚类中心到比当前聚类更接近的对象/所有聚类中心。如果是不同的簇：

• 如果另一个簇比当前簇小，则将其移动到新簇
• 如果有来自另一个簇（或任何距离更小的簇）的交换提议，则交换两个元素簇分配（如果有多个提议，请选择改进最大的一个）
• ，否则，指示另一簇的交换建议

簇大小保持不变（+- ceil/floor 差异），对象仅从一个簇移动聚类到另一个，只要它能导致估计的改进。因此它应该像 k 均值那样在某个点收敛。但它可能会慢一些（即更多迭代）。

我不知道这是否已经发布或实施过。这正是我会尝试的（如果我会尝试 k-means。有更好的聚类算法。）

Answer 7

在阅读了这个问题和几个类似的问题后，我使用 https://elki-project.github.io/tutorial/same-size_k_means 它利用 scikit-learn 的 K-Means 实现来实现大多数常见方法和熟悉的 API。

我的实现可以在这里找到：
https://github.com/ndanielsen/Same-Size-K-Means

聚类逻辑在此函数中找到：_labels_inertia_precompute_dense()

Answer 8

给定簇质心，有更干净的后处理。令 N 为项目数，K 为簇数，S = ceil(N/K) 最大簇大小。

• 创建元组列表 (item_id, cluster_id, distance)
• 根据距离对元组进行排序
• 对于已排序的元组列表中的每个元素 (item_id, cluster_id, distance)：
  • 如果 cluster_id 中的元素数量超过 S 则不执行任何操作
  • 否则将 item_id 添加到集群 cluster_id。

这在 O(NK lg(N)) 中运行，应该给出与 @larsmans 解决方案相当的结果，并且更容易实现。在伪Python中

dists = []
clusts = [None] * N
counts = [0] * K

for i, v in enumerate(items):
    dist = map( lambda x: dist(x, v), centroids )
    dd = map( lambda (k, v): (i, k, v), enumerate(dist) )
    dists.extend(dd)

dists = sorted(dists, key = lambda (x,y,z): z)

for (item_id, cluster_id, d) in dists:
    if counts[cluster_id] >= S:
        continue
    if clusts[item_id] == None:
        clusts[item_id] = cluster_id
        counts[cluster_id] = counts[cluster_id] + 1

Answer 9

考虑某种形式的递归贪婪合并——每个点都以单例簇开始，并重复合并最接近的两个点，这样合并不会超过最大值。尺寸。如果您别无选择，只能超过最大大小，则在本地重新集群。这是回溯层次聚类的一种形式：http://en.wikipedia.org/wiki/Hierarchical_clustering

Answer 10

最近我自己需要这个来处理不是很大的数据集。我的答案虽然运行时间比较长，但是保证收敛到局部最优。

def eqsc(X, K=None, G=None):
    "equal-size clustering based on data exchanges between pairs of clusters"
    from scipy.spatial.distance import pdist, squareform
    from matplotlib import pyplot as plt
    from matplotlib import animation as ani    
    from matplotlib.patches import Polygon   
    from matplotlib.collections import PatchCollection
    def error(K, m, D):
        """return average distances between data in one cluster, averaged over all clusters"""
        E = 0
        for k in range(K):
            i = numpy.where(m == k)[0] # indeces of datapoints belonging to class k
            E += numpy.mean(D[numpy.meshgrid(i,i)])
        return E / K
    numpy.random.seed(0) # repeatability
    N, n = X.shape
    if G is None and K is not None:
        G = N // K # group size
    elif K is None and G is not None:
        K = N // G # number of clusters
    else:
        raise Exception('must specify either K or G')
    D = squareform(pdist(X)) # distance matrix
    m = numpy.random.permutation(N) % K # initial membership
    E = error(K, m, D)
    # visualization
    #FFMpegWriter = ani.writers['ffmpeg']
    #writer = FFMpegWriter(fps=15)
    #fig = plt.figure()
    #with writer.saving(fig, "ec.mp4", 100):
    t = 1
    while True:
        E_p = E
        for a in range(N): # systematically
            for b in range(a):
                m[a], m[b] = m[b], m[a] # exchange membership
                E_t = error(K, m, D)
                if E_t < E:
                    E = E_t
                    print("{}: {}<->{} E={}".format(t, a, b, E))
                    #plt.clf()
                    #for i in range(N):
                        #plt.text(X[i,0], X[i,1], m[i])
                    #writer.grab_frame()
                else:
                    m[a], m[b] = m[b], m[a] # put them back
        if E_p == E:
            break
        t += 1           
    fig, ax = plt.subplots()
    patches = []
    for k in range(K):
        i = numpy.where(m == k)[0] # indeces of datapoints belonging to class k
        x = X[i]        
        patches.append(Polygon(x[:,:2], True)) # how to draw this clock-wise?
        u = numpy.mean(x, 0)
        plt.text(u[0], u[1], k)
    p = PatchCollection(patches, alpha=0.5)        
    ax.add_collection(p)
    plt.show()

if __name__ == "__main__":
    N, n = 100, 2    
    X = numpy.random.rand(N, n)
    eqsc(X, G=3)

Answer 11

等大小 k 均值是约束 k 均值过程的特殊情况，其中每个簇必须具有最小数量的点。这个问题可以表述为一个图问题，其中节点是要聚类的点，每个点到每个质心都有一条边，其中边权重是到质心的欧氏距离的平方。此处讨论：

Bradley PS、Bennett KP、Demiriz A (2000)、约束 K 均值聚类。微软研究院。

Python 实现可在此处获取。

Answer 12

2012 年 1 月添加：
比后处理更好的是保持簇大小
与它们的生长大致相同。
例如，为每个 X 找到 3 个最近的中心，
然后将 X 添加到最好的那个
距离 - λ 簇大小。

---

如果 k 均值中的簇大小大致相等，则在 k 均值之后进行简单的贪婪后处理可能就足够了。
（这近似于 k-means 的 Npt x C 距离矩阵上的分配算法。）

可以迭代，

diffsizecentres = kmeans( X, centres, ... )
X_centre_distances = scipy.spatial.distance.cdist( X, diffsizecentres )
    # or just the nearest few centres
xtoc = samesizeclusters( X_centre_distances )
samesizecentres = [X[xtoc[c]].mean(axis=0) for c in range(k)]
...

如果迭代改变中心很多，我会感到惊讶，
但这取决于™。

你的 Npoint Ncluster 和 Ndim 大约有多大？

#!/usr/bin/env python
from __future__ import division
from operator import itemgetter
import numpy as np

__date__ = "2011-03-28 Mar denis"

def samesizecluster( D ):
    """ in: point-to-cluster-centre distances D, Npt x C
            e.g. from scipy.spatial.distance.cdist
        out: xtoc, X -> C, equal-size clusters
        method: sort all D, greedy
    """
        # could take only the nearest few x-to-C distances
        # add constraints to real assignment algorithm ?
    Npt, C = D.shape
    clustersize = (Npt + C - 1) // C
    xcd = list( np.ndenumerate(D) )  # ((0,0), d00), ((0,1), d01) ...
    xcd.sort( key=itemgetter(1) )
    xtoc = np.ones( Npt, int ) * -1
    nincluster = np.zeros( C, int )
    nall = 0
    for (x,c), d in xcd:
        if xtoc[x] < 0  and  nincluster[c] < clustersize:
            xtoc[x] = c
            nincluster[c] += 1
            nall += 1
            if nall >= Npt:  break
    return xtoc

#...............................................................................
if __name__ == "__main__":
    import random
    import sys
    from scipy.spatial import distance
    # http://docs.scipy.org/doc/scipy/reference/spatial.distance.html

    Npt = 100
    C = 3
    dim = 3
    seed = 1

    exec( "\n".join( sys.argv[1:] ))  # run this.py N= ...
    np.set_printoptions( 2, threshold=200, edgeitems=5, suppress=True )  # .2f
    random.seed(seed)
    np.random.seed(seed)

    X = np.random.uniform( size=(Npt,dim) )
    centres = random.sample( X, C )
    D = distance.cdist( X, centres )
    xtoc = samesizecluster( D )
    print "samesizecluster sizes:", np.bincount(xtoc)
        # Npt=100 C=3 -> 32 34 34

Answer 13

我将答案中提出的大部分算法添加到存储库 https://github.com/brand17/clusters_equal_size< /a>.

最有效的是得票最多的答案。

我开发了一些其他算法（得票最多的仍然是最好的）：

1. 我修改了迭代交换提案 - 通过识别和消除直接循环而不是仅仅交换（它提高了一点效率）

2. 我还开发了以下算法：迭代最近的质心对并通过有效移动 Voronoi 图边界来交换它们之间的点，以便点数相差不超过 1。

Answer 14

另请查看 Kd 树，它对数据进行分区，直到每个分区的成员小于 BUCKET_SIZE（算法的输入）。

这不会强制存储桶/分区的大小完全相同，但它们都会小于 BUCKET_SIZE。

Answer 15

我可以谦虚地建议您尝试这个项目 ekmeans。

Java K-means 聚类实现，具有可选的特殊相等选项，该选项对聚类应用相等基数约束，同时尽可能保持空间内聚性。

它还处于实验阶段，因此请注意已知错误。

Answer 16

我也一直在纠结如何解决这个问题。然而，我意识到我一直使用了错误的关键字。如果您希望点结果成员的数量相同，那么您正在进行分组，而不是聚类。我终于能够使用简单的 python 脚本和 postgis 查询解决问题。

例如，我有一个名为 tb_points 的表，其中有 4000 个坐标点，您想将其分为 10 个相同大小的组，每个组包含 400 个坐标点。这是表结构的示例

CREATE TABLE tb_points (
  id SERIAL PRIMARY KEY,
  outlet_id INTEGER,
  longitude FLOAT,
  latitide FLOAT,
  group_id INTEGER
);

那么您需要做的是：

1. 找到将作为您的起点的第一个坐标
2. 查找距离您的起点最近的坐标，按距离升序排列，按您首选成员的数量限制结果（在这种情况下 400)
3. 通过更新 group_id 列来更新结果
4. 对其余数据执行上述 3 个步骤 10 次，其中 group_id 列仍然为 NULL

这是 python 中的实现：

import psycopg2

dbhost = ''
dbuser = ''
dbpass = ''
dbname = ''
dbport = 5432

conn = psycopg2.connect(host = dbhost,
       user = dbuser,
       password = dbpass,
       database = dbname,
       port = dbport)

def fetch(sql):
    cursor = conn.cursor()
    rs = None
    try:
        cursor.execute(sql)
        rs = cursor.fetchall()
    except psycopg2.Error as e:
        print(e.pgerror)
        rs = 'error'
    cursor.close()
    return rs

def execScalar(sql):
    cursor = conn.cursor()
    try:
        cursor.execute(sql)
        conn.commit()
        rowsaffected = cursor.rowcount
    except psycopg2.Error as e:
        print(e.pgerror)
        rowsaffected = -1
        conn.rollback()
    cursor.close()
    return rowsaffected


def select_first_cluster_id():
    sql = """ SELECT a.outlet_id as ori_id, a.longitude as ori_lon,
    a.latitude as ori_lat, b.outlet_id as dest_id, b.longitude as
    dest_lon, b.latitude as dest_lat,
    ST_Distance(CAST(ST_SetSRID(ST_Point(a.longitude,a.latitude),4326)
    AS geography), 
    CAST(ST_SetSRID(ST_Point(b.longitude,b.latitude),4326) AS geography))
    AS air_distance FROM  tb_points a CROSS JOIN tb_points b WHERE
    a.outlet_id != b.outlet_id and a.group_id is NULL and b.group_id is
    null order by air_distance desc limit 1 """
    return sql

def update_group_id(group_id, ori_id, limit_constraint):
    sql = """ UPDATE tb_points
    set group_id = %s
    where outlet_id in
    (select b.outlet_id
    from tb_points a,
    tb_points b
    where a.outlet_id = '%s'
    and a.group_id is null
    and b.group_id is null
    order by ST_Distance(CAST(ST_SetSRID(ST_Point(a.longitude,a.latitude),4326) AS geography),
    CAST(ST_SetSRID(ST_Point(b.longitude,b.latitude),4326) AS geography)) asc
    limit %s)
    """ % (group_id, ori_id, limit_constraint)
    return sql

def clustering():
    data_constraint = [100]
    n = 1
    while n <= 10:
        sql = select_first_cluster_id()
        res = fetch(sql)
        ori_id = res[0][0]

        sql = update_group_id(n, ori_id, data_constraint[0])
        print(sql)
        execScalar(sql)

        n += 1

clustering()

希望它有帮助

Answer 17

在簇分配过程中，我们还可以在距离上添加“频率惩罚”，这使得高频簇更难获得额外的分数。这在“频率敏感竞争学习”中进行了描述
高维超球面的平衡聚类 - Arindam Banerjee 和 Joydeep Ghosh - IEEE Transactions on Neural Networks"

http://www.ideal.ece.utexas.edu/papers/arindam04tnn.pdf

他们还有在线/流媒体版本。

Answer 18

您想要查看空间填充曲线，例如 z 曲线或希尔伯特曲线。您可以考虑一条空间填充曲线，将二维问题简化为一维问题。尽管 sfc 索引只是二维数据的重新排序，而不是数据的完美聚类，但当解决方案不能满足完美聚类并且必须相当快地计算时，它可能很有用。