关于广度优先完整性与深度优先不完整性的问题
根据诺维格在 AIMA(人工智能:一种现代方法)中的说法,深度优先算法并不完整(不会总是产生解决方案),因为在某些情况下,下降的子树将是无限的。
另一方面,如果分支因子不是无限的,则广度优先方法被认为是完整的。但这与 DFS 中子树无限的情况不是有些相同的“事情”吗?
如果树的深度是有限的,那么DFS就不能说是完备的吗?那么为什么 BFS 是完备的而 DFS 不是,因为 BFS 的完备性依赖于分支因子是有限的!
According to Norvig in AIMA (Artificial Intelligence: A modern approach), the Depth-first algorithm is not complete (will not always produce a solution) because there are cases when the subtree being descended will be infinite.
On the other hand, the Breadth-first approach is said to be complete if the branching factor is not infinite. But isn't that somewhat the same "thing" as in the case of the subtree being infinite in DFS?
Can't the DFS be said to be complete if the tree's depth is finite? How is then that the BFS is complete and the DFS is not, since the completeness of the BFS relies on the branching factor being finite!
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(3)
一棵树可以是无限的,而不具有无限的分支因子。作为示例,请考虑魔方的状态树。给定立方体的配置,移动的次数是有限的(我相信是 18 次,因为一次移动包括选取 9 个“平面”之一并将其沿两个可能的方向之一旋转)。然而,树是无限深的,因为完全有可能仅来回交替旋转同一平面(永远不会取得任何进展)。为了防止 DFS 这样做,通常会缓存所有访问过的状态(有效地修剪状态树)——正如您可能知道的那样。但是,如果状态空间太大(或实际上无限),这将无济于事。
我没有广泛研究过人工智能,但我认为说 BFS 完备而 DFS 不完备(完备性毕竟只是一个在某处定义的术语)的理由是,无限深的树比无限深的树出现得更频繁。分支因子(因为具有无限分支因子意味着您有无限数量的选择,我认为这并不常见 - 游戏和模拟通常是离散的)。即使对于有限树,BFS 通常也会表现得更好,因为 DFS 很可能从错误的路径开始,在达到目标之前探索树的大部分。尽管如此,正如您所指出的,在有限树中,DFS 将最终找到解决方案(如果存在)。
A tree can be infinite without having an infinite branching factor. As an example, consider the state tree for Rubik's Cube. Given a configuration of the cube, there is a finite number of moves (18, I believe, since a move consists of picking one of the 9 "planes" and rotating it in one of the two possible directions). However, the tree is infinitely deep, since it is perfectly possible to e.g. only rotate the same plane alternatingly back and forth (never making any progress). In order to prevent a DFS from doing this, one normally caches all the visited states (effectively pruning the state tree) - as you probably know. However, if the state space is too large (or actually infinite), this won't help.
I have not studied AI extensively, but I assume that the rationale for saying that BFS is complete while DFS is not (completeness is, after all, just a term that is defined somewhere) is that infinitely deep trees occur more frequently than trees with infinite branching factors (since having an infinite branching factor means that you have an infinite number of choices, which I believe is not common - games and simulations are usually discrete). Even for finite trees, BFS will normally perform better because DFS is very likely to start out on a wrong path, exploring a large portion of the tree before reaching the goal. Still, as you point out, in a finite tree, DFS will eventually find the solution if it exists.
DFS 不能陷入循环(如果我们有打开和关闭状态的列表)。该算法并不完整,因为它无法在无限空间中找到解,即使解的深度
d远低于无穷大。想象一个奇怪定义的状态空间,其中每个节点具有与斐波那契序列中的以下数字相同数量的后继者。因此,它是递归定义的,因此是无限的。我们正在寻找节点 2(图中标记为绿色)。如果 DFS 从树的右分支开始,它将需要无数的步骤来验证我们的节点不在那里。因此它并不完整(它不会在合理的时间内完成)。 BFS 将在第 3 次迭代中找到解决方案。
魔方状态空间是有限的,它很大,但是有限(人类陷入循环但DFS 不会重复相同的动作两次)。 DFS会找到非常低效的方法来解决它,有时这种解决方案是不可行的。通常我们认为最大深度是无限的,但我们的资源(内存)始终是有限的。
DFS can not stuck in cycles (if we have a list of opened and closed states). The algorithm is not complete since it does not find a solution in an infinite space, even though the solution is in depth
dwhich is much lower than infinity.Imagine a strangely defined state space where each node has same number of successors as following number in Fibonacci sequence. So, it's recursively defined and therefore infinite. We're looking for node 2 (marked green in the graph). If DFS starts with the right branch of tree, it will take infinite number of steps to verify that our node is not there. Therefore it's not complete (it won't finish in reasonable time). BFS would find the solution in 3rd iteration.
Rubik's cube state space is finite, it is huge, but finite (human stuck in cycles but DFS won't repeat the same move twice). DFS would find very inefficient way how to solve it, sometimes this kind of solution is infeasible. Usually we consider maximum depth infinite, but our resources (memory) are always finite.
深度优先搜索的属性在很大程度上取决于图搜索还是
使用树搜索版本。图搜索版本,避免重复状态和冗余
路径,在有限状态空间中是完整的,因为它最终会扩展每个节点。
另一方面,树搜索版本并不完整,例如,在图 3.6 中
算法将永远遵循 Arad–Sibiu–Arad–Sibiu 循环
来源:人工智能:现代方法
The properties of depth-first search depend strongly on whether the graph-search or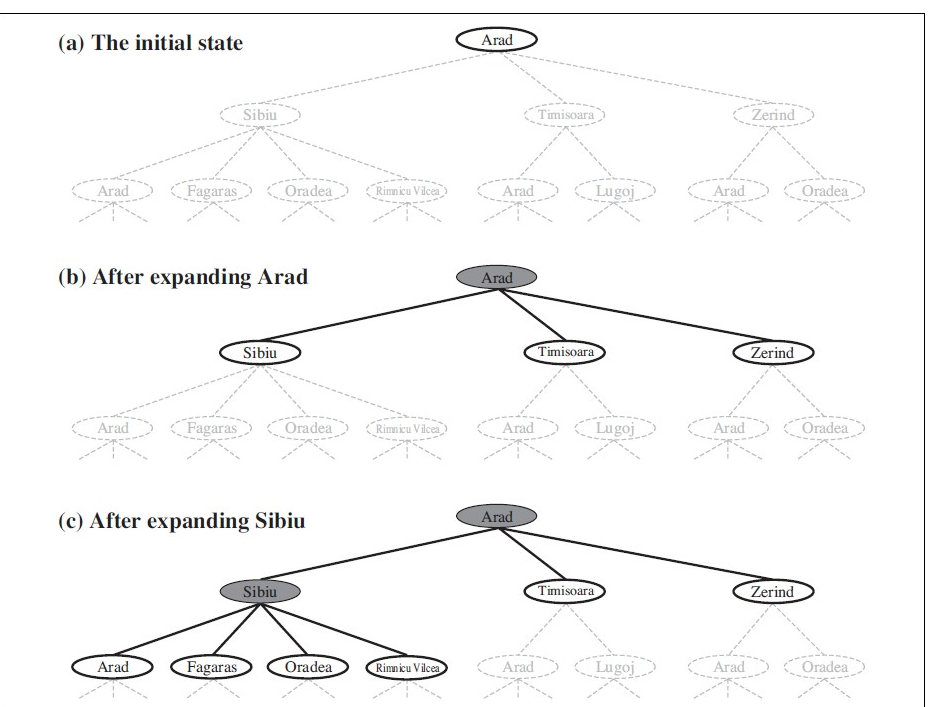
tree-search version is used. The graph-search version, which avoids repeated states and redundant
paths, is complete in finite state spaces because it will eventually expand every node.
The tree-search version, on the other hand, is not complete—for example, in Figure 3.6 the
algorithm will follow the Arad–Sibiu–Arad–Sibiu loop forever
Source: AI: a modern approach