简介
作为一个较大程序的一部分（与体积图形的渲染相关），我有一个小但棘手的子问题，其中需要以特定方式标记任意（但有限）三角形 2D 网格。不久前，我编写了一个解决方案（见下文），该解决方案对于我当时拥有的测试网格来说已经足够好了，尽管我意识到该方法可能无法很好地适用于人们能想到的每种可能的网格。现在我终于遇到了一个网格，当前的解决方案根本无法表现得那么好 - 看起来我应该想出一种完全不同的方法。不幸的是，似乎我真的无法重新调整我的思路，这就是为什么我想在这里问。
问题
请考虑下图。 （颜色不是问题的一部分；我只是添加它们来改进（？）可视化。此外，变化的边缘宽度是完全不相关的工件。）
对于每个三角形（例如，橙色 ABC 和绿色 ABD），三个边中的每一个都需要指定两个标签之一，例如“0”或“1”。只有两个要求：
- 三角形的所有边不能有相同的标签。换句话说，对于每个三角形，必须有两个“0”和一个“1”，或两个“1”和一个“0”。
- 如果一条边由两个三角形共享，则两个三角形必须具有相同的标签。换句话说，如果图片中的边AB对于三角形ABC被标记为“0”，那么它对于ABD也必须被标记为“0”。
该网格是真正的 2D 网格，并且它是有限的：即，它不环绕，并且具有明确定义的外边界。显然，在边界上满足要求相当容易，但在内部却变得更加困难。
直觉上，看起来至少应该存在一个解决方案，尽管我无法证明这一点。 （通常有几个——任何一个就足够了。）
当前的解决方案
我当前的解决方案是一个非常强力的解决方案（此处提供只是为了完整性——随意跳过本节）：
- 维护四组三角形——一组对应剩余待标记边的可能计数 (0..3)。一开始，每个三角形都在需要标记三个边的集合中。
- 只要存在带有未标记边的三角形：
找到仍留有三角形的最小非零数量的未分配边。换句话说：在任何给定时间，我们都尝试最小化已部分完成标签的三角形数量。剩余的边数将为 1 到 3 之间的任何值。然后，只需选择一个这样的三角形，其中剩余的特定边数将被分配。对于这个三角形，执行以下操作：
- 查看任何剩余边的标签是否已由其他三角形的标签强加。如果是这样，请按照上面的要求 #2 所暗示的分配标签。
- 如果这导致死胡同（即当前三角形无法再满足要求#1），则从头开始整个过程。
- 按如下方式分配任何剩余边：
- 如果到目前为止还没有标记边，则随机分配第一个边。
- 当一条边已分配时，分配第二条边，以便它具有相反的标签。
- 分配两条边时：如果它们具有相同的标签，则将第三条边分配为具有相反的标签（显然）；如果两个标签不同，则随机分配第三个标签。
- 针对不同数量的未分配边更新三角形集。
- 如果我们到达这里，那么我们就有了一个解决方案——万岁！
通常这种方法只需几次迭代即可找到解决方案，但最近我遇到了一个网格，该网格的算法往往仅在重试一两千次后才会终止...这显然表明可能存在是它永远不会终止的网格。
现在，我希望有一个确定性算法，保证总能找到解决方案。计算复杂性并不是一个大问题，因为网格不是很大，并且标记基本上只需要在加载新网格时完成，而这种情况不会一直发生——因此具有（例如）指数的算法只要有效，复杂性就应该没问题。 （当然：效率越高越好。）
感谢您阅读本文。现在，任何帮助将不胜感激！
编辑：基于建议解决方案的结果
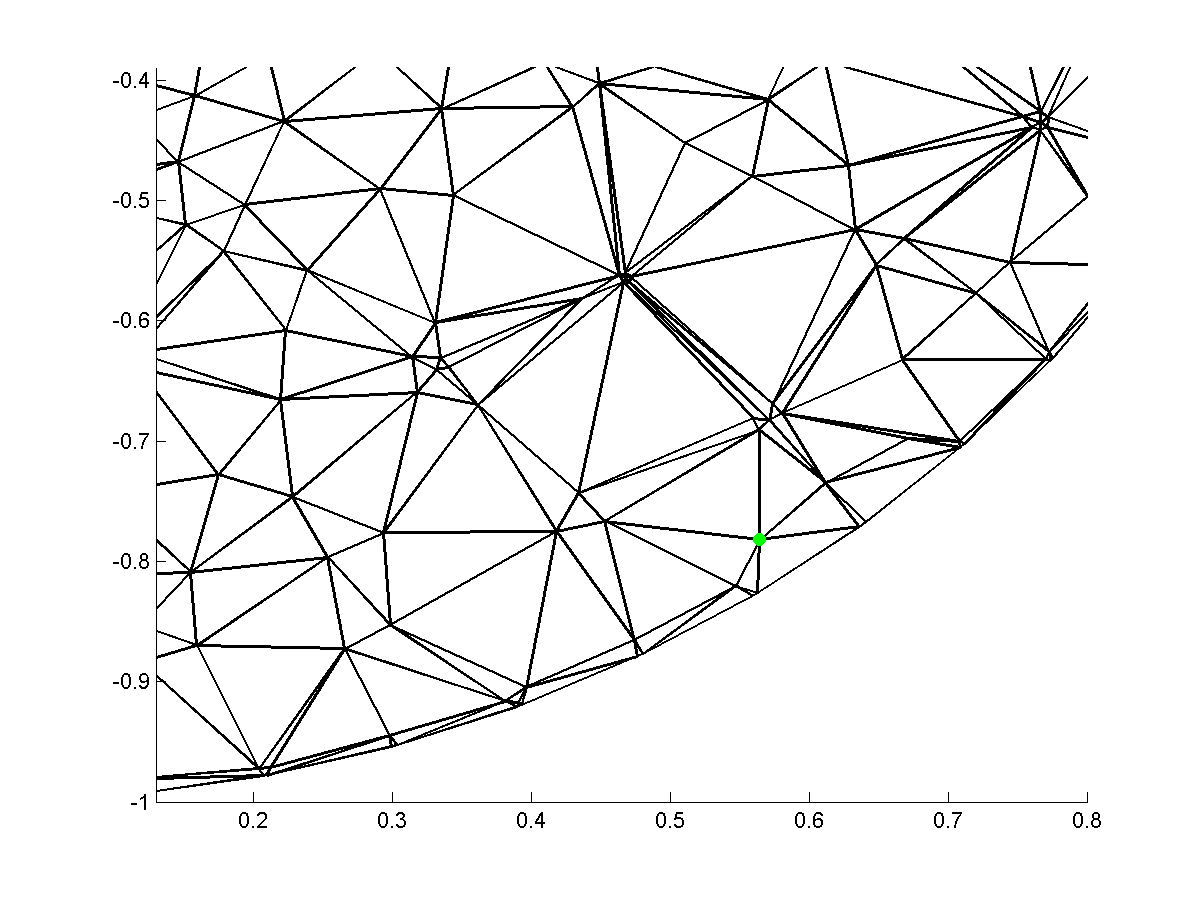
不幸的是，我无法获得 辩证法建议的方法起作用。也许我没有得到正确的结果......无论如何，考虑以下网格，其起点由绿点表示：
让我们放大一点......
现在，让我们开始算法。第一步之后，标签如下所示（红色=“星号路径”，蓝色=“环线路径”）：
到目前为止，一切都很好。第二步之后：
第三个：
... 第四：
但现在我们有一个问题！让我们再进行一轮 - 但请注意洋红色绘制的三角形：
根据我当前的实现，洋红色三角形的所有边缘都在环形路径上，因此它们应该是蓝色的——这实际上使其成为一个反例。现在也许我以某种方式弄错了......但无论如何，最接近起始节点的两条边显然不能是红色的；如果第三个被标记为红色，那么似乎该解决方案不再真正符合这个想法。
顺便说一句，这是使用的数据。每行代表一条边，列的解释如下：
- 第一个节点的
- 索引 第二个节点的索引
- x 第一个节点的坐标
- y 第一个节点的坐标
- x 第二个节点的坐标
- y 第二个节点的坐标
起始节点是索引为 1 的节点。
我想接下来我应该尝试 Rafał Dowgird 建议的方法...但也许我应该做一些完全不同的事情一会儿:)
Introduction
As part of a larger program (related to rendering of volumetric graphics), I have a small but tricky subproblem where an arbitrary (but finite) triangular 2D mesh needs to be labeled in a specific way. Already a while ago I wrote a solution (see below) which was good enough for the test meshes I had at the time, even though I realized that the approach will probably not work very well for every possible mesh that one could think of. Now I have finally encountered a mesh for which the present solution does not perform that well at all -- and it looks like I should come up with a totally different kind of an approach. Unfortunately, it seems that I am not really able to reset my lines of thinking, which is why I thought I'd ask here.
The problem
Consider the picture below. (The colors are not part of the problem; I just added them to improve (?) the visualization. Also the varying edge width is a totally irrelevant artifact.)
For every triangle (e.g., the orange ABC and the green ABD), each of the three edges needs to be given one of two labels, say "0" or "1". There are just two requirements:
- Not all the edges of a triangle can have the same label. In other words, for every triangle there must be two "0"s and one "1", or two "1"s and one "0".
- If an edge is shared by two triangles, it must have the same label for both. In other words, if the edge AB in the picture is labeled "0" for the triangle ABC, it must be labeled "0" for ABD, too.
The mesh is a genuine 2D one, and it is finite: i.e., it does not wrap, and it has a well-defined outer border. Obviously, on the border it is quite easy to satisfy the requirements -- but it gets more difficult inside.
Intuitively, it looks like at least one solution should always exist, even though I cannot prove it. (Usually there are several -- any one of them is enough.)
Current solution
My current solution is a really brute-force one (provided here just for completeness -- feel free to skip this section):
- Maintain four sets of triangles -- one for each possible count (0..3) of edges remaining to be labeled. In the beginning, every triangle is in the set where three edges remain to be labeled.
- For as long as there are triangles with non-labeled edges:
Find the smallest non-zero number of unallocated edges for which there are still triangles left. In other words: at any given time, we try to minimize the number of triangles for which the labeling has been partially completed. The number of edges remaining will be anything between 1 and 3. Then, just pick one such triangle with this specific number of edges remaining to be allocated. For this triangle, do the following:
- See if the labeling of any remaining edge is already imposed by the labeling of some other triangle. If so, assign the labels as implied by requirement #2 above.
- If this results in a dead end (i.e., requirement #1 can no more be satisfied for the present triangle), then start over the whole process from the very beginning.
- Allocate any remaining edges as follows:
- If no edges have been labeled so far, assign the first one randomly.
- When one edge already allocated, assign the second one so that it will have the opposite label.
- When two edges allocated: if they have the same label, assign the third one to have the opposite label (obviously); if the two have different labels, assign the third one randomly.
- Update the sets of triangles for the different counts of unallocated edges.
- If we ever get here, then we have a solution -- hooray!
Usually this approach finds a solution within just a couple of iterations, but recently I encountered a mesh for which the algorithm tends to terminate only after one or two thousands of retries... Which obviously suggests that there may be meshes for which it never terminates.
Now, I would love to have a deterministic algorithm that is guaranteed to always find a solution. Computational complexity is not that big an issue, because the meshes are not very large and the labeling basically only has to be done when a new mesh is loaded, which does not happen all the time -- so an algorithm with (for example) exponential complexity ought to be fine, as long as it works. (But of course: the more efficient, the better.)
Thank you for reading this far. Now, any help would be greatly appreciated!
Edit: Results based on suggested solutions
Unfortunately, I cannot get the approach suggested by Dialecticus to work. Maybe I did not get it right... Anyway, consider the following mesh, with the start point indicated by a green dot:
Let's zoom in a little bit...
Now, let's start the algorithm. After the first step, the labeling looks like this (red = "starred paths", blue = "ringed paths"):
So far so good. After the second step:
And the third:
... fourth:
But now we have a problem! Let's do one more round - but please pay attention on the triangle plotted in magenta:
According to my current implementation, all the edges of the magenta triangle are on a ring path, so they should be blue -- which effectively makes this a counterexample. Now maybe I got it wrong somehow... But in any case the two edges that are nearest to the start node obviously cannot be red; and if the third one is labeled red, then it seems that the solution does not really fit the idea anymore.
Btw, here is the data used. Each row represents one edge, and the columns are to be interpreted as follows:
- Index of first node
- Index of second node
- x coordinate of first node
- y coordinate of first node
- x coordinate of second node
- y coordinate of second node
The start node is the one having index 1.
I guess that next I should try the method suggested by Rafał Dowgird... But perhaps I ought to do something completely different for a while :)
发布评论
评论（2）
如果您对三角形进行排序，使得每个三角形最多有 2 个相邻三角形按顺序排在它前面，那么您就完成了：只需按此顺序为它们着色即可。该条件保证对于每个着色的三角形，您将始终有至少一个未着色的边，您可以选择其颜色以满足条件。
这样的顺序是存在的，并且可以通过以下方式构建：
If you order the triangles so that for every triangle at most 2 of its neighbors precede it in the order, then you are set: just color them in this order. The condition guarantees that for each triangle being colored you will always have at least one uncolored edge whose color you can choose so that the condition is satisfied.
Such an order exists and can be constructed the following way:
给定网格中的任何节点，网格都可以被视为围绕该节点的一组同心环（如蜘蛛网）。将不在环中的所有边（带星号的路径）的值指定为 0，并将环中的所有边（带星号的路径）的值指定为 1。我无法证明这一点，但我确信您会的获得正确的标签。每个三角形都有一条边是某个环的一部分。
Given any node in the mesh the mesh can be viewed as set of concentric rings around this node (like spider's web). Give all edges that are not in the ring (starred paths) a value of 0, and give all edges that are in the ring (ringed paths) a value of 1. I can't prove it, but I'm certain you will get the correct labeling. Every triangle will have exactly one edge that is part of some ring.