当前位置：文江博客话题详情

用于计算百分位数以消除异常值的快速算法

发布于 2024-09-24 08:00:25 字数 2824 浏览 5 评论 0原文

我有一个程序需要重复计算数据集的近似百分位（顺序统计），以便在进一步处理之前删除异常值。我目前正在通过对值数组进行排序并选择适当的元素来实现此目的；这是可行的，但尽管它只是该程序的一小部分，但它在配置文件上是一个明显的亮点。

更多信息：

该数据集包含最多 100000 个浮点数，并假设“合理”分布 - 不太可能出现重复，也不太可能在特定值附近出现密度大幅峰值；如果由于某种奇怪的原因，分布是奇怪的，那么近似值不太准确是可以接受的，因为无论如何数据都可能被搞乱并且进一步的处理是可疑的。然而，数据不一定是均匀或正态分布的；它只是不太可能退化。
一个近似的解决方案就可以了，但我确实需要了解近似值如何引入误差以确保其有效。
由于目标是消除异常值，因此我始终对相同数据计算两个百分位数：例如，一个在 95% 处，一个在 5% 处。
该应用程序使用 C# 编写，其中一些繁重的工作使用 C++ 编写；伪代码或任何一个中预先存在的库都可以。
只要合理，一种完全不同的消除异常值的方法也可以。
更新：我似乎正在寻找一个近似的选择算法。

尽管这一切都是在循环中完成的，但每次数据都（略有）不同，因此像以前那样重用数据结构并不容易对于这个问题。

已实现的解决方案

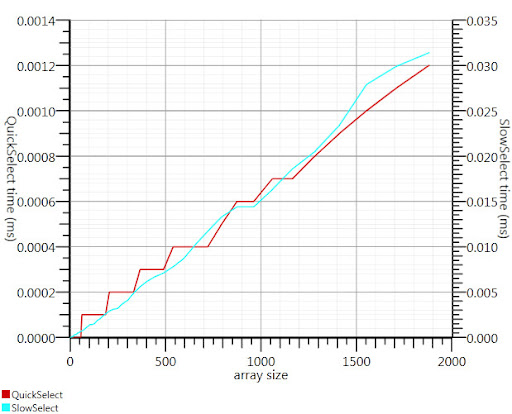
使用 Gronim 建议的 wikipedia 选择算法将这部分运行时间减少了大约 20 倍。

由于我找不到 C# 实现，所以这就是我的想法。即使对于小输入，它也比 Array.Sort 更快；当有 1000 个元素时，速度提高了 25 倍。

public static double QuickSelect(double[] list, int k) {
    return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
    while (true) {
        // Assume startI <= k < endI
        int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
        int splitI = partition(list, startI, endI, pivotI);
        if (k < splitI)
            endI = splitI;
        else if (k > splitI)
            startI = splitI + 1;
        else //if (k == splitI)
            return list[k];
    }
    //when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
    double pivotValue = list[pivotI];
    list[pivotI] = list[startI];
    list[startI] = pivotValue;

    int storeI = startI + 1;//no need to store @ pivot item, it's good already.
    //Invariant: startI < storeI <= endI
    while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
    //now storeI == endI || list[storeI] > pivotValue
    //so elem @storeI is either irrelevant or too large.
    for (int i = storeI + 1; i < endI; ++i)
        if (list[i] <= pivotValue) {
            list.swap_elems(i, storeI);
            ++storeI;
        }
    int newPivotI = storeI - 1;
    list[startI] = list[newPivotI];
    list[newPivotI] = pivotValue;
    //now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
    return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
    double tmp = list[i];
    list[i] = list[j];
    list[j] = tmp;
}

性能图

谢谢 Gronim，为我指明了正确的方向！

原文

I have a program that needs to repeatedly compute the approximate percentile (order statistic) of a dataset in order to remove outliers before further processing. I'm currently doing so by sorting the array of values and picking the appropriate element; this is doable, but it's a noticable blip on the profiles despite being a fairly minor part of the program.

More info:

The data set contains on the order of up to 100000 floating point numbers, and assumed to be "reasonably" distributed - there are unlikely to be duplicates nor huge spikes in density near particular values; and if for some odd reason the distribution is odd, it's OK for an approximation to be less accurate since the data is probably messed up anyhow and further processing dubious. However, the data isn't necessarily uniformly or normally distributed; it's just very unlikely to be degenerate.
An approximate solution would be fine, but I do need to understand how the approximation introduces error to ensure it's valid.
Since the aim is to remove outliers, I'm computing two percentiles over the same data at all times: e.g. one at 95% and one at 5%.
The app is in C# with bits of heavy lifting in C++; pseudocode or a preexisting library in either would be fine.
An entirely different way of removing outliers would be fine too, as long as it's reasonable.
Update: It seems I'm looking for an approximate selection algorithm.

Although this is all done in a loop, the data is (slightly) different every time, so it's not easy to reuse a datastructure as was done for this question.

Implemented Solution

Using the wikipedia selection algorithm as suggested by Gronim reduced this part of the run-time by about a factor 20.

Since I couldn't find a C# implementation, here's what I came up with. It's faster even for small inputs than Array.Sort; and at 1000 elements it's 25 times faster.

public static double QuickSelect(double[] list, int k) {
    return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
    while (true) {
        // Assume startI <= k < endI
        int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
        int splitI = partition(list, startI, endI, pivotI);
        if (k < splitI)
            endI = splitI;
        else if (k > splitI)
            startI = splitI + 1;
        else //if (k == splitI)
            return list[k];
    }
    //when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
    double pivotValue = list[pivotI];
    list[pivotI] = list[startI];
    list[startI] = pivotValue;

    int storeI = startI + 1;//no need to store @ pivot item, it's good already.
    //Invariant: startI < storeI <= endI
    while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
    //now storeI == endI || list[storeI] > pivotValue
    //so elem @storeI is either irrelevant or too large.
    for (int i = storeI + 1; i < endI; ++i)
        if (list[i] <= pivotValue) {
            list.swap_elems(i, storeI);
            ++storeI;
        }
    int newPivotI = storeI - 1;
    list[startI] = list[newPivotI];
    list[newPivotI] = pivotValue;
    //now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
    return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
    double tmp = list[i];
    list[i] = list[j];
    list[j] = tmp;
}

Performance Graph

Thanks, Gronim, for pointing me in the right direction!

分享到QQ

分享到微博

如果你对这篇内容有疑问，欢迎到本站社区发帖提问参与讨论，获取更多帮助，或者扫码二维码加入 Web 技术交流群。

发布评论

需要登录才能够评论，你可以免费注册一个本站的账号。

-小熊_ 2024-10-01 08:00:25

Henrik 的直方图解决方案将起作用。您还可以使用选择算法在 O(n) 内有效地查找 n 个元素的数组中的 k 个最大或最小元素。要将其用于第 95 个百分位数，请设置 k=0.05n 并找到 k 个最大元素。

参考：

http://en.wikipedia.org/wiki/Selection_algorithm#Selecting_k_smallest_or_largest_elements

回复收藏 0 原文

走野 2024-10-01 08:00:25

根据其创建者 SoftHeap 可用于：

计算精确或近似中位数
和最佳百分位数。这也是
对于近似排序很有用...

回复收藏 0 原文

爱格式化 2024-10-01 08:00:25

我过去常常通过计算标准差来识别异常值。与平均值的距离超过标准差 2（或 3）倍的所有内容都是异常值。 2次=约95%。

由于您正在计算平均值，因此计算标准偏差也非常容易，速度非常快。

您还可以仅使用数据的子集来计算数字。

回复收藏 0 原文

左耳近心 2024-10-01 08:00:25

您可以仅根据数据集的一部分（例如前几千个点）来估计百分位数。

Glivenko–Cantelli 定理确保这将是一个相当不错的估计，如果您可以假设您的数据点是独立的。

回复收藏 0 原文

不打扰别人 2024-10-01 08:00:25

将数据的最小值和最大值之间的间隔划分为（例如）1000 个容器并计算直方图。然后计算部分总和，看看它们在哪里首先超过 5000 或 95000。

回复收藏 0 原文

暮倦 2024-10-01 08:00:25

我能想到几种基本方法。首先是计算范围（通过查找最高值和最低值），将每个元素投影到一个百分位（(x - min) / 范围），并丢弃任何低于 0.05 或高于 0.95 的元素。

第二个是计算平均值和标准差。与平均值（两个方向）的 2 个标准差的跨度将包含 95% 的正态分布样本空间，这意味着您的异常值将位于 <2.5 和 >97.5 百分位内。计算序列的平均值是线性的，标准偏差（每个元素与平均值之差之和的平方根）也是如此。然后，从平均值中减去 2 个西格玛，再将平均值加上 2 个西格玛，就得到了异常值限制。

这两者都将在大致线性时间内进行计算；第一个需要两次通过，第二个需要三次（一旦达到限制，您仍然必须丢弃异常值）。由于这是一个基于列表的操作，我认为您不会发现任何具有对数或恒定复杂度的东西；任何进一步的性能提升都需要优化迭代和计算，或者通过对子样本（例如每三个元素）执行计算来引入误差。

回复收藏 0 原文

瞳孔里扚悲伤 2024-10-01 08:00:25

对您的问题的一个很好的一般答案似乎是RANSAC。
给定一个模型和一些噪声数据，该算法可以有效地恢复模型的参数。
您必须选择一个可以映射您的数据的简单模型。任何光滑的东西都应该没问题。假设几个高斯的混合。 RANSAC 将设置模型的参数并同时估计一组内联器。然后扔掉任何不适合模型的东西。

回复收藏 0 原文

谈场末日恋爱 2024-10-01 08:00:25

即使数据不呈正态分布，您也可以过滤掉 2 或 3 个标准差；至少，这将以一致的方式进行，这应该很重要。

当您删除异常值时，std dev 将发生变化，您可以循环执行此操作，直到 std dev 的变化最小。您是否想要这样做取决于您为什么以这种方式操作数据。一些统计学家对消除异常值持重大保留态度。但有些会删除异常值以证明数据相当正态分布。

回复收藏 0 原文

寂寞美少年 2024-10-01 08:00:25

不是专家，但我的记忆表明：

要准确确定百分位点，您需要排序和计数，
从数据中提取样本并计算百分位值，如果您可以获得良好的样本，则听起来像是一个不错的近似计划，
如果没有，则为Henrik 建议，如果您对桶进行计数并进行计数，则可以避免完全排序

回复收藏 0 原文

横笛休吹塞上声 2024-10-01 08:00:25

一组包含 100k 个元素的数据几乎不需要时间来排序，因此我假设您必须重复执行此操作。如果数据集是同一组，只是稍微更新了一点，那么您最好构建一棵树 (O(N log N))，然后在新点出现时删除和添加新点 (O(K log N)，其中 K 是更改的点数）。否则，前面提到的第 k 个最大元素解决方案将为每个数据集提供 O(N) 。