为什么用余弦计算弧的 x 值，用正弦计算 y 值？

Question

我试图理解这个 raphael.js 演示中的数学：

http://raphaeljs.com/pie.js< /a>

检查扇区方法：

function sector(cx, cy, r, startAngle, endAngle, params) {
    var x1 = cx + r * Math.cos(-startAngle * rad),
        x2 = cx + r * Math.cos(-endAngle * rad),
        y1 = cy + r * Math.sin(-startAngle * rad),
        y2 = cy + r * Math.sin(-endAngle * rad);
    return paper.path(["M", cx, cy, "L", x1, y1, "A", r, r, 0, +(endAngle - startAngle > 180), 0, x2, y2, "z"]).attr(params);
}

这是实际的演示： http://raphaeljs.com/pie.html

我的数学有点生疏，我正在尝试了解扇区函数 - 给定 startAngle 和 endAngle 参数（每个起点和终点值在 0 到 360 之间绘制圆弧），为什么这个函数有效？

Answer 1

只要看看圆中的 sin 和 cos 实际上意味着：

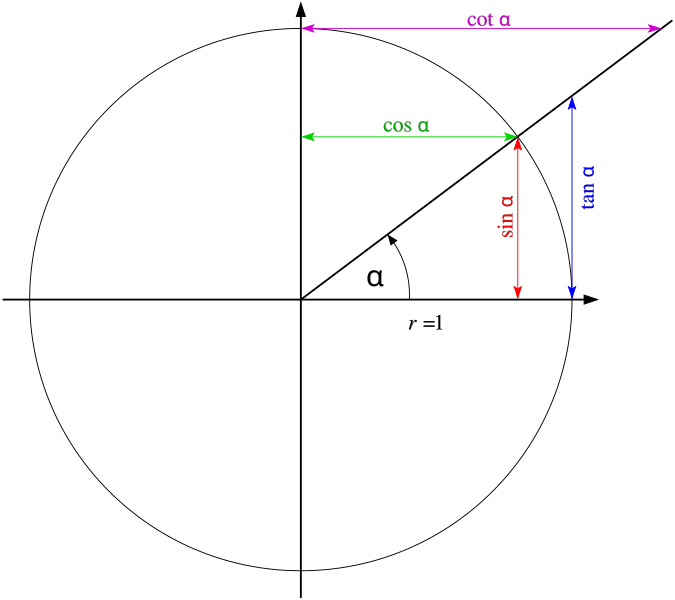
如果您有观点形成角度 alpha 的圆，cos alpha 是点的 x 部分，sin alpha 是 y 部分。

此图解释了为什么角度被否定。

这意味着，您现在可以指定顺时针角度，这是大多数使用模拟时钟的人所喜欢的。

Answer 2

这完全取决于您如何对待 startAngle 和 endAngle。看起来这是将它们视为从水平线向右开始（即 0 度角指向东方）并顺时针方向移动（因此 45 度角指向东南方。

通常在数学中，我们考虑从水平线开始的角度向右，但逆时针增加......但是如果你让一个非数学家画一个角度，他们很可能会从垂直向上（即北）顺时针增加这看起来像是混合了:)有。这里没有真正的“错误”或“正确”答案 - 这都是定义问题。

由于图片很流行，以下是我描述的三个系统，每个系统都假设直线长度为 r：

普通数学：从 x 轴逆时针旋转

_{（来源：arachsys.com）}

要求街上的人画一个角度（从 y 轴顺时针方向）

此代码使用的角度（从 x 轴顺时针方向）

Answer 3

因为以 (cx, cy) 为圆心，以 R 为半径的圆周上的任意点具有以下坐标（它直接从 cos 和 sin 几何定义得出 - 相应的内斜边和斜边的长度之间的比率）：

x = cx + R*cos(a)
y = cy + R*sin(a) for  0 <= a < 2π

因此，对角度 a 进行限制，您可以定义任意的角度 a弧。

Answer 4

如果将 0° 作为水平方向，x 增加，90° 作为垂直方向，y 增加，则：

cos(0) = 1
sin(0) = 0

cos(90) = 0
sin(90) = 1

您可以通过乘以余弦来改变 x 值，并通过乘以正弦来改变 y 值。