弹道曲线问题
好吧,我知道这对于程序员来说是相当离题的,但我仍然需要这个应用程序,所以这里是:
弹道曲线(没有风或任何其他条件)由这两行指定:

所以,有一个问题,你有3个未知值:x,y和时间t,但只有2个方程。 您无法真正仅使用这些值来计算所有 3 个值,我得到:
- 速度 v
- 角度 Alpha
- 原点坐标
因此,您必须决定指定哪一个。
现在你有 2D 坦克游戏,或者类似的东西,你知道你有坦克并使用弹道,你必须以设定的角度和力量击落对手。
我需要知道子弹何时击中地面,它可以在飞行时在空中,也可以预先计算。 我的问题出现了。使用哪种方式?预先计算或检查每一步是否落地。
如果我想预先计算,我需要知道地形的高度,从逻辑上讲,地形的高度必须是恒定的,因为我不知道在哪个 x 坐标。如果我知道 X,那就意味着我的炮塔前面就是墙。因此,当我落地时,获得结果的唯一方法是检查落地的时间间隔。这也很好,因为地形的顶部不是静态的!但这不是太大的开销吗?如果可以变得更简单的话?您遇到过这样的问题/解决方案吗?
预先感谢,顺便说一句,地形可以是平坦的,使用线条或 NURBS,所以我请提供一般解决方案,而不是具体的,因为您在哪个高度拍摄会产生影响。
Ok i know this is quite off-topic for programmers but still I need this for app, so here it is:
Ballistic curve (without wind or any other conditions) is specified by these 2 lines:
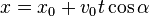
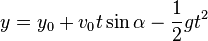
So, there is a problem that you got 3 unknown values: x,y and time t, but only 2 equations.
You can't really compute all 3 with just these values, I got:
- velocity v
- angle Alpha
- origin coordinates
Thus, you have to decide which one to specify.
Now you have 2D tanks game, or anything like that, you know you have tank and using ballistic you have to shoot opponent down with setting angle and power.
I need to know when the bullet hit the ground, it can be on-air as it fly, or precomputed.
There comes up my problem. Which way to use? Pre-compute or check for hitting the ground in each step.
If I would like to pre-compute, I would need to know height of terrain, which, logically would have to be constant as I don't know in which x coord. If I would know the X, it would mean that just in front of my turret is wall. So only way to get to result, when I hit the ground, would be with checking in intervals of time for hitting the ground. This is also good because the terrain doesn't have top be static yay! But isn't that too great overhead which could be made much simpler? Have you encountered with such problem/solution?
Thanks in advance, btw the terrain can be flat, using lines or NURBS so I please for general solution, not specific as in which height you shoot in that will be impact.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(5)
您可以通过求解
t的一个方程并将其代入另一个方程来计算射弹y(x)的路径。你得到然后找到着陆点就是计算该函数与定义地形高度的函数之间的交集。一个交叉路口将是发射点,另一个交叉路口将是着陆点。 (如果您的地形非常陡峭和丘陵,则可能有超过 2 个交叉点,在这种情况下,您将选择第一个
x大于发射点的交叉点。)您可以使用各种 寻根算法来实际计算交集;检查您必须查看的任何数学或游戏物理库的文档,看看它们是否提供了执行此操作的方法。You can compute the path of the projectile
y(x)by solving one equation fortand substituting into the other. You getThen finding the landing point is a matter of computing the intersections between that function and the function that defines the height of the terrain. One intersection will be the launch point and the other will be the landing point. (If your terrain is very steep and hilly, there could be more than 2 intersections, in which case you take the first one with
xgreater than the launch point.) You can use any of various root-finding algorithms to actually compute the intersection; check the documentation of whatever mathematical or game-physical libraries you have to see if they provide a method to do this.David Zaslavsky 很好地回答了您有关求解方程的问题,但如果您的最终目标是简单的弹道模拟,我建议您使用矢量分解。
通过利用向量分解,您可以导出射弹的 x 和 y 分量向量。然后,您可以将加速度应用于每个组件,以考虑重力、风等。然后,您可以将每个时间间隔更新射弹的 (x,y) 位置作为时间的函数。
例如:
那么,如果您可以实现一个简单的 Update 函数,如下所示:
当然,这是一个非常基本示例,但您可以从这里开始构建。
David Zaslavsky did a good job of answering your question about solving for the equation, but if your ultimate goal is simple ballistics simluation, I suggest you instead use vector decomposition.
By utilizing vector decomposition, you can derive the x- and y-compenent vectors of your projectile. You can then apply acceleration to each component to account for gravity, wind, etc. Then you can update the projectile's (x,y) position each interval as a function of time.
For example:
Then if you can impliment a simple Update function as follows:
Of course this is a very basic example, but you can build on it from here.
幸运的是,这是非常简单的运动学。
这些方程是参数化的:对于任何给定的时间
t,它们都会为您提供该时间的 x 和 y 坐标。您所需要做的就是输入起始速度 v 和角度 a。如果您在水平地面上工作,则射弹返回的时间仅为 2sin(a)v/g,即速度的垂直分量除以重力引起的向下加速度。 2 是因为速度下降到 0 需要一定的时间,然后又需要同样的时间才能加速回来。一旦知道时间,您就可以求解 x。
如果你的地形不平坦,你还会有一些额外的乐趣。您可以尝试计算出在相同高度撞击地面的时间,然后纠正额外的垂直距离。这也会改变你的水平距离,这可能会再次影响你的身高……但是进行两到三次调整,误差就会太小,人类无法注意到:)
Fortunately, this is pretty simple kinematics.
Those equations are parametric: For any given time
t, they give you the x and y coordinates for that time. All you need to do is plug in the starting velocity v and angle a.If you're working on level ground, the time for your projectile to come back down is simply 2sin(a)v/g, i.e. the vertical component of your velocity divided by the downward acceleration due to gravity. The 2 is because it takes that amount of time for the speed to drop to 0, then the same time again for it to accelerate back down. Once you know the time you can solve for x.
If your terrain is not flat, you have some additional fun. Something you could try is work out the time for hitting the ground at the same height, and then correct for the extra vertical distance. This will also change your horizontal distance which might again affect your height... but two or three adjustments and the error will be too small for humans to notice :)
我不确定你的做法是否正确。您想要的主要方程是 s = si + vi*dt + .5*adtdt。这是一个简单的一维方程,但它可以清晰地推广到向量。
实际上,si 是您的初始位置,vi 是您的初始速度,a 是重力加速度。
为了实现此目的,请构建一个完美水平枪口速度的矢量并将其投影到发射角度上。那是你的vi。 Si 将是桶的尖端。从那里开始进行矢量求和和缩放。
I'm not sure you're going about this is right way. The main equation you want is s = si + vi*dt + .5*adtdt. This is a simple equation of one dimension, but it generalizes to vectors cleanly.
Effectively, si is your initial position and vi is your initial velocity and a is acceleration due to gravity.
To make this work, build a vector for perfect horizontal muzzle velocity and project it on the launch angle. That's your vi. Si will be the tip of the barrel. From there it's vector summing and scaling.
连续函数对计算机来说效果不佳,因为计算机是隐式离散的:浮点/双精度数字是离散的,计时器是离散的,游戏网格是离散的(即使它使用“双精度”)。
因此,只需按照 Justin Holdsclaw 建议的方式离散化方程即可。每个方向都有速度和加速度矢量(在您的情况下为 X 和 Y;您也可以添加 Z)。在每个刻度处更新所有向量以及对象在空间中的位置。
请注意,结果不会是“准确的”。 “增量”值(网格粗糙度)越小,您就越接近“精确”曲线。要准确了解有多接近 - 如果您有兴趣,请找到一本有关数值分析的书并阅读前几章。出于实际目的,您可以尝试一下。
Continuous functions do not work well for computers, because computers are implicitly discrete: the floating/double numbers are discrete, the timer is discrete, the game grid is discrete (even if it uses 'doubles').
So just discretize the equation the way Justin Holdsclaw suggested. Have velocity and accelerations vectors in each direction (in your case X and Y; you could also add Z). Update all vectors, and the object's position in space, at every tick.
Note that the result won't be 'exact'. The smaller your 'delta' values (grid coarseness), the closer you'll be to the 'exact' curve. To know precisely how close - if you're interested, find a book on numerical analysis and read the first few chapters. For practical purposes you can just experiment a bit.