如何计算两个等维时间序列之间的马氏距离？
我正在对时间序列数据进行一些数据挖掘。我需要计算两个相同维度系列之间的距离或相似度。建议我使用欧几里德距离、Cos 相似度或马哈拉诺比斯距离。前两个没有提供任何有用的信息。我似乎无法理解网络上的各种教程。
那么，
给定两个向量 A(a1, a2, a3,...,an) 和 B(b1, b2, b3,...,bn)，如何找到它们之间的马氏距离？
（我收到了关于在 SO 本身上使用这些距离测量的建议，并且有一个 关于如何计算 Cos 相似度的问题，所以请在关闭此问题之前考虑一下）
I am doing some data-mining on time series data. I need to calculate the distance or similarity between two series of equal dimensions. I was suggested to use Euclidean distance, Cos Similarity or Mahalanobis distance. The first two didn't give any useful information. I cannot seem to understand the various tutorials on the web.
So,
Given two vectors A(a1, a2, a3,...,an) and B(b1, b2, b3,...,bn) how do you find the Mahalanobis distance between them?
(I received advice on using these distance measures on SO itself, and there is a question on how to calculate Cos similarity; so please consider before closing this question)
如果你对这篇内容有疑问，欢迎到本站社区发帖提问 参与讨论，获取更多帮助，或者扫码二维码加入 Web 技术交流群。
绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱，如果其他用户或者作者回复了您的评论，将不能在第一时间通知您！
发布评论
评论（1）
您应该估计协方差矩阵。
维基百科中的相关文章有 this 和 这个。
对于多元向量（p 维变量的 n 个观测值），马氏距离的公式为
其中 S 是协方差矩阵的逆矩阵，可估计为：
其中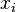
是 ( p 维）随机变量和
请注意，在仅当所有向量的期望值都相同时，向量才有意义。
我一直认为马氏距离仅用于对数据进行分类和检测异常值，例如丢弃实验数据（某种真/假测试）。从未听说过将其用作“类比”距离。
哈！
You should estimate the covariance matrix.
The related articles in Wikipedia are this and this.
For multivariate vectors (n observations of a p-dimensional variable), the formula for the Mahalanobis distance is
Where the S is the inverse of the covariance matrix, which can be estimated as:
where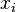
is the i-th observation of the (p-dimensional) random variable and
Be careful that using the Mahalanobis distance between your vectors make sense only if all your vectors expected values are the same.
I always thought that the Mahalanobis distance is only used to classify data and detect outliers, such as discarding experimental data (sort of true/false tests). Never heard of using it as an "analogical" distance.
HTH!