计算有理指数的复数
昨天我创建了这段可以计算 z^n 的代码,其中 z 是复数,n 是任何正整数。
--snip--
float real = 0;
float imag = 0;
// d is the power the number is raised to [(x + yi)^d]
for (int n = 0; n <= d; n++) {
if (n == 0) {
real += pow(a, d);
} else { // binomial theorem
switch (n % 4) {
case 1: // i
imag += bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
case 2: // -1
real -= bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
case 3: // -i
imag -= bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
case 0: // 1
real += bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
}
}
}
--snip--
int factorial(int n) {
int total = 1;
for (int i = n; i > 1; i--) { total *= i; }
return total;
}
// binomial cofactor
float bCo(int n, int k) {
return (factorial(n)/(factorial(k) * factorial(n - k)));
}
我使用二项式定理来展开z^n,并根据虚数的幂知道是否将每一项视为实数或虚数。
我想要做的是能够计算 z^n,其中 n 是任何正实数(分数)。我知道二项式定理可用于非整数的幂,但我不太确定如何处理复数。因为 i^0.1 有实部和虚部,所以我不能将其分类为实部或虚部变量,我什至不知道如何编写可以计算它的程序。
有谁知道可以帮助我完成此任务的算法,或者甚至是处理复数的更好方法,从而使这成为可能?
哦,我用的是java。
谢谢。
Yesterday I created this piece of code that could calculate z^n, where z is a complex number and n is any positive integer.
--snip--
float real = 0;
float imag = 0;
// d is the power the number is raised to [(x + yi)^d]
for (int n = 0; n <= d; n++) {
if (n == 0) {
real += pow(a, d);
} else { // binomial theorem
switch (n % 4) {
case 1: // i
imag += bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
case 2: // -1
real -= bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
case 3: // -i
imag -= bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
case 0: // 1
real += bCo(d, n) * pow(a, d - n) * pow(b, n);
break;
}
}
}
--snip--
int factorial(int n) {
int total = 1;
for (int i = n; i > 1; i--) { total *= i; }
return total;
}
// binomial cofactor
float bCo(int n, int k) {
return (factorial(n)/(factorial(k) * factorial(n - k)));
}
I use the binomial theorem to expand z^n, and know whether to treat each term as a real or imaginary number depending on the power of the imaginary number.
What I want to do is to be able to calculate z^n, where n is any positive real number (fractions). I know the binomial theorem can be used for powers that aren't whole numbers, but I'm not really sure how to handle the complex numbers. Because i^0.1 has a real and imaginary component I can't just sort it into a real or imaginary variable, nor do I even know how to program something that could calculate it.
Does anyone know of an algorithm that can help me accomplish this, or maybe even a better way to handle complex numbers that will make this possible?
Oh, I'm using java.
Thanks.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(4)
首先,它可能有多种解决方案。请参阅维基百科:复数/求幂。
我认为你应该将其分解为极坐标符号并从那里开始。
First of all, it may have multiple solutions. See Wikipedia: Complex number / exponentiation.
I think you should break it down to polar notation and go from there.
考虑一个复数 使得
使得  。
。
因此, 的极坐标形式是 =
的极坐标形式是 =  ,其中:
,其中:
完成此操作后,您可以使用 DeMoivre 定理 来计算 像这样:
像这样:
或更简单地为
有关详细信息,请阅读 复数的极坐标形式。
Consider a complex number such that
such that 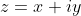 .
.
Thus, the polar form of is =
is =  , where:
, where:
Once you have done so, you can use DeMoivre's Theorem to calculate like so:
like so:
or more simply as
For more information read up on the polar form of a complex number.
我不太擅长数学,所以可能我对你的任务的理解是错误的。但据我所知 - apache commons math 可以帮助你: http://commons .apache.org/math/userguide/complex.html
示例:
I'm not really good at math, so probably I understood your task wrong. But as far as I got it - apache commons math can help you: http://commons.apache.org/math/userguide/complex.html
Example:
当 n 不是整数并且 a 不是正数时,a^n 是错误定义的。
如果 z 是复数,您仍然可以赋予 z^a = exp(a log z) 含义,但您必须弄清楚当 z 不是正数时 log z 的含义。
并且没有唯一的选择。
a^n is ill defined when n is not an integer and a is not a positive number.
If z is a complex number, you can still give a meaning to z^a = exp(a log z) but you have to figure out what log z means when z is not a positive number.
And there is no unique choice.