从 n 维单位单纯形中均匀随机采样
从 n 维单位单纯形中均匀随机采样是一种奇特的方式,表示您想要 n 个随机数,使得
- 它们都是非负的,
- 它们的总和为 1,并且
- n 个非负数的每个可能向量的总和为一个的可能性是相等的。
在 n=2 的情况下,您希望从正象限中的 x+y=1 线段(即 y=1-x)均匀采样。 在 n=3 的情况下,您从平面 x+y+z=1 的三角形部分(位于 R3 的正八分圆内)进行采样:

(图片来自 http://en.wikipedia.org/wiki/Simplex。)
请注意,选择 n 个均匀的随机数然后将它们标准化以使它们总和为 1 是行不通的。你最终会偏向不太极端的数字。
类似地,选择 n-1 个均匀随机数,然后将第 n 个设为 1 减去它们的总和也会引入偏差。
维基百科提供了两种算法来正确执行此操作: http://en.wikipedia.org/wiki/Simplex#随机采样 (尽管第二个目前声称仅在实践中正确,而不是在理论上正确。我希望当我更好地理解这一点时能够清理或澄清它。我最初陷入了“警告:这样那样的论文声明”维基百科页面上的以下内容是错误的”,其他人将其变成了“仅在实践中有效”的警告。)
最后,问题是: 您认为 Mathematica 中单纯形抽样的最佳实现是什么(最好通过经验确认其正确性)?
相关问题
Sampling uniformly at random from an n-dimensional unit simplex is the fancy way to say that you want n random numbers such that
- they are all non-negative,
- they sum to one, and
- every possible vector of n non-negative numbers that sum to one are equally likely.
In the n=2 case you want to sample uniformly from the segment of the line x+y=1 (ie, y=1-x) that is in the positive quadrant.
In the n=3 case you're sampling from the triangle-shaped part of the plane x+y+z=1 that is in the positive octant of R3:
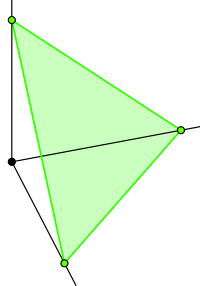
(Image from http://en.wikipedia.org/wiki/Simplex.)
Note that picking n uniform random numbers and then normalizing them so they sum to one does not work. You end up with a bias towards less extreme numbers.
Similarly, picking n-1 uniform random numbers and then taking the nth to be one minus the sum of them also introduces bias.
Wikipedia gives two algorithms to do this correctly: http://en.wikipedia.org/wiki/Simplex#Random_sampling
(Though the second one currently claims to only be correct in practice, not in theory. I'm hoping to clean that up or clarify it when I understand this better. I initially stuck in a "WARNING: such-and-such paper claims the following is wrong" on that Wikipedia page and someone else turned it into the "works only in practice" caveat.)
Finally, the question:
What do you consider the best implementation of simplex sampling in Mathematica (preferably with empirical confirmation that it's correct)?
Related questions
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(6)
此代码可以工作:
基本上,您只需在间隔
[0,1]上选择n - 1个位置即可将其分割,然后使用 < 获取每个部分的大小代码>差异。快速运行
Timing表明它比 Janus 的第一个答案要快一点。This code can work:
Basically you just choose
n - 1places on the interval[0,1]to split it up then take the size of each of the pieces usingDifferences.A quick run of
Timingon this shows that it's a little faster than Janus's first answer.经过一番挖掘后,我发现 此页面 它提供了一个很好的实现狄利克雷分布。从这里看来,遵循维基百科的方法 1 似乎非常简单。这似乎是最好的方法。
作为测试:
100 个样本的图:
替代文本 http://www. public.iastate.edu/~zdavkeos/simplex-sample.png
After a little digging around, I found this page which gives a nice implementation of the Dirichlet Distribution. From there it seems like it would be pretty simple to follow Wikipedia's method 1. This seems like the best way to do it.
As a test:
A plot of 100 samples:
alt text http://www.public.iastate.edu/~zdavkeos/simplex-sample.png
我支持 zdav:狄利克雷分布似乎是最简单的方法,zdav 所指的狄利克雷分布采样算法也出现在 狄利克雷分布。
在实现方面,首先执行完整的狄利克雷分布会产生一些开销,因为您真正需要的是
n个随机Gamma[1,1]样本。比较如下简单实现
完整 Dirichlet 实现
时序
因此,完整 Dirichlet 速度慢了 3 倍。如果您一次需要 m>1 个样本点,您可能可以通过执行
(#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}].I'm with zdav: the Dirichlet distribution seems to be the easiest way ahead, and the algorithm for sampling the Dirichlet distribution which zdav refers to is also presented on the Wikipedia page on the Dirichlet distribution.
Implementationwise, it is a bit of an overhead to do the full Dirichlet distribution first, as all you really need is
nrandomGamma[1,1]samples. Compare belowSimple implementation
Full Dirichlet implementation
Timing
So the full Dirichlet is a factor of 3 slower. If you need m>1 samplepoints at a time, you could probably win further by doing
(#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}].这是来自 Wikipedia 的第二种算法的简洁实现:
改编自此处:http://www.mofeel.net/1164-comp-soft -sys-math-mathematica/14968.aspx
(最初它使用 Union 而不是 Sort@Join ——后者稍微快一些。)
(请参阅评论以获取一些证明这是正确的证据!)
Here's a nice concise implementation of the second algorithm from Wikipedia:
That's adapted from here: http://www.mofeel.net/1164-comp-soft-sys-math-mathematica/14968.aspx
(Originally it had Union instead of Sort@Join -- the latter is slightly faster.)
(See comments for some evidence that this is correct!)
我创建了一种在单纯形上均匀随机生成的算法。您可以在以下链接中找到论文的详细信息:
http://www.tandfonline.com/doi/abs/10.1080 /03610918.2010.551012#.U5q7inJdVNY
简而言之,您可以使用以下递归公式来查找n维单纯形上的随机点:
x1=1 -R11/n-1
xk=(1-Σi=1kxi)(1-Rk1/nk), k=2, .. ., n-1
xn=1-Σi=1n-1xi
其中 R_i 是 0 到 1 之间的随机数。
现在我正在尝试制定一种算法来从受约束生成随机均匀样本单纯形。即单纯形和凸体之间的交集。
I have created an algorithm for uniform random generation over a simplex. You can find the details in the paper in the following link:
http://www.tandfonline.com/doi/abs/10.1080/03610918.2010.551012#.U5q7inJdVNY
Briefly speaking, you can use following recursion formulas to find the random points over the n-dimensional simplex:
x1=1-R11/n-1
xk=(1-Σi=1kxi)(1-Rk1/n-k), k=2, ..., n-1
xn=1-Σi=1n-1xi
Where R_i's are random number between 0 and 1.
Now I am trying to make an algorithm to generate random uniform samples from constrained simplex.that is intersection between a simplex and a convex body.
老问题,我迟到了,但如果有效实施,这种方法比接受的答案要快得多。
在 Mathematica 代码中:
#/Total[#,{2}]&@Log@RandomReal[{0,1},{n,d}]
用简单的英语来说,您生成 n 行 * d 列均匀分布在 0 和 1 之间的随机数。然后记录一切。然后标准化每一行,将行中的每个元素除以行总数。现在您有 n 个样本均匀分布在 (d-1) 维单纯形上。
如果在这里找到此方法:https://mathematica。 stackexchange.com/questions/33652/uniformly-distributed-n-Dimensions-probability-vectors-over-a-simplex
我承认,我不确定它为什么有效,但它通过了我的每一个统计测试可以想到。如果有人能证明这种方法为何有效,我很乐意看到它!
Old question, and I'm late to the party, but this method is much faster than the accepted answer if implemented efficiently.
In Mathematica code:
#/Total[#,{2}]&@Log@RandomReal[{0,1},{n,d}]
In plain English, you generate n rows * d columns of randoms uniformly distributed between 0 and 1. Then take the Log of everything. Then normalize each row, dividing each element in the row by the row total. Now you have n samples uniformly distributed over the (d-1) dimensional simplex.
If found this method here: https://mathematica.stackexchange.com/questions/33652/uniformly-distributed-n-dimensional-probability-vectors-over-a-simplex
I'll admit, I'm not sure why it works, but it passes every statistical test I can think of. If anyone has a proof of why this method works, I'd love to see it!