有条件地为 R 中置信带之外的数据点着色

Question

我需要对下图中置信带之外的数据点与带内的数据点进行不同的着色。我是否应该在数据集中添加一个单独的列来记录数据点是否在置信区间内？您能举个例子吗？

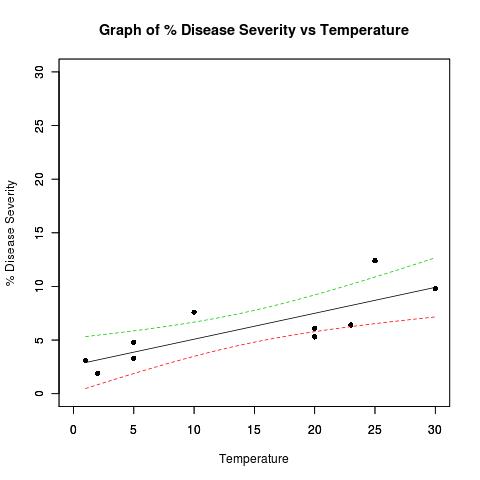
示例数据集：

## Dataset from http://www.apsnet.org/education/advancedplantpath/topics/RModules/doc1/04_Linear_regression.html

## Disease severity as a function of temperature

# Response variable, disease severity
diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)

# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)

## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))

## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)

# Take a look at the data
plot(
  diseasesev~temperature,
  data=severity,
  xlab="Temperature",
  ylab="% Disease Severity",
  pch=16,
  pty="s",
  xlim=c(0,30),
  ylim=c(0,30)
)
title(main="Graph of % Disease Severity vs Temperature")
par(new=TRUE) # don't start a new plot

## Get datapoints predicted by best fit line and confidence bands
## at every 0.01 interval
xRange=data.frame(temperature=seq(min(temperature),max(temperature),0.01))
pred4plot <- predict(
                        lm(diseasesev~temperature),
                        xRange,
                        level=0.95,
                        interval="confidence"
                    )

## Plot lines derrived from best fit line and confidence band datapoints
matplot(
  xRange,
  pred4plot,
  lty=c(1,2,2),   #vector of line types and widths
  type="l",       #type of plot for each column of y
  xlim=c(0,30),
  ylim=c(0,30),
  xlab="",
  ylab=""
)

Answer 1

好吧，我认为使用 ggplot2 这会很容易，但现在我意识到我不知道如何计算 stat_smooth/geom_smooth 的置信限。

考虑以下情况：

library(ggplot2)
pred <- as.data.frame(predict(severity.lm,level=0.95,interval="confidence"))
dat <- data.frame(diseasesev,temperature, 
    in_interval = diseasesev <=pred$upr & diseasesev >=pred$lwr ,pred)
ggplot(dat,aes(y=diseasesev,x=temperature)) +
stat_smooth(method='lm')  + geom_point(aes(colour=in_interval)) +
    geom_line(aes(y=lwr),colour=I('red')) + geom_line(aes(y=upr),colour=I('red'))

这会产生：
替代文本 http://ifellows.ucsd.edu/pmwiki/uploads/Main/strangeplot.jpg

我不明白为什么 stat_smooth 计算的置信带与直接从预测计算的带（即红线）不一致。有人能解释一下吗？

编辑：

弄清楚了。 ggplot2 使用 1.96 * 标准误差来绘制所有平滑方法的间隔。

pred <- as.data.frame(predict(severity.lm,se.fit=TRUE,
        level=0.95,interval="confidence"))
dat <- data.frame(diseasesev,temperature, 
    in_interval = diseasesev <=pred$fit.upr & diseasesev >=pred$fit.lwr ,pred)
ggplot(dat,aes(y=diseasesev,x=temperature)) +
    stat_smooth(method='lm')  + 
    geom_point(aes(colour=in_interval)) +
    geom_line(aes(y=fit.lwr),colour=I('red')) + 
    geom_line(aes(y=fit.upr),colour=I('red')) +
    geom_line(aes(y=fit.fit-1.96*se.fit),colour=I('green')) + 
    geom_line(aes(y=fit.fit+1.96*se.fit),colour=I('green'))

Answer 2

最简单的方法可能是计算一个由 TRUE/FALSE 值组成的向量，该向量指示数据点是否位于置信区间内。我将稍微重新调整您的示例，以便在执行绘图命令之前完成所有计算 - 这在程序逻辑中提供了干净的分离，如果您要将其中一些打包到函数中，则可以利用该分离。

第一部分几乎相同，只是我用 severity.lm 变量替换了 predict() 中对 lm() 的额外调用- 当我们已经存储线性模型时，无需使用额外的计算资源来重新计算线性模型：

## Dataset from 
#  apsnet.org/education/advancedplantpath/topics/
#    RModules/doc1/04_Linear_regression.html

## Disease severity as a function of temperature

# Response variable, disease severity
diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)

# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)

## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))

## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)

## Get datapoints predicted by best fit line and confidence bands
## at every 0.01 interval
xRange=data.frame(temperature=seq(min(temperature),max(temperature),0.01))
pred4plot <- predict(
  severity.lm,
  xRange,
  level=0.95,
  interval="confidence"
)

现在，我们将计算原始数据点的置信区间并运行测试以查看这些点是否在区间内：

modelConfInt <- predict(
  severity.lm,
  level = 0.95,
  interval = "confidence"
)

insideInterval <- modelConfInt[,'lwr'] < severity[['diseasesev']] &
  severity[['diseasesev']] < modelConfInt[,'upr']

然后我们将首先使用高级绘图函数 plot() 进行绘图，就像您在示例中使用的那样，但我们只会绘制区间内的点。然后，我们将使用低级函数 points() ，它将用不同的颜色绘制区间外的所有点。最后，matplot() 将用于填充您使用的置信区间。然而，我更喜欢将参数 add=TRUE 传递给高级函数，以使它们像低级函数一样运行，而不是调用 par(new=TRUE)。

使用 par(new=TRUE) 就像在绘图函数中玩弄肮脏的把戏 - 这可能会产生不可预见的后果。许多函数都提供 add 参数，使它们向绘图添加信息而不是重新绘制它 - 我建议尽可能利用此参数并依靠 par() 将操纵作为最后的手段。

# Take a look at the data- those points inside the interval
plot(
  diseasesev~temperature,
  data=severity[ insideInterval,],
  xlab="Temperature",
  ylab="% Disease Severity",
  pch=16,
  pty="s",
  xlim=c(0,30),
  ylim=c(0,30)
)
title(main="Graph of % Disease Severity vs Temperature")

# Add points outside the interval, color differently
points(
  diseasesev~temperature,
  pch = 16,
  col = 'red',
  data = severity[ !insideInterval,]
)

# Add regression line and confidence intervals
matplot(
  xRange,
  pred4plot,
  lty=c(1,2,2),   #vector of line types and widths
  type="l",       #type of plot for each column of y
  add = TRUE
)

Answer 3

我喜欢这个想法并尝试为此创建一个函数。当然，它还远未达到完美。欢迎您提出意见，

diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)
# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)

## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))

## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)

# Function to plot the linear regression and overlay the confidence intervals   
ci.lines<-function(model,conf= .95 ,interval = "confidence"){
  x <- model[[12]][[2]]
  y <- model[[12]][[1]]
  xm<-mean(x)
  n<-length(x)
  ssx<- sum((x - mean(x))^2)
  s.t<- qt(1-(1-conf)/2,(n-2))
  xv<-seq(min(x),max(x),(max(x) - min(x))/100)
  yv<- coef(model)[1]+coef(model)[2]*xv

  se <- switch(interval,
        confidence = summary(model)[[6]] * sqrt(1/n+(xv-xm)^2/ssx),
        prediction = summary(model)[[6]] * sqrt(1+1/n+(xv-xm)^2/ssx)
              )
  # summary(model)[[6]] = 'sigma'

  ci<-s.t*se
  uyv<-yv+ci
  lyv<-yv-ci
  limits1 <- min(c(x,y))
  limits2 <- max(c(x,y))

  predictions <- predict(model, level = conf, interval = interval)

  insideCI <- predictions[,'lwr'] < y & y < predictions[,'upr']

  x_name <- rownames(attr(model[[11]],"factors"))[2]
  y_name <- rownames(attr(model[[11]],"factors"))[1]

  plot(x[insideCI],y[insideCI],
  pch=16,pty="s",xlim=c(limits1,limits2),ylim=c(limits1,limits2),
  xlab=x_name,
  ylab=y_name,
  main=paste("Graph of ", y_name, " vs ", x_name,sep=""))

  abline(model)

  points(x[!insideCI],y[!insideCI], pch = 16, col = 'red')

  lines(xv,uyv,lty=2,col=3)
  lines(xv,lyv,lty=2,col=3)
}

请像这样使用它：

ci.lines(severity.lm, conf= .95 , interval = "confidence")
ci.lines(severity.lm, conf= .85 , interval = "prediction")