阴阳拼图是如何运作的?
我试图掌握Scheme中call/cc的语义,关于延续的维基百科页面以阴阳谜题为例:
(let* ((yin
((lambda (cc) (display #\@) cc) (call-with-current-continuation (lambda (c) c))))
(yang
((lambda (cc) (display #\*) cc) (call-with-current-continuation (lambda (c) c)))) )
(yin yang))
它应该输出@*@**@***@*** *@...,
但我不明白为什么;我希望它输出 @*@*********...
有人可以详细解释为什么阴阳谜题会这样工作吗?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(8)
正如另一个答案所说,我们首先用
get-cc简化(call-with-current-continuation (lambda (c) c))。现在,这两个 lambda 只是一个具有副作用的相同函数。我们将这些函数称为
f(对于display #\@)和g(对于display #\*)。接下来我们需要制定评估顺序。为了清楚起见,我将引入一个“步骤表达式”,它使每个评估步骤都明确。首先我们问:上面的功能需要什么?
它需要
f和g的定义。在步骤表达式中,我们写第一步是计算
yin,但这需要评估(f get-cc),而后面需要get-cc。粗略地说,
get-cc为您提供一个表示“当前延续”的值。假设这是s1,因为这是下一步。所以我们写注意参数是无范围的,这意味着
s0和s1中的f和g不是必要的相同,并且它们只能在当前步骤中使用。这使得上下文信息变得明确。现在,cc的值是多少?由于它是“当前延续”,因此它与s1相同,其中f和g绑定到相同的值。一旦我们有了
cc,我们就可以评估f get-cc。另外,由于以下代码中未使用f,因此我们不必传递该值。接下来是
yang的类似情况。但现在我们还有一个价值可以传递:yin。最后,最后一步是将
阳应用到阴。这样就完成了步骤表达式的构造。将其翻译回Scheme很简单:
详细的求值顺序(这里
s2主体内的lambda简单地表示为部分求值s3 yin而不是(lambda (cc) (s3 yin cc))):(请记住,在计算
s2或s4时,将首先计算参数As another answer said, we first simplify
(call-with-current-continuation (lambda (c) c))withget-cc.Now, the two lambda are just a identical function associated with side-effects. Let's call those functions
f(fordisplay #\@) andg(fordisplay #\*).Next we need to work out the evaluation order. To be clear, I will introduce a "step expression" which makes every evaluation step explicit. First let's ask: what is the above function requires?
It requires definitions of
fandg. In step expression, we writeThe first step is to calculate
yin, but that require evaluate of(f get-cc), and the later requireget-cc.Roughly speaking,
get-ccgives you a value that represents the "current continuation". Let's say this iss1since this is the next step. So we writeNote that the parameters are scopeless, which means the
fandgins0ands1are not necessary the same and they are only to be used within the current step. This makes the context information explicit. Now, what is the value forcc? Since it is "current continuation", it is kind of the sames1withfandgbound to the same value.Once we have
cc, we can evaluatef get-cc. Also, sincefis not used in the following code, we don't have to pass on this value.The next is the similar for
yang. But now we have one more value to pass on:yin.Finally, the last step is to apply
yangtoyin.This finished the construct of step expression. Translate it back to Scheme is simple:
The detailed evaluation order (here the lambda inside the body of
s2was simply expressed as partial evaluations3 yinrather than(lambda (cc) (s3 yin cc))):(Remember, when evaluating
s2ors4, the parameter is going to be evaluated first这是混淆大师 David Madore 的一个古老谜题,他
创建了 Unlambda。 comp.lang.scheme 中已经讨论过几个谜题
次。
泰勒坎贝尔提出了一个很好的解决方案:
https://groups.google.com/d/msg/comp .lang.scheme/pUedvrKYY5w/uIjTc_T1LOEJ
David Madore 的原始帖子 (1999):
https://groups.google.com/d/msg/comp .lang.scheme/Fysq_Wplxsw/awxEZ_uxW20J
This an old puzzle from the master of obfuscation David Madore, who
created Unlambda. The puzzle has been discussed comp.lang.scheme several
times.
A nice solution from Taylor Campbell:
https://groups.google.com/d/msg/comp.lang.scheme/pUedvrKYY5w/uIjTc_T1LOEJ
The original post from David Madore (1999):
https://groups.google.com/d/msg/comp.lang.scheme/Fysq_Wplxsw/awxEZ_uxW20J
我心里还不知道,但我可以用 Unlambda 变体中的铅笔和纸来推断它。
阴阳谜题的 Unlambda 变体是:
其运行结果是:(
在维基百科页面中查看它 call/cc: Examples。)
我已经推断出这是如何产生的,我正在展示 LaTeX 中的树重写和连续重新插入:
I do not know yet with my heart, but I can deduce it with pencil and paper in the Unlambda variant.
The Unlambda variant of the ying-yang puzzle is:
and its run result is:
(see it among the Wikipedia page call/cc: examples.)
I have deduced how this is coming out, I am showing the tree rewritings and the continution repluggings in LaTeX:
这是类似于 JavaScript 的伪代码翻译:
Here's a translation to pseudocode similar to JavaScript:
理解Scheme
我认为理解这个难题的至少一半问题是Scheme 语法,大多数人都不熟悉它。
首先,我个人发现
call/cc x比等效的替代方案x get/cc更难理解。它仍然调用 x,将当前的延续传递给它,但不知何故更适合在我的大脑电路中表示。考虑到这一点,构造
(call-with-current-continuation (lambda (c) c))就变成了简单的get-cc。现在我们要做的是:下一步是内部 lambda 的主体。
(display #\@) cc,在更熟悉的语法中(对我来说,无论如何)意味着print @;返回抄送;。在我们这样做的同时,我们还将lambda (cc) body重写为function (arg) { body },删除一堆括号,并将函数调用更改为类似 C 的语法,了解一下:现在开始变得更有意义了。现在只需将其完全重写为类似 C 的语法(或类似 JavaScript,如果您愿意)即可:
最难的部分现在已经结束,我们已经从Scheme 中解码了它!只是在开玩笑;只是很难,因为我以前没有使用Scheme 的经验。那么,让我们来看看它实际上是如何工作的。
延续入门
观察阴阳的奇怪表述的核心:它定义了一个函数然后立即调用它。它看起来就像
(function(a,b) { return a+b; })(2, 3),可以简化为5。但是简化 yin/yang 内部的调用将是一个错误,因为我们没有向它传递一个普通值。我们向函数传递一个延续。乍一看,延续是一头奇怪的野兽。考虑一个更简单的程序:
最初
x设置为当前的延续对象(请耐心等待),并且print x被执行,打印类似 的内容; 但延续就像一个函数;它可以用一个参数来调用。它的作用是:获取参数,然后跳转到创建延续的位置,恢复所有上下文,并使其
get-cc返回该参数。在我们的示例中,参数是
5,因此我们本质上直接跳回到var x = get-cc语句的中间,只是这次get- cc返回5。因此,x变为5,下一条语句继续打印 5。之后,我们尝试调用5(5),这是一个类型错误,程序崩溃。请注意,调用延续是跳转,而不是调用。它永远不会返回到调用延续的地方。这很重要。
程序如何工作
如果您遵循了这一点,那么就不要抱太大希望:这部分确实是最难的。这是我们的程序,删除了变量声明,因为无论如何这都是伪代码:
第一次到达第 1 行和第 2 行,它们现在很简单:获取延续,调用函数(arg),打印
@,返回,将该延续存储在yin中。与yang相同。我们现在已经打印了@*。接下来,我们在
yin中调用延续,并将其传递给yang。这使我们跳转到第 1 行,就在 get-cc 内部,并使其返回yang。现在,yang的值被传递到函数中,该函数打印@,然后返回yang的值。现在,yin被分配了yang所具有的延续。接下来我们继续执行第 2 行:获取 c/c,打印*,将 c/c 存储在yang中。我们现在有@*@*。最后,我们转到第 3 行。请记住,
yin现在具有首次执行第 2 行时的延续。因此,我们跳转到第 2 行,打印第二个*并更新yang。我们现在有@*@**。最后,再次调用yin延续,它将跳转到第 1 行,打印@。等等。坦率地说,此时我的大脑抛出了 OutOfMemory 异常,我忘记了一切。但至少我们到达了@*@**!显然,这很难理解,甚至更难解释。执行此操作的完美方法是在可以代表延续的调试器中单步执行它,但可惜的是,我不知道有任何延续。我希望你喜欢这个;我当然有。
Understanding Scheme
I think at least half of the problem with understanding this puzzle is the Scheme syntax, which most are not familiar with.
First of all, I personally find the
call/cc xto be harder to comprehend than the equivalent alternative,x get/cc. It still calls x, passing it the current continuation, but somehow is more amenable to being represented in my brain circuitry.With that in mind, the construct
(call-with-current-continuation (lambda (c) c))becomes simplyget-cc. We’re now down to this:The next step is the body of the inner lambda.
(display #\@) cc, in the more familiar syntax (to me, anyway) meansprint @; return cc;. While we’re at it, let’s also rewritelambda (cc) bodyasfunction (arg) { body }, remove a bunch of parentheses, and change function calls to the C-like syntax, to get this:It’s starting to make more sense now. It’s now a small step to rewrite this completely into C-like syntax (or JavaScript-like, if you prefer), to get this:
The hardest part is now over, we’ve decoded this from Scheme! Just kidding; it was only hard because I had no previous experience with Scheme. So, let’s get to figuring out how this actually works.
A primer on continuations
Observe the strangely formulated core of yin and yang: it defines a function and then immediately calls it. It looks just like
(function(a,b) { return a+b; })(2, 3), which can be simplified to5. But simplifying the calls inside yin/yang would be a mistake, because we’re not passing it an ordinary value. We’re passing the function a continuation.A continuation is a strange beast at first sight. Consider the much simpler program:
Initially
xis set to the current continuation object (bear with me), andprint xgets executed, printing something like<ContinuationObject>. So far so good.But a continuation is like a function; it can be called with one argument. What it does is: take the argument, and then jump to wherever that continuation was created, restoring all context, and making it so that
get-ccreturns this argument.In our example, the argument is
5, so we essentially jump right back into the middle of thatvar x = get-ccstatement, only this timeget-ccreturns5. Soxbecomes5, and the next statement goes on to print 5. After that we try to call5(5), which is a type error, and the program crashes.Observe that calling the continuation is a jump, not a call. It never returns back to where the continuation was called. That’s important.
How the program works
If you followed that, then don’t get your hopes up: this part is really the hardest. Here’s our program again, dropping the variable declarations because this is pseudo-code anyway:
The first time line 1 and 2 are hit, they are simple now: get the continuation, call the function(arg), print
@, return, store that continuation inyin. Same withyang. We’ve now printed@*.Next, we call the continuation in
yin, passing ityang. This makes us jump to line 1, right inside that get-cc, and make it returnyanginstead. The value ofyangis now passed into the function, which prints@, and then returns the value ofyang. Nowyinis assigned that continuation thatyanghas. Next we just proceed to line 2: get c/c, print*, store the c/c inyang. We now have@*@*. And lastly, we go to line 3.Remember that
yinnow has the continuation from when line 2 was first executed. So we jump to line 2, printing a second*and updatingyang. We now have@*@**. Lastly, call theyincontinuation again, which will jump to line 1, printing a@. And so on. Frankly, at this point my brain throws an OutOfMemory exception and I lose track of everything. But at least we got to@*@**!This is hard to follow and even harder to explain, obviously. The perfect way to do this would be to step through it in a debugger which can represent continuations, but alas, I don’t know of any. I hope you have enjoyed this; I certainly have.
我不认为我完全理解这一点,但我只能想到一个(极端手波)解释:
yin和yang首先绑定在let*中。(yin yang)被应用,并且在第一次呼叫/抄送完成后立即返回到顶部。yin被重新绑定到第二个 call/cc 的值。(yin yang),但这次它在原始yang的环境中执行,其中yin绑定到第一个 call/cc,因此控制返回到打印另一个 @。yang参数包含在第二次传递时重新捕获的延续,正如我们已经看到的,这将导致打印**。因此,在第三遍中,将打印@*,然后调用此双星打印延续,因此最终得到 3 颗星,然后重新捕获此三星延续, ...I don't think I understand this one fully, but I can only think of one (extremely hand-wavy) explanation for this:
yinandyangare first bound in thelet*.(yin yang)is applied, and it goes back to the top, right after the first call/cc is finished.yinis re-bound to the value of the second call/cc.(yin yang)is applied again, but this time it's executing in the originalyang's environment, whereyinis bound to the first call/cc, so control goes back to printing another @. Theyangargument contains the continuation that was re-captured on the second pass through, which as we've already seen, will result in printing**. So on this third pass,@*will be printed, then this double-star-printing continuation gets invoked, so it ends up with 3 stars, and then this triple-star continuation is re-captured, ...阴阳谜题是用Scheme编写的。我假设您知道Scheme 的基本语法。
但我假设您不知道
let*或call-with-current-continuation,我将解释这两个关键字。解释
let*如果您已经知道这一点,可以跳到
解释 call-with-current-continuationlet*,它看起来像let,作用类似于let,但会评估其定义的变量((yin ...)和(yang ...)< /code>) 一一热切地。这意味着,它将首先评估yin,然后评估yang。您可以在这里阅读更多内容:
在Scheme中使用Let
解释
call-with-current-continuation如果你已经知道了,你可以跳到
阴阳谜题。解释
call-with-current-continuation有点困难。所以我用一个比喻来解释一下。想象一个知道咒语的巫师,该咒语是
call-with-current-continuation。一旦施展咒语,他就会创造出一个新的宇宙,并将自己送入其中。但在新宇宙中他什么也做不了,只能等待有人叫他的名字。一旦被召唤,巫师就会回到原来的宇宙,带着那个可怜的家伙——“某人”——继续他的巫师生活。如果没有被召唤,当新宇宙结束时,巫师也会回到原来的宇宙。好吧,让我们更技术一些。
call-with-current-continuation是一个接受函数作为参数的函数。一旦你用函数F调用call-with-current-continuation,它就会打包当前的运行环境,称为current-continuation,作为参数C,发送给函数F,并执行F。所以整个程序就变成了(FC)。或者更多的 JavaScript:F(C);。C的行为就像一个函数。如果F中没有调用C,那么它是一个普通程序,当F返回时,call-with-current-continuation的值是F的返回值。但如果使用参数V调用C,则会再次改变整个程序。当call-with-current-continuation被调用时,程序会变回状态。但现在call-with-current-continuation产生一个值,即V。该计划仍在继续。让我们举个例子。
当然,第一个
display输出3。但第二个
display输出2。为什么?让我们深入探讨一下。
当计算
(display (call-with-current-continuation f))时,它会首先计算(call-with-current-continuation f)。我们知道它会将整个程序更改为考虑到
f的定义,它有一个(return 2)。我们必须评估(C 2)。这就是调用continuation的时候。因此它将整个程序更改回但现在,
call-with-current-continuation的值为2。所以程序就变成了:阴阳谜题
让我们看一下这个谜题。
让我们让它更具可读性。
让我们在大脑中运行该程序。
第 0 轮
let*让我们首先评估yin。yin是所以我们首先评估id。但
(call-with-current-continuation id)。它打包了当前环境,我们将其称为C_0以与时间线中的其他延续区分开来,并进入一个全新的宇宙:id仅返回C_0。我们应该记住
C_0是什么。C_0是这样的程序:###是一个占位符,将来将由C_0取回的值填充。但
id仅返回C_0。它不会调用C_0。如果它调用,我们将进入C_0的宇宙。但事实并非如此,所以我们继续评估yin。f是一个类似于id的函数,但它有一个副作用——输出@。因此程序输出
@并令yin为C_0。现在程序变成在
yin计算之后,我们开始计算yang。yang是call-with-current-continuation,这里创建另一个延续,命名为C_1。C_1是:###是占位符。请注意,在此延续中,yin的值已确定(这就是let*所做的)。我们确定这里yin的值为C_0。由于
(id C_1)为C_1,因此yang的值为g有一个副作用 - 输出<代码>*。程序也是如此。yang的值现在为C_1。到目前为止,我们已经显示了
@*所以现在它变成:
由于
yin和yang都已解决,我们应该评估(yin阳)。这真是天哪!
但最终,
C_0被调用。所以我们飞进了C_0宇宙并忘记了所有这些狗屎。我们永远不会再回到这个宇宙了。第 1 轮
C_0与C_1一起进行。现在程序就变成了(如果你忘了C_0代表什么,回头看看):啊,我们发现
yin的值还没有确定。所以我们对其进行评估。在计算yin的过程中,我们输出一个@作为f的副作用。我们现在知道yin是C_1。我们开始评估
yang,我们再次遇到call-with-current-continuation。我们是练过的。我们创建一个延续C_2,它代表:我们在
g执行时显示一个*。我们来到这里所以我们得到:
你知道我们要去哪里。我们要去
C_1的宇宙。我们从记忆中回忆它(或从网页复制并粘贴)。现在:我们知道在
C_1的宇宙中,yin的值已经确定。所以我们开始评估yang。当我们练习时,我会直接告诉你,它显示*并变成:现在我们已经打印了
@*@**,我们将要C_0使用C_2获取宇宙。第 2 轮
当我们练习时,我会告诉你,我们显示“@”,
yin是C_2,并且我们创建一个新的延续C_3,它代表:我们显示
*,yang是C_3,就变成了And we can continue。但我就到这里为止,我已经向你展示了阴阳谜题的前几个输出是什么。
为什么
*的数量增加了?现在你的脑子里充满了细节。我给大家做一个总结。
我将使用类似 Haskell 的语法来简化。
cc是call-with-current-continuation的缩写。当
#C_i#被#括起来时,表示在此创建延续。;表示输出如果你仔细观察,你会发现
C_0是唯一以 < 开始的宇宙代码>f。其他的则由g启动。C_0 C_n始终会产生新的延续C_max。这是因为C_0是g cc id未被执行的第一个Universe。C_0 C_n还显示@。C_n C_mn 不为 0 时将显示*。C_0 C_n,我将证明C_0 C_n被越来越多的其他表达式分隔开,从而导致@*@ **@***...一点数学
假设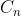 (n != 0 ) 是所有延续中最大的编号,然后调用
(n != 0 ) 是所有延续中最大的编号,然后调用
C_0 C_n。假设:当
C_0 C_n被调用时,C_n是当前最大编号的延续。现在 由
由
C_0 C_n创建,如下所示:因此我们得出结论:
定理I. 如果调用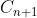 ,其中
,其中
C_0 C_n,它将产生一个延续yin为C_n。然后下一步是
C_n C_{n+1}。yin之所以是C_{n-1},是因为C_n在创建时遵循定理I。然后调用
C_{n-1} C_{n+1},我们知道当C_{n-1}创建时,它也遵循定理一。所以我们有C_{n-2} C_{n+1}。C_{n+1}是不变的。所以我们有第二个定理:定理 II。如果
C_n C_m其中nm 和 n > 0被调用,它将变成C_{n-1} C_m。并且我们已经手动检查了
C_0C_1C_2C_3。他们遵守假设和所有定理。我们知道第一个@和*是如何创建的。所以我们可以写出下面的模式。
它不是那么严格,但我想写:
QED
YinYang puzzle is written in Scheme. I assume you know the basic syntax of Scheme.
But I assume you don't know
let*orcall-with-current-continuation, I will explain these two keywords.Explain
let*If you already know that, you can skip to
Explain call-with-current-continuationlet*, which looks likelet, acts likelet, but will evaluate its defined variables(the(yin ...)and(yang ...)) one by one and eagerly. That means, it will first evaluateyin, and thanyang.You can read more in here:
Using Let in Scheme
Explain
call-with-current-continuationIf you already know that, you can skip to
Yin-Yang puzzle.It's a little bit hard to explain
call-with-current-continuation. So I will use a metaphor to explain it.Image a wizard who knew a spell, which was
call-with-current-continuation. Once he cast the spell, he would create a new universe, and send him-self to it. But he could do nothing in the new universe but waiting for someone calling his name. Once been called, the wizard would return to the original universe, having the poor guy -- 'someone' -- in hand, and go on his wizard life. If not been called, when the new universe ended, the wizard also returned to the original universe.Ok, let's be more technical.
call-with-current-continuationis a function which accept a function as parameter. Once you callcall-with-current-continuationwith a functionF, it will pack the current running environment, which is calledcurrent-continuation, as a parameterC, and send it to functionF, and executeF. So the whole program becomes(F C). Or being more JavaScript:F(C);.Cacts like a function. IfCis not called inF, then it is an ordinary program, whenFreturns,call-with-current-continuationhas a value asF's return value. But ifCis called with a parameterV, it will change the whole program again. The program changes back to a state whencall-with-current-continuationbeen called. But nowcall-with-current-continuationyields a value, which isV. And the program continues.Let's take an example.
The first
displayoutput3, of cause.But the second
displayoutput2. Why?Let's dive into it.
When evaluating
(display (call-with-current-continuation f)), it will first evaluate(call-with-current-continuation f). We know that it will change the whole program toConsidering the definition for
f, it has a(return 2). We must evaluate(C 2). That's when thecontinuationbeing called. So it change the whole program back toBut now,
call-with-current-continuationhas value2. So the program becomes:Yin-Yang puzzle
Let's look at the puzzle.
Let's make it more readable.
Let's run the program in our brain.
Round 0
let*make us to evaluateyinfirst.yinisSo we evaluate
(call-with-current-continuation id)first. It packs the current environment, which we call itC_0to distinguish with other continuation in the time-line, and it enters a whole new universe:id. Butidjust returnsC_0.We should Remember what
C_0is.C_0is a program like this:###is a placeholder, which in the future will be filled by the value thatC_0takes back.But
idjust returnsC_0. It doesn't callC_0. If it calls, we will enterC_0's universe. But it didn't, so we continue to evaluateyin.fis a function likeid, but it has a side effect -- outputting@.So the program output
@and letyinto beC_0. Now the program becomesAfter
yinevaluated, we start to evaluateyang.yangiscall-with-current-continuationhere create another continuation, namedC_1.C_1is:###is placeholder. Note that in this continuation,yin's value is determined (that's whatlet*do). We are sure thatyin's value isC_0here.Since
(id C_1)isC_1, soyang's value isghas a side effect -- outputting*. So the program does.yang's value is nowC_1.By now, we have displayed
@*So now it becomes:
As both
yinandyangare solved, we should evaluate(yin yang). It'sHoly SH*T!
But finally,
C_0is called. So we fly into theC_0universe and forget all about these sh*ts. We will never go back to this universe again.Round 1
C_0take withC_1back. The program now becomes(If you forget whatC_0stands for, go back to see it):Ah, we find that
yin's value is not determined yet. So we evaluate it. In the process of evaluatingyin, we output an@asf's side effect. And we knowyinisC_1now.We begin to evaluate
yang, we came acrosscall-with-current-continuationagain. We are practiced. We create a continuationC_2which stands for:And we display a
*asgexecuting. And we come hereSo we got:
You know where we are going. We are going to
C_1's universe. We recall it from memory(or copy and paste from webpage). It is now:We know in
C_1's universe,yin's value has been determined. So we begin to evaluateyang. As we are practiced, I will directly tell you that it displays*and becomes:Now we have printed
@*@**, and we are going toC_0's universe taking withC_2.Round 2
As we are practiced, I will tell you that we display '@',
yinisC_2, and we create a new continuationC_3, which stands for:And we display
*,yangisC_3, and it becomesAnd we can continue. But I will stop here, I have showed you what Yin-Yang puzzle's first several outputs are.
Why the number of
*increases?Now your head is full of details. I will make a summary for you.
I will use a Haskell like syntax to simplify. And
ccis short forcall-with-current-continuation.When
#C_i#is bracketed by#, it means the continuation is create here.;means outputIf you observe carefully, it will be obvious to you that
C_0is the only universe that started byf. Others is started byg.C_0 C_nalways makes a new continuationC_max. It's becauseC_0is the first universe whichg cc idhas not been executed.C_0 C_nalso display@.C_n C_mwhich n is not 0 will display*.C_0 C_n, and I will prove thatC_0 C_nis separated by more and more other expression, which leads to@*@**@***...A little bit math
Assume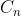 (n != 0) is the biggest numbered in all continuations, and then
(n != 0) is the biggest numbered in all continuations, and then
C_0 C_nis called.Assumption: When
C_0 C_nis called,C_nis the current maximum numbered continuation.Now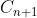 is created by
is created by
C_0 C_nlike this:So we conclude that:
Theorem I. If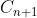 , in which
, in which
C_0 C_nis called, It will produce a continuationyinisC_n.Then next step is
C_n C_{n+1}.The reason why
yinisC_{n-1}is that WhenC_nbeing created it obeyed Theorem I.And then
C_{n-1} C_{n+1}is called, and we know whenC_{n-1}is created, it also obeyed Theorem I. So We haveC_{n-2} C_{n+1}.C_{n+1}is the in-variation. So we have the second theorem:Theorem II. If
C_n C_mwhichn < mandn > 0is called, It will becomeC_{n-1} C_m.And we have Manually checked
C_0C_1C_2C_3. They obey the Assumption and all Theorems. And we know how first@and*is created.So we can write patterns below.
It not so strict, but I'd like to write:
Q.E.D.
首先沉思,最后可能的答案。
我认为代码可以像这样重写:
或者使用一些额外的显示语句来帮助查看发生了什么:
或者像这样:
可能的答案
这可能不对,但我会尝试一下。
我认为关键点是“被调用”延续将堆栈返回到之前的某个状态 - 就好像没有其他东西一样发生了。它当然不知道我们通过显示
@和*字符来监控它。我们最初将
yin定义为一个延续A,它将执行以下操作:但是如果我们调用
yang延续,就会发生这种情况:We从这里开始。
第一次通过时,您会得到
yin=A和yang=B作为yin和yang> 正在初始化。(
A和B延续都会被计算。)现在
(yin yang)被评估为(AB)第一次。我们知道
A的作用。它执行以下操作:现在
(yin yang)被评估为(B B')。我们知道
B的作用。它的作用是:由于堆栈已恢复到
yin=A的位置,(yin yang)被评估为(A B')。我们知道
A的作用。它的作用是:我们知道
B'的作用。 :现在
(yin yang)被评估为(B B")。我们知道
B的作用。它执行以下操作:它执行以下操作 堆栈恢复到
yin=A、(yin yang)计算为(A B'")的位置。……
我想我们现在已经有了一个模式。
每次调用
(yin yang)时,我们都会循环遍历一堆B延续,直到回到yin=A并显示 <代码>@。我们循环遍历B延续堆栈,每次写入一个*。(如果这大致正确,我会非常高兴!)
谢谢你的提问。
Musings first, possible answer at the end.
I think the code can be re-written like this:
Or with some extra display statements to help see what is happening:
Or like this:
Possible Answer
This may not be right, but I'll have a go.
I think the key point is that a 'called' continuation returns the stack to some previous state - as if nothing else had happened. Of course it doesn't know that we monitoring it by displaying
@and*characters.We initially define
yinto be a continuationAthat will do this:But if we call a
yangcontinuation, this happens:We start here.
First time through you get
yin=Aandyang=Basyinandyangare being initialised.(Both
AandBcontinuations are computed.)Now
(yin yang)is evaluated as(A B)for the first time.We know what
Adoes. It does this:Now
(yin yang)is evaluated as(B B').We know what
Bdoes. It does this:Since the stack was restored to the point where
yin=A,(yin yang)is evaluated as(A B').We know what
Adoes. It does this:We know what
B'does. It does this:Now
(yin yang)is evaluated as(B B").We know what
Bdoes. It does this:Since the stack was restored to the point where
yin=A,(yin yang)is evaluated as(A B'")........
I think we have a pattern now.
Each time we call
(yin yang)we loop through a stack ofBcontinuations until we get back to whenyin=Aand we display@. The we loop through the stack ofBcontinuations writing a*each time.(I'd be really happy if this is roughly right!)
Thanks for the question.