有障碍物的 2D 包装
有人知道在包含障碍物的正方形中移动矩形的有效算法吗?
矩形:
- 可以旋转
- 可以移动/传送
- 不能与障碍物碰撞(黑色方块)
障碍物:
- 不能移动
- 可以添加到任何地方
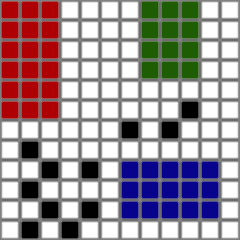
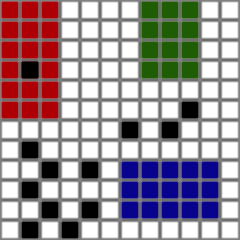
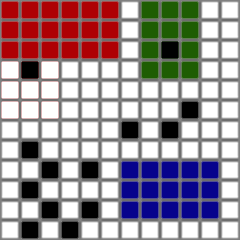
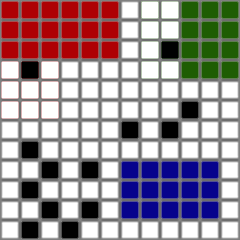
目标:添加障碍物时,尝试移动矩形,使其不会与任何障碍物碰撞。
Anybody know of an efficient algorithm for moving rectangles in a square which contains obstacles?
Rectangles:
- can rotate
- can move/teleport
- must not collide with obstacles (black squares)
Obstacles:
- can't be moved
- can be added anywhere
Goal: when obstacle is added, try to move rectangles so that they don't collide with any of obstacles.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(1)
看看这个:动态规划 - 最大方块
基本上,给定矩形,您添加一个障碍物,并删除障碍物干扰的正方形。
然后,运行链接算法(“限制器”是障碍物和现有正方形),如果找到可以容纳 NxN 大小的正方形(N 是矩形的大部分)的位置,则添加矩形) .
这可以进一步优化,我委托你这样做。 (基本上 - 矩形并不总是被放置在最佳位置。这是可以补救的,至少在某种程度上)
此解决方案将为您添加的每个障碍提供 O(n) 时间和空间。
您还应该考虑可能的修改:不要为每个障碍物重建数组,而是为无障碍物数组构建它,并在进行过程中对其进行修改。这将节省针对每个障碍物遍历整个阵列的时间。
Take a look at this: Dynamic programming - Largest square block
Basically, given the rectangles, you add an obstacle, and remove the square that the obstacle interferes with.
Then, run the linked algorithm(with the "limiters" being the obstacles and existing squares), and if a place was found that can fit a square of NxN size (N is the large part of the rectangle), and add the rectangle).
This can be optimized a bit further, and I entrust you with doing so. (Basically - the rectangles won't always be put in the most optimal place. This can be remedied, at least to some degree)
This solution will give you O(n) time and space for each obstacle added.
Possible modification you should also look into: Don't rebuild the array for each obstacle, but build it for the void-of-obstacles array, and modify it as you go along. This will save going through the entire array for every single obstacle.