计算 3D 平面多边形的质心
This is a similar question to this one here.
Given a list of 3D coordinates that define the surface( Point3D1, Point3D2, Point3D3, and so on), how to calculate the centroid of the surface?
In 2D the computation is given by the following formula:

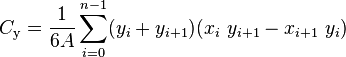
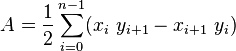
What about the 3D analogue?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!



发布评论
评论(3)
只需使用两次方程式,但第二次将 z 替换为 y。
也就是说,计算两个投影的质心,一个投影到 xy 平面上,另一个投影到 xz 平面上。投影的质心将是实际质心的投影,因此答案将是您找到的 x、y 和 z 值这两个计算。
更明确地说:如果您的点是 (x1, y1, z1), (x2, y2, z2),... ,要获得 xy 质心 (Cx, Cy),请使用 (x1, y1) 进行计算, (x2, y2),... 并获得 xz 质心,(Cx, Cz) 使用点 (x1, z1), (x2, z2),.... - 只需使用相同的值进行第二次计算2D 公式,将 z 值视为方程中的 y。那么您的 3D 质心将为 (Cx, Cy, Cz)。只要表面平坦且不平行于 xy、xz 或 yz 平面(但如果平行,则只是二维方程),此方法就有效。
Just use the equations that you have twice, but the second time swap in z for y.
That is, calculate the centroids of the two projections, one onto the x-y plane, and the other onto the x-z plane. The centroids of the projections will be projections of the actual centroid, so the answer will be the x, y, and z values you find from these two calculations.
Stated more explicitly: If your points are (x1, y1, z1), (x2, y2, z2),... , to get the x-y centroid, (Cx, Cy), do a calculation using (x1, y1), (x2, y2),... and to get the x-z centroid, (Cx, Cz) use the points (x1, z1), (x2, z2),.... -- just do the second calculation with your same 2D formula, treating the z values as the y in the equation. Then your 3D centroid will be (Cx, Cy, Cz). This will work as long as your surface is flat and isn't parallel to the x-y, x-z, or y-z planes (but if it is parallel it's just the 2D equation).
设逆时针方向的点为 v0, v1, ..., vN,其中 vi = (xi, yi, zi).
然后是三元组 (v0, v1, v2), (v0, v 2, v3), ..., (v0, vi, vi+1< /sub>), ..., (v0, vN-1, vN) 形成 N-1 个三角形,从而创建多边形。
每个三角形的面积为| (vi - v0) × (vi+1 - v0) | ÷ 2,其中 × 是叉积,| · |是向量长度。
您可能需要将面积设置为负数以补偿凹陷部分。一个简单的检查是计算 (vi − v0) × (vi+1 − v0< /sub>) · (v1 - v0) × (v2 - v0).该区域应具有与结果相同的符号。
由于平行投影下二维图形的面积比是恒定的,因此您可能需要选择不平行于平面的单位向量(例如 z),即 (vi − v0) × (vi+1 − v0) · z 为面积。这样,您就不需要执行昂贵的平方根,并且符号检查会自动完成。
每个三角形的质心为 (v0 + vi + vi+1) ÷ 3。
因此,假设密度均匀,整个多边形的质心为
(对于尺寸 ≥ 4D,需要使用 Ai = ½ |vi−v 计算面积0| vi+1−v0| sin θi,其中 cos θi = (vi−v0) · (vi+1−v0) )
Let the points be v0, v1, ..., vN in counterclockwise, where vi = (xi, yi, zi).
Then the triplets (v0, v1, v2), (v0, v2, v3), ..., (v0, vi, vi+1), ..., (v0, vN-1, vN) forms N-1 triangles that create the polygon.
The area of each triangle is | (vi − v0) × (vi+1 − v0) | ÷ 2, where × is the cross product and | · | is vector length.
You may need to make the area negative to compensate for concave parts. A simple check is to compute (vi − v0) × (vi+1 − v0) · (v1 − v0) × (v2 − v0). The area should have the same sign as the result.
Since ratio of area of 2D figures is constant under parallel projection, you may want to choose a unit vector (e.g. z) not parallel to the plane, the treat (vi − v0) × (vi+1 − v0) · z as the area. With this, you don't need to perform the expensive square root, and the sign check is automatically taken care of.
The centroid of each triangle is (v0 + vi + vi+1) ÷ 3.
Hence, the centroid of the whole polygon is, assuming uniform density,
(For dimensions ≥ 4D, the area needs to be computed with Ai = ½ |vi−v0| |vi+1−v0| sin θi, where cos θi = (vi−v0) · (vi+1−v0). )
如果它是平面,您可以转换为该平面的局部坐标系,使用您提供的公式计算质心,然后转换回来以获得其在 3D 空间中的坐标。
If it's a planar surface, you can transform to a coordinate system local to the plane, calculate the centroid using the formulas you presented, and then transform back to get its coordinates in 3D space.