如何计算单个点质量?
我正在开发 C# 2d 软体物理引擎,我需要将质量分配给给定的对象顶点:顶点列表(x,y 位置)、对象的总质量和质心。
质心给出为:
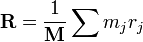
其中,
R = center of mass
M = total mass
mj = mass of vertex j
rj = position of vertex j
我需要一个可以给定 R、M 和 rj 来近似每个 mj。
编辑:我只是想澄清一下,我知道有无限的解决方案。我正在寻找一种快速算法,可以找到一组 mj (使得它们每个都足够接近 mj = M/[顶点数],并且其中“足够”被定义为一些小的浮点阈值)。
此外,每个对象将由大约 5 到 35 个点组成。
I am working on a C# 2d soft body physics engine and I need to assign masses to an object's vertices given: a list of vertices (x,y positions), the total mass for the object, and the center of mass.
The center of mass is given as:
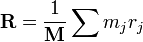
where,
R = center of mass
M = total mass
mj = mass of vertex j
rj = position of vertex j
I need an algorithm that can approximate each mj given R, M, and rj.
edit: I just want to clarify that I am aware that there are an infinite set of solutions. I am looking for a quick algorithm that finds a set of mj's (such that they are each sufficiently close to mj = M/[number of vertices] and where "sufficiently" is defined as some small floating point threshold).
Also, each object will consist of about 5 to 35 points.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!


发布评论
评论(4)
您可以按如下方式计算均匀密集多边形的 CM:从 0..N-1 对 N 个顶点进行编号,并循环处理它们,以便顶点 N 环绕到顶点 0:
如果多边形是凸多边形,则 CM 将在内部多边形,因此您可以合理地将区域像饼图一样切成三角形,以 CM 为中心。您应该能够用其质量的三分之一来对三角形的每个顶点进行加权,而不更改 CM - 但是,这仍然会在整个多边形的 CM 处留下总质量的三分之一。尽管如此,将质量传递缩放 3/2 应该可以让您将每个三角形的质量分割到两个“外部”顶点之间。因此,
请注意,这种质量传递是完全“非物理的”——如果不出意外,如果按字面意思处理,它会严重破坏惯性矩。但是,如果您需要在顶点之间分配质量(例如某种俗气的爆炸),并且您不想在这样做时破坏 CM,那么这应该可以解决问题。
最后,有几个警告:
You can compute the CM of a uniformly dense polygon as follows: number the N vertices from 0..N-1, and treat them cyclicly, so that vertex N wraps to vertex 0:
If the polygon is convex, the CM will be inside the polygon, so you can reasonably start out by slicing up the area in triangles like a pie, with the CM at the hub. You should be able to weight each vertex of a triangle with a third of its mass, without changing the CM -- however, this would still leave a third of the total mass at the CM of the entire polygon. Nonetheless, scaling the mass transfer by 3/2 should let you split the mass of each triangle between the two "external" vertices. As a result,
Note that this kind of mass transfer is profoundly "unphysical" -- if nothing else, if treated literally, it would screw up the moment of inertia something fierce. However, if you need to distribute the mass among the vertices (like for some kind of cheesy explosion), and you don't want to disrupt the CM in doing so, this should do the trick.
Finally, a couple of warnings:
随着顶点的移动,质心 R 会不断变化。因此,如果您有 10 个顶点,请存储 10 个连续“帧”的值 - 这将为您提供 10 个未知数的 10 个方程(假设质量不随时间变化)。
The center of mass R will constantly be changing as the vertices move. So, if you have 10 vertices, store the values from 10 consecutive "frames" - this will give you 10 equations for your 10 unknowns (assuming that the masses don't change over time).
计算自由度:对于
D维空间中的点,您有D+1方程[+] 和n未知数n分离粒子。如果n>D+1你就沉没了(除非你有比你告诉我们的更多的信息:对称约束、高阶矩等......)。编辑:我的早期版本假设您拥有
m_i并正在寻找r_i。当您拥有r_i并想要m_i时,情况会稍微好一些。[+] 你上面列出的那个(实际上是
D单独的方程)和M = \sum m_jArriu说:
现在我们已经取得进展了。你确实知道更多的东西。
您可以通过将对象分成相邻点之间的三角形来估算对象的表面积。这个总面积给出了平均质量密度。现在找到 DoF 赤字,并根据平均密度和它所属的每个三角形面积的 1/3 为许多 r_i(我猜是随机绘制的)分配一个初始质量。然后解析求解剩余系统。如果问题是病态的,您可以绘制一组新的指定点,或者尝试对您已经猜测的群众进行随机游走。
Count the degrees of freedom: for points in
Ddimensional space you haveD+1equations[+] andnunknowns fornseparate particles. Ifn>D+1you are sunk (unless you have more information than you have told us about: symmetry constraints, higher order moments, etc...).edit: My earlier version assumed you had the
m_is and were looking for ther_is. It is slightly better when you have ther_is and want them_is.[+] The one you list above (which is actual
Dseparate equation) andM = \sum m_jArriu said:
Now we are getting somewhere. You do know something more.
You can approximate the surface area of the object by breaking it into triangles between adjacent points. This total area gives you mean mass density. Now find the DoF deficit, and assign that many
r_is (drawn at random, I guess) an initial mass based on the mean density and 1/3 of the area of each triangle it is a party to. Then solve the remaining system analytically. If the problem is ill-conditioned you can either draw a new set of assigned points, or attempt a random walk on the masses that you have already guessed at.我会扭转这个问题。也就是说,给定物体的密度和位置(当然自然仍然是物体的质心和与物体的方向相对应的三个向量,请参见欧拉角),在每个顶点处将一个体积与该体积相关联元素(会随分辨率而变化,并且对于物体边缘的位置可能是小数)并将密度 (d_j) 与相关体积 (v_j) 相乘,m_j=v_j * d_j。这种方法应该自然地再次再现物体的质心。
也许我不明白你的问题,但考虑到这最终会产生正确的质量( Mass = sum(m_j) = sum(v_j * d_j) ),最坏的情况是这种方法应该产生对你的结果的验证。
I would flip the problem around. That is, given a density and the position of the object (which is of course naturally still the center of mass of the object and three vectors corresponding to the orientation of the object, see Euler's angles), at each vertex associate a volume with that element (which would change with resolution and could be fractional for positions at the edge of the object) and multiply the density (d_j) with the associated volume (v_j), m_j=v_j * d_j. This approach should naturally reproduce the center of the mass of the object again.
Perhaps I didn't understand your problem, but consider that this would ultimately yield the correct mass ( Mass = sum(m_j) = sum(v_j * d_j) ) and at worst this approach should yield a verification of your result.